
History of quaternions
Encyclopedia
In mathematics
, quaternion
s are a non-commutative
number system that extends the complex numbers. Quaternions and their applications to rotations were first described in print by Olinde Rodrigues
in all but name in 1840, but independently discovered by Irish mathematician Sir William Rowan Hamilton
in 1843 and applied to mechanics in three-dimensional space. They find uses in both theoretical and applied mathematics, in particular for calculations involving three-dimensional rotations. This article describes the original invention and subsequent development of quaternions.
s could be viewed as point
s in a plane
and that they could be added and multiplied together using certain geometric operations. Hamilton sought to find a way to do the same for points in space
. Points in space can be represented by their coordinates, which are triples of numbers and have an obvious addition, but Hamilton had been stuck on defining the appropriate multiplication.
According to a letter Hamilton wrote later to his son Archibad:
On October 16, 1843, Hamilton and his wife took a walk along the Royal Canal in Dublin. While they walked across Brougham Bridge (now Broom Bridge
), a solution suddenly occurred to him. While he could not "multiply triples", he saw a way to do so for quadruples. By using three of the numbers in the quadruple as the points of a coordinate in space, Hamilton could represent points in space by his new system of numbers. He then carved the basic rules for multiplication into the bridge: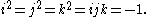
Hamilton called a quadruple with these rules of multiplication a quaternion, and he devoted the remainder of his life to studying and teaching them. He founded a school of "quaternionists" and popularized them in several books. The last and longest, Elements of Quaternions, had 800 pages and was published shortly after his death. See "classical Hamiltonian quaternions
" for a summary of Hamilton's work.
applied this formula to representing rotations in 1840.
, as well as Benjamin Peirce
, continued advocating the use of quaternions. Topics in physics and geometry that would now be described using vectors, such as kinematics
in space and Maxwell's equations
, were described entirely in terms of quaternions. There was a professional research association which existed from 1899 to 1913, the Quaternion Society, exclusively devoted to the study of quaternions.
From the mid 1880s, quaternions began to be displaced by vector analysis, which had been developed by Josiah Willard Gibbs
and Oliver Heaviside
. Both were inspired by the quaternions as used in Maxwell's A Treatise on Electricity and Magnetism
, but — according to Gibbs — found that "… the idea of the quaternion was quite foreign to the subject." Vector analysis described the same phenomena as quaternions, so it borrowed ideas and terms liberally from the classical quaternion literature. However, vector analysis was conceptually simpler and notationally cleaner, and eventually quaternions were relegated to a minor role in mathematics and physics. A side effect of this transition is that works on classical Hamiltonian quaternions
are difficult to comprehend for many modern readers because they use familiar terms from vector analysis in unfamiliar and fundamentally different ways.
s were developed independently by Arthur Cayley
in 1845 and John T. Graves
, a friend of Hamilton's. Graves had interested Hamilton in algebra, and responded to his discovery of quaternions with "If with your alchemy you can make three pounds of gold [the three imaginary units], why should you stop there?"
Two months after Hamilton's discovery of quaternions, Graves wrote Hamilton on December 26, 1843 presenting a kind of double quaternion that is now days often called an octonion, and showing that they were what we now call norm
ed division algebra
; Graves called them octaves. Hamilton needed a way to distinguish between two different types of double quaternions, the associative bi-quaternions and the octaves. He spoke about them to the Royal Irish Society and credited his friend Graves for the discovery of the second type of double quaternion. observed in reply that they were not associative
, which may have been the invention of the concept. He also promised to get Graves' work published, but did little about it; Cayley, working independently of Graves, but inspired by Hamilton's publication of his own work, published on octonions in March 1845 – as an appendix to a paper on a different subject. Hamilton was stung into protesting Graves' priority in discovery, if not publication; nevertheless, octonions are known by the name Cayley gave them – or as Cayley numbers.
The major deduction from the existence of octonions was the eight squares theorem
, which follows directly from the product rule from octonions, had also been previously discovered as a purely algebraic identity, by Ferdinand Degen in 1818.
systems over the reals, followed by the octonion
s and the sedenion
s; they are also useful tool in number theory
, particularly in the study of the representation of numbers as sums of squares. The group of eight basic unit quaternions, positive and negative, the quaternion group
, is also the simplest non-commutative Sylow group.
The study of integral quaternions began with Rudolf Lipschitz
in 1886, whose system was later simplified by Leonard Eugene Dickson
; but the modern system was published by Adolf Hurwitz
in 1919. The difference between them consists of which quaternions are accounted integral: Lipschitz included only those quaternions with integral coordinates, but Hurwitz added those quaternions all four of whose coordinates are half-integers. Both systems are closed under subtraction and multiplication, and are therefore ring
s, but Lipschitz's system does not permit unique factorization, while Hurwitz's does.
s of three- and four-dimensional spaces. They have the technical advantage that unit quaternions form the simply connected cover of the space of three-dimensional rotations.
For this reason, quaternions are used in computer graphics
, control theory
, signal processing
, attitude control, physics
, bioinformatics
, and orbital mechanics. For example, it is common for spacecraft attitude-control systems to be commanded in terms of quaternions. Tomb Raider
(1996) is often cited as the first mass-market computer game to have used quaternions to achieve smooth 3D rotation. Quaternions have received another boost from number theory
because of their relation to quadratic form
s.
has organized a pilgrimage, where scientists (including physicists Murray Gell-Mann
in 2002, Steven Weinberg
in 2005, Frank Wilczek
in 2007, and mathematician Andrew Wiles
in 2003) take a walk from Dunsink Observatory
to the Royal Canal bridge where, unfortunately, no trace of Hamilton's carving remains.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, quaternion
Quaternion
In mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
s are a non-commutative
Commutativity
In mathematics an operation is commutative if changing the order of the operands does not change the end result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it...
number system that extends the complex numbers. Quaternions and their applications to rotations were first described in print by Olinde Rodrigues
Olinde Rodrigues
Benjamin Olinde Rodrigues , more commonly known as Olinde Rodrigues, was a French banker, mathematician, and social reformer.Rodrigues was born into a well-to-do Sephardi Jewish family in Bordeaux....
in all but name in 1840, but independently discovered by Irish mathematician Sir William Rowan Hamilton
William Rowan Hamilton
Sir William Rowan Hamilton was an Irish physicist, astronomer, and mathematician, who made important contributions to classical mechanics, optics, and algebra. His studies of mechanical and optical systems led him to discover new mathematical concepts and techniques...
in 1843 and applied to mechanics in three-dimensional space. They find uses in both theoretical and applied mathematics, in particular for calculations involving three-dimensional rotations. This article describes the original invention and subsequent development of quaternions.
Hamilton's discovery
In 1843, Hamilton knew that the complex numberComplex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s could be viewed as point
Point (geometry)
In geometry, topology and related branches of mathematics a spatial point is a primitive notion upon which other concepts may be defined. In geometry, points are zero-dimensional; i.e., they do not have volume, area, length, or any other higher-dimensional analogue. In branches of mathematics...
s in a plane
Plane (mathematics)
In mathematics, a plane is a flat, two-dimensional surface. A plane is the two dimensional analogue of a point , a line and a space...
and that they could be added and multiplied together using certain geometric operations. Hamilton sought to find a way to do the same for points in space
Space
Space is the boundless, three-dimensional extent in which objects and events occur and have relative position and direction. Physical space is often conceived in three linear dimensions, although modern physicists usually consider it, with time, to be part of a boundless four-dimensional continuum...
. Points in space can be represented by their coordinates, which are triples of numbers and have an obvious addition, but Hamilton had been stuck on defining the appropriate multiplication.
According to a letter Hamilton wrote later to his son Archibad:
Every morning in the early part of October 1843, on my coming down to breakfast, your brother William Edward and yourself used to ask me: "Well, Papa, can you multiply triples?" Whereto I was always obliged to reply, with a sad shake of the head, "No, I can only add and subtract them."
On October 16, 1843, Hamilton and his wife took a walk along the Royal Canal in Dublin. While they walked across Brougham Bridge (now Broom Bridge
Broom Bridge
Broom Bridge, also known as Brougham Bridge, is a bridge along Broombridge Road which crosses the Royal Canal in Cabra, Dublin, Ireland. Broom Bridge is named after William Brougham, one of the directors of the Royal Canal company...
), a solution suddenly occurred to him. While he could not "multiply triples", he saw a way to do so for quadruples. By using three of the numbers in the quadruple as the points of a coordinate in space, Hamilton could represent points in space by his new system of numbers. He then carved the basic rules for multiplication into the bridge:
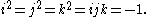
Hamilton called a quadruple with these rules of multiplication a quaternion, and he devoted the remainder of his life to studying and teaching them. He founded a school of "quaternionists" and popularized them in several books. The last and longest, Elements of Quaternions, had 800 pages and was published shortly after his death. See "classical Hamiltonian quaternions
Classical Hamiltonian quaternions
William Rowan Hamilton invented quaternions, a mathematical entity in 1843. This article describes Hamilton's original treatment of quaternions, using his notation and terms. Hamilton's treatment is more geometric than the modern approach, which emphasizes quaternions' algebraic properties...
" for a summary of Hamilton's work.
Precursors
Hamilton's innovation consisted of expressing quaternions as an algebra. The formulae for the multiplication of quaternions are implicit in the four squares formula devised by Leonard Euler in 1748; Olinde RodriguesOlinde Rodrigues
Benjamin Olinde Rodrigues , more commonly known as Olinde Rodrigues, was a French banker, mathematician, and social reformer.Rodrigues was born into a well-to-do Sephardi Jewish family in Bordeaux....
applied this formula to representing rotations in 1840.
After Hamilton
After Hamilton's death, his pupil Peter TaitPeter Guthrie Tait
Peter Guthrie Tait FRSE was a Scottish mathematical physicist, best known for the seminal energy physics textbook Treatise on Natural Philosophy, which he co-wrote with Kelvin, and his early investigations into knot theory, which contributed to the eventual formation of topology as a mathematical...
, as well as Benjamin Peirce
Benjamin Peirce
Benjamin Peirce was an American mathematician who taught at Harvard University for approximately 50 years. He made contributions to celestial mechanics, statistics, number theory, algebra, and the philosophy of mathematics....
, continued advocating the use of quaternions. Topics in physics and geometry that would now be described using vectors, such as kinematics
Kinematics
Kinematics is the branch of classical mechanics that describes the motion of bodies and systems without consideration of the forces that cause the motion....
in space and Maxwell's equations
Maxwell's equations
Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
, were described entirely in terms of quaternions. There was a professional research association which existed from 1899 to 1913, the Quaternion Society, exclusively devoted to the study of quaternions.
From the mid 1880s, quaternions began to be displaced by vector analysis, which had been developed by Josiah Willard Gibbs
Josiah Willard Gibbs
Josiah Willard Gibbs was an American theoretical physicist, chemist, and mathematician. He devised much of the theoretical foundation for chemical thermodynamics as well as physical chemistry. As a mathematician, he invented vector analysis . Yale University awarded Gibbs the first American Ph.D...
and Oliver Heaviside
Oliver Heaviside
Oliver Heaviside was a self-taught English electrical engineer, mathematician, and physicist who adapted complex numbers to the study of electrical circuits, invented mathematical techniques to the solution of differential equations , reformulated Maxwell's field equations in terms of electric and...
. Both were inspired by the quaternions as used in Maxwell's A Treatise on Electricity and Magnetism
A Treatise on Electricity and Magnetism
A Treatise on Electricity and Magnetism is a two volume treatise on electromagnetism written by James Clerk Maxwell in 1873.-See also:* On Physical Lines of Force* A Dynamical Theory of the Electromagnetic Field-External links:...
, but — according to Gibbs — found that "… the idea of the quaternion was quite foreign to the subject." Vector analysis described the same phenomena as quaternions, so it borrowed ideas and terms liberally from the classical quaternion literature. However, vector analysis was conceptually simpler and notationally cleaner, and eventually quaternions were relegated to a minor role in mathematics and physics. A side effect of this transition is that works on classical Hamiltonian quaternions
Classical Hamiltonian quaternions
William Rowan Hamilton invented quaternions, a mathematical entity in 1843. This article describes Hamilton's original treatment of quaternions, using his notation and terms. Hamilton's treatment is more geometric than the modern approach, which emphasizes quaternions' algebraic properties...
are difficult to comprehend for many modern readers because they use familiar terms from vector analysis in unfamiliar and fundamentally different ways.
Octonions
OctonionOctonion
In mathematics, the octonions are a normed division algebra over the real numbers, usually represented by the capital letter O, using boldface O or blackboard bold \mathbb O. There are only four such algebras, the other three being the real numbers R, the complex numbers C, and the quaternions H...
s were developed independently by Arthur Cayley
Arthur Cayley
Arthur Cayley F.R.S. was a British mathematician. He helped found the modern British school of pure mathematics....
in 1845 and John T. Graves
John T. Graves
John Thomas Graves was an Irish jurist and mathematician. He was a friend of William Rowan Hamilton, and is credited both with inspiring Hamilton to discover the quaternions and with personally discovering the octonions, which he called the octaves...
, a friend of Hamilton's. Graves had interested Hamilton in algebra, and responded to his discovery of quaternions with "If with your alchemy you can make three pounds of gold [the three imaginary units], why should you stop there?"
Two months after Hamilton's discovery of quaternions, Graves wrote Hamilton on December 26, 1843 presenting a kind of double quaternion that is now days often called an octonion, and showing that they were what we now call norm
Norm (mathematics)
In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
ed division algebra
Division algebra
In the field of mathematics called abstract algebra, a division algebra is, roughly speaking, an algebra over a field, in which division is possible.- Definitions :...
; Graves called them octaves. Hamilton needed a way to distinguish between two different types of double quaternions, the associative bi-quaternions and the octaves. He spoke about them to the Royal Irish Society and credited his friend Graves for the discovery of the second type of double quaternion. observed in reply that they were not associative
Associativity
In mathematics, associativity is a property of some binary operations. It means that, within an expression containing two or more occurrences in a row of the same associative operator, the order in which the operations are performed does not matter as long as the sequence of the operands is not...
, which may have been the invention of the concept. He also promised to get Graves' work published, but did little about it; Cayley, working independently of Graves, but inspired by Hamilton's publication of his own work, published on octonions in March 1845 – as an appendix to a paper on a different subject. Hamilton was stung into protesting Graves' priority in discovery, if not publication; nevertheless, octonions are known by the name Cayley gave them – or as Cayley numbers.
The major deduction from the existence of octonions was the eight squares theorem
Degen's eight-square identity
In mathematics, Degen's eight-square identity establishes that the product of two numbers, each of which being a sum of eight squares, is itself a sum of eight squares...
, which follows directly from the product rule from octonions, had also been previously discovered as a purely algebraic identity, by Ferdinand Degen in 1818.
Mathematical uses
Quaternions continued to be a well-studied mathematical structure in the twentieth century, as the third term in the Cayley–Dickson construction of hypercomplex numberHypercomplex number
In mathematics, a hypercomplex number is a traditional term for an element of an algebra over a field where the field is the real numbers or the complex numbers. In the nineteenth century number systems called quaternions, tessarines, coquaternions, biquaternions, and octonions became established...
systems over the reals, followed by the octonion
Octonion
In mathematics, the octonions are a normed division algebra over the real numbers, usually represented by the capital letter O, using boldface O or blackboard bold \mathbb O. There are only four such algebras, the other three being the real numbers R, the complex numbers C, and the quaternions H...
s and the sedenion
Sedenion
In abstract algebra, sedenions form a 16-dimensional non-associative algebra over the reals obtained by applying the Cayley–Dickson construction to the octonions...
s; they are also useful tool in number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, particularly in the study of the representation of numbers as sums of squares. The group of eight basic unit quaternions, positive and negative, the quaternion group
Quaternion group
In group theory, the quaternion group is a non-abelian group of order eight, isomorphic to a certain eight-element subset of the quaternions under multiplication...
, is also the simplest non-commutative Sylow group.
The study of integral quaternions began with Rudolf Lipschitz
Rudolf Lipschitz
Rudolf Otto Sigismund Lipschitz was a German mathematician and professor at the University of Bonn from 1864. Peter Gustav Dirichlet was his teacher. He supervised the early work of Felix Klein....
in 1886, whose system was later simplified by Leonard Eugene Dickson
Leonard Eugene Dickson
Leonard Eugene Dickson was an American mathematician. He was one of the first American researchers in abstract algebra, in particular the theory of finite fields and classical groups, and is also remembered for a three-volume history of number theory.-Life:Dickson considered himself a Texan by...
; but the modern system was published by Adolf Hurwitz
Adolf Hurwitz
Adolf Hurwitz was a German mathematician.-Early life:He was born to a Jewish family in Hildesheim, former Kingdom of Hannover, now Lower Saxony, Germany, and died in Zürich, in Switzerland. Family records indicate that he had siblings and cousins, but their names have yet to be confirmed...
in 1919. The difference between them consists of which quaternions are accounted integral: Lipschitz included only those quaternions with integral coordinates, but Hurwitz added those quaternions all four of whose coordinates are half-integers. Both systems are closed under subtraction and multiplication, and are therefore ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
s, but Lipschitz's system does not permit unique factorization, while Hurwitz's does.
Quaternions as rotations
Quaternions are a concise method of representing the automorphismAutomorphism
In mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism...
s of three- and four-dimensional spaces. They have the technical advantage that unit quaternions form the simply connected cover of the space of three-dimensional rotations.
For this reason, quaternions are used in computer graphics
Computer graphics
Computer graphics are graphics created using computers and, more generally, the representation and manipulation of image data by a computer with help from specialized software and hardware....
, control theory
Control theory
Control theory is an interdisciplinary branch of engineering and mathematics that deals with the behavior of dynamical systems. The desired output of a system is called the reference...
, signal processing
Signal processing
Signal processing is an area of systems engineering, electrical engineering and applied mathematics that deals with operations on or analysis of signals, in either discrete or continuous time...
, attitude control, physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, bioinformatics
Bioinformatics
Bioinformatics is the application of computer science and information technology to the field of biology and medicine. Bioinformatics deals with algorithms, databases and information systems, web technologies, artificial intelligence and soft computing, information and computation theory, software...
, and orbital mechanics. For example, it is common for spacecraft attitude-control systems to be commanded in terms of quaternions. Tomb Raider
Tomb Raider
Tomb Raider is an action-adventure video game developed by Core Design and published by Eidos Interactive. It was originally released in 1996 for the Sega Saturn, with MS-DOS and PlayStation versions following shortly thereafter...
(1996) is often cited as the first mass-market computer game to have used quaternions to achieve smooth 3D rotation. Quaternions have received another boost from number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
because of their relation to quadratic form
Quadratic form
In mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....
s.
Memorial
Since 1989, the Department of Mathematics of the National University of Ireland, MaynoothNational University of Ireland, Maynooth
The National University of Ireland, Maynooth , was founded by the Universities Act, 1997 as a constituent university of the National University of Ireland. It is Ireland's second oldest university, having been formed from St Patrick's College, Maynooth, itself founded in 1795.The university is...
has organized a pilgrimage, where scientists (including physicists Murray Gell-Mann
Murray Gell-Mann
Murray Gell-Mann is an American physicist and linguist who received the 1969 Nobel Prize in physics for his work on the theory of elementary particles...
in 2002, Steven Weinberg
Steven Weinberg
Steven Weinberg is an American theoretical physicist and Nobel laureate in Physics for his contributions with Abdus Salam and Sheldon Glashow to the unification of the weak force and electromagnetic interaction between elementary particles....
in 2005, Frank Wilczek
Frank Wilczek
Frank Anthony Wilczek is a theoretical physicist from the United States and a Nobel laureate. He is currently the Herman Feshbach Professor of Physics at the Massachusetts Institute of Technology ....
in 2007, and mathematician Andrew Wiles
Andrew Wiles
Sir Andrew John Wiles KBE FRS is a British mathematician and a Royal Society Research Professor at Oxford University, specializing in number theory...
in 2003) take a walk from Dunsink Observatory
Dunsink Observatory
The Dunsink Observatory is an astronomical observatory established in 1785 in the townland of Dunsink near the city of Dublin, Ireland.Its most famous director was William Rowan Hamilton, who, amongst other things, discovered quaternions, the first non-commutative algebra, while strolling from the...
to the Royal Canal bridge where, unfortunately, no trace of Hamilton's carving remains.

