In mathematics

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, a tubular neighborhood of a submanifold

Submanifold

In mathematics, a submanifold of a manifold M is a subset S which itself has the structure of a manifold, and for which the inclusion map S → M satisfies certain properties. There are different types of submanifolds depending on exactly which properties are required...

 of a smooth manifold is an open set

Open set

The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...

 around it resembling the normal bundle

Normal bundle

In differential geometry, a field of mathematics, a normal bundle is a particular kind of vector bundle, complementary to the tangent bundle, and coming from an embedding .-Riemannian manifold:...

.

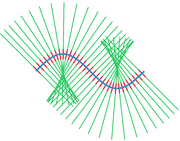
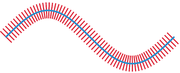
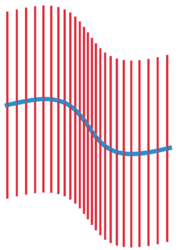
The idea behind a tubular neighborhood can be explained in a simple example. Consider a smooth curve in the plane without self-intersections. On each point on the curve draw a line perpendicular to the curve. Unless the curve is straight, these lines will intersect among themselves in a rather complicated fashion. However, if one looks only in a narrow band around the curve, the portions of the lines in that band will not intersect, and will cover the entire band without gaps. This band is the tubular neighborhood.

In general, let S be a submanifold

Submanifold

In mathematics, a submanifold of a manifold M is a subset S which itself has the structure of a manifold, and for which the inclusion map S → M satisfies certain properties. There are different types of submanifolds depending on exactly which properties are required...

 of a manifold

Manifold

In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....

 M, and let N be the normal bundle

Normal bundle

In differential geometry, a field of mathematics, a normal bundle is a particular kind of vector bundle, complementary to the tangent bundle, and coming from an embedding .-Riemannian manifold:...

 of S in M. Here S plays the role of the curve and M the role of the plane containing the curve. Consider the natural map
which establishes a bijective correspondence between the zero section N₀ of N and the submanifold S of M. An extension j of this map to the entire normal bundle N with values in M such that j(N) is an open set in M and j is a homeomorphism between N and j(N) is called a tubular neighbourhood.

Often one calls the open set T=j(N), rather than j itself, a tubular neighbourhood of S, it is assumed implicitly that the homeomorphism j mapping N to T exists.

Generalizations

Generalizations of smooth manifolds yield generalizations of tubular neighborhoods, such as regular neighborhoods, or spherical fibrations for Poincaré space

Poincaré space

In algebraic topology, a Poincaré space is an n-dimensional topological space with a distinguished element µ of its nth homology group such that taking the cap product with an element of the kth cohomology group yields an isomorphism to the th cohomology group...

s.

These generalizations are used to produce analogs to the normal bundle, or rather to the stable normal bundle

Stable normal bundle

In surgery theory, a branch of mathematics, the stable normal bundle of a differentiable manifold is an invariant which encodes the stable normal data. There are analogs for generalizations of manifold, notably PL-manifolds and topological manifolds...

, which are replacements for the tangent bundle (which does not admit a direct description for these spaces).