Cerf theory
Encyclopedia
In mathematics
, at the junction of singularity theory
and differential topology
, Cerf theory is the study of families of smooth real-valued functions
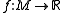
on a smooth manifold M, their generic singularities and the topology of the subspaces these singularities define, as subspaces of the function space.
proved that, provided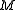
is compact, any smooth function
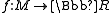
could be approximated by a Morse function
. So for many purposes, one can replace arbitrary functions on
by Morse functions.
As a next step, one could ask, 'if you have a 1-parameter family of functions which start and end at Morse functions, can you assume the whole family is Morse?' In general the answer is no. Consider, for example, the family:
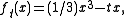
as a 1-parameter family of functions on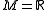
.
At time
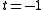
it has no critical points, but at time
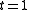
it is a Morse function with two critical points
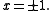
Jean Cerf showed that a 1-parameter family of functions between two Morse functions could be approximated by one that is Morse at all but finitely many degenerate times. The degeneracies involve a birth/death transition of critical points, as in the above example when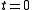
an index 0 and index 1 critical point are created (as 
increases).
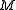is a compact manifold.
Let
denote the space of Morse functions
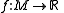
and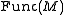
the space of smooth functions
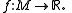
Morse proved that
is an open and dense subset in the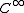
topology.
For the purposes of intuition, here is an analogy. Think of the Morse functions as the top-dimensional open stratum in a stratification
of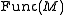
(we make no claim that such a stratification exists, but suppose one does). Notice that in stratified spaces, the co-dimension 0 open stratum is open and dense. For notational purposes, reverse the conventions for indexing the stratifications in a stratified space, and index the open strata not by their dimension, but by their co-dimension. This is convenient since 
is infinite-dimensional if 
is not a finite set. By assumption, the open co-dimension 0 stratum of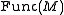 
is 
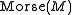, ie: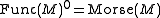 
. In a stratified space 
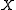, frequently 
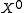is disconnected. The essential property of the co-dimension 1 stratum 
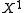is that any path in 
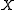which starts and ends in 
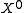can be approximated by a path that intersects 
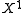transversely in finitely many points, and does not intersect 
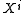for any 
.
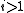Thus Cerf theory is the study of the positive co-dimensional strata of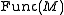
, i.e.: 
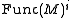for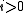 
. In the case of
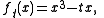
only for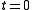
is the function not Morse, and
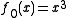
has a cubic degenerate critical point corresponding to the birth/death transition.
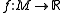is a Morse function, then near a critical point 
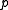it is conjugate to a function 
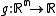of the form
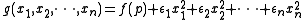
where
.
Cerf's 1-parameter theorem asserts the essential property of the co-dimension one stratum.
Precisely, if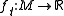
is a 1-parameter family of smooth functions on 
with 
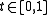, and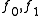 
Morse, then there exists a smooth 1-parameter family 
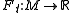such that 
, 
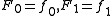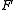is uniformly close to 
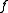in the 
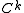-topology on functions 
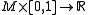. Moreover, 
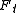is Morse at all but finitely many times. At a non-Morse time the function has only one degenerate critical point 
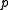, and near that point the family 
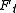is conjugate to the family
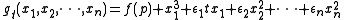
where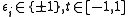
. If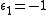 
this is a 1-parameter family of functions where two critical points are created (as 
increases), and for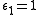 
it is a 1-parameter family of functions where two critical points are destroyed.
-Schoenflies problem for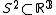
was solved by Alexander in 1924. His proof was adapted to the smooth case by Morse and Baiada. The essential property was used by Cerf in order to prove that every orientation-preserving diffeomorphism
of
is isotopic to the identity, seen as a 1-parameter extension of the Schoenflies theorem for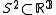
. The corollary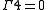 
at the time had wide implications in differential topology. The essential property was later used by Cerf to prove the pseudo-isotopy theorem
for high-dimensional simply-connected manifolds. The proof is a 1-parameter extension of Smale's proof of the h-cobordism theorem
(the rewriting of Smale's proof into the functional framework was done by Morse, also Milnor , and also by Cerf-Gramain-Morin following a suggestion of Thom).
Cerf's proof is built on the work of Thom and Mather . A useful modern summary of Thom and Mather's work from the period is the book of Golubitsky and Guillemin .
.
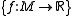was eventually developed by Sergeraert .
During the seventies, the classification problem for pseudo-isotopies of non-simply connected manifolds was solved by Hatcher
and Wagoner, discovering algebraic
-obstructions on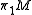
(
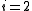) and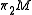 
(
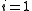) and by Igusa, discovering obstructions of a similar nature on 
(
) .
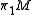Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, at the junction of singularity theory
Singularity theory
-The notion of singularity:In mathematics, singularity theory is the study of the failure of manifold structure. A loop of string can serve as an example of a one-dimensional manifold, if one neglects its width. What is meant by a singularity can be seen by dropping it on the floor...
and differential topology
Differential topology
In mathematics, differential topology is the field dealing with differentiable functions on differentiable manifolds. It is closely related to differential geometry and together they make up the geometric theory of differentiable manifolds.- Description :...
, Cerf theory is the study of families of smooth real-valued functions
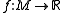
on a smooth manifold M, their generic singularities and the topology of the subspaces these singularities define, as subspaces of the function space.
An example
Marston MorseMarston Morse
Harold Calvin Marston Morse was an American mathematician best known for his work on the calculus of variations in the large, a subject where he introduced the technique of differential topology now known as Morse theory...
proved that, provided
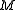is compact, any smooth function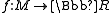could be approximated by a Morse function
Morse theory
In differential topology, the techniques of Morse theory give a very direct way of analyzing the topology of a manifold by studying differentiable functions on that manifold. According to the basic insights of Marston Morse, a differentiable function on a manifold will, in a typical case, reflect...
. So for many purposes, one can replace arbitrary functions on
by Morse functions.As a next step, one could ask, 'if you have a 1-parameter family of functions which start and end at Morse functions, can you assume the whole family is Morse?' In general the answer is no. Consider, for example, the family:
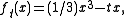
as a 1-parameter family of functions on
.At time
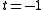
it has no critical points, but at time
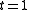
it is a Morse function with two critical points
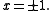
Jean Cerf showed that a 1-parameter family of functions between two Morse functions could be approximated by one that is Morse at all but finitely many degenerate times. The degeneracies involve a birth/death transition of critical points, as in the above example when
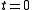an index 0 and index 1 critical point are created (as increases).A stratification of an infinite-dimensional space
Let's return to the general case that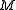 is a compact manifold.Let
denote the space of Morse functions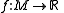and
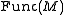the space of smooth functions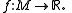Morse proved that
is an open and dense subset in the
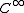topology.For the purposes of intuition, here is an analogy. Think of the Morse functions as the top-dimensional open stratum in a stratification
Topologically stratified space
In topology, a branch of mathematics, a topologically stratified space is a space X that has been decomposed into pieces called strata; these strata are topological manifolds and are required to fit together in a certain way...
of
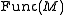(we make no claim that such a stratification exists, but suppose one does). Notice that in stratified spaces, the co-dimension 0 open stratum is open and dense. For notational purposes, reverse the conventions for indexing the stratifications in a stratified space, and index the open strata not by their dimension, but by their co-dimension. This is convenient since is infinite-dimensional if is not a finite set. 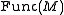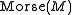By assumption, the open co-dimension 0 stratum of is , ie: 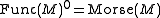. In a stratified space 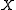, frequently 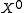is disconnected. The essential property of the co-dimension 1 stratum 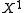is that any path in 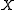which starts and ends in 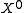can be approximated by a path that intersects 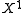transversely in finitely many points, and does not intersect 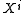for any 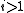.Thus Cerf theory is the study of the positive co-dimensional strata of
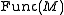, i.e.: 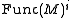for 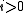. In the case of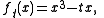only for
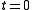is the function not Morse, and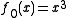has a cubic degenerate critical point corresponding to the birth/death transition.
A single time parameter, statement of theorem
The Morse Theorem asserts that if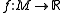 is a Morse function, then near a critical point 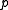it is conjugate to a function 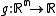of the form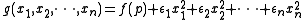where
.Cerf's 1-parameter theorem asserts the essential property of the co-dimension one stratum.
Precisely, if
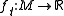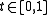is a 1-parameter family of smooth functions on with , and 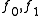Morse, then there exists a smooth 1-parameter family 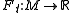such that 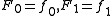, 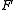is uniformly close to 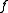in the 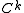-topology on functions 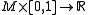. Moreover, 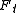is Morse at all but finitely many times. At a non-Morse time the function has only one degenerate critical point 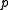, and near that point the family 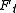is conjugate to the family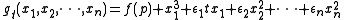where
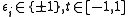. If 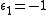this is a 1-parameter family of functions where two critical points are created (as increases), and for 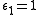it is a 1-parameter family of functions where two critical points are destroyed.Origins
The PLPiecewise linear manifold
In mathematics, a piecewise linear manifold is a topological manifold together with a piecewise linear structure on it. Such a structure can be defined by means of an atlas, such that one can pass from chart to chart in it by piecewise linear functions.An isomorphism of PL manifolds is called a PL...
-Schoenflies problem for
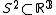was solved by Alexander in 1924. His proof was adapted to the smooth case by Morse and Baiada. The essential property was used by Cerf in order to prove that every orientation-preserving diffeomorphismDiffeomorphism
In mathematics, a diffeomorphism is an isomorphism in the category of smooth manifolds. It is an invertible function that maps one differentiable manifold to another, such that both the function and its inverse are smooth.- Definition :...
of
3-sphere
In mathematics, a 3-sphere is a higher-dimensional analogue of a sphere. It consists of the set of points equidistant from a fixed central point in 4-dimensional Euclidean space...
is isotopic to the identity, seen as a 1-parameter extension of the Schoenflies theorem for
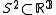. The corollary Exotic sphere
In differential topology, a mathematical discipline, an exotic sphere is a differentiable manifold M that is homeomorphic but not diffeomorphic to the standard Euclidean n-sphere...
at the time had wide implications in differential topology. The essential property was later used by Cerf to prove the pseudo-isotopy theorem
Pseudoisotopy theorem
In mathematics, the pseudoisotopy theorem is a theorem of Jean Cerf's which refers to the connectivity of a group of diffeomorphisms of a manifold.- Statement :...
for high-dimensional simply-connected manifolds. The proof is a 1-parameter extension of Smale's proof of the h-cobordism theorem
H-cobordism
A cobordism W between M and N is an h-cobordism if the inclusion mapsare homotopy equivalences...
(the rewriting of Smale's proof into the functional framework was done by Morse, also Milnor , and also by Cerf-Gramain-Morin following a suggestion of Thom).
Cerf's proof is built on the work of Thom and Mather . A useful modern summary of Thom and Mather's work from the period is the book of Golubitsky and Guillemin .
Applications
Beside the above mentioned applications, Robion Kirby used Cerf Theory as a key step in justifying the Kirby calculusKirby calculus
In mathematics, the Kirby calculus in geometric topology, named after Robion Kirby, is a method for modifying framed links in the 3-sphere using a finite set of moves, the Kirby moves...
.
Generalization
A stratification of the complement of an infinite co-dimension subspace of the space of smooth maps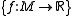 was eventually developed by Sergeraert .During the seventies, the classification problem for pseudo-isotopies of non-simply connected manifolds was solved by Hatcher
Allen Hatcher
Allen Edward Hatcher is an American topologist and also a noted author. His book Algebraic Topology, which is the first in a series, is considered by many to be one of the best introductions to the subject....
and Wagoner, discovering algebraic
K-theory
In mathematics, K-theory originated as the study of a ring generated by vector bundles over a topological space or scheme. In algebraic topology, it is an extraordinary cohomology theory known as topological K-theory. In algebra and algebraic geometry, it is referred to as algebraic K-theory. It...
-obstructions on
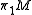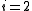() and 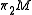(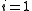) and by Igusa, discovering obstructions of a similar nature on () .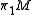