
Golden ratio base
Encyclopedia
Golden ratio base is a non-integer positional numeral system that uses the golden ratio
(the irrational number (1+√5)/2 ≈ 1.61803399... symbolized by the Greek letter
φ
) as its base. It is sometimes referred to as base-φ, golden mean base, phi-base, or, colloquially, phinary. Any non-negative real number can be represented as a base-φ numeral using only the digits 0 and 1, and avoiding the digit sequence "11" - this is called a standard form. A base-φ numeral that includes the digit sequence "11" can always be rewritten in standard form, using the algebraic properties of the base φ — most notably that φ+1 = φ2. For instance, 11φ = 100φ.
Despite using an irrational number
base, when using standard form, all non-negative integer
s have a unique representation as a terminating (finite) base-φ expansion. Other numbers have standard representations in base-φ, with rational number
s having recurring representations. These representations are unique, except that numbers with a terminating expansion also have a non-terminating expansion, as they do in base-10
; for example, 1=0.99999….
To "standardize" a numeral, we can use the following substitutions: 011φ = 100φ, 0200φ = 1001φ and 010φ = 101φ. We can apply the substitutions in any order we like, as the result is the same. Below, the substitutions used are on the right, the resulting number on the left.
211.01φ
300.01φ 011φ → 100φ
1101.01φ 0200φ → 1001φ
10001.01φ 011φ → 100φ (again)
10001.101φ 010φ → 101φ
10000.011φ 010φ → 101φ (again)
10000.1φ 011φ → 100φ (again)
Any positive number with a non-standard terminating base-φ representation can be uniquely standardized in this manner. If we get to a point where all digits are "0" or "1", except for the first digit being negative, then the number is negative. This can be converted to the negative of a base-φ representation by negating
every digit, standardizing the result, and then marking it as negative. For example, use a minus sign, or some other significance to denote negative numbers. If the arithmetic is being performed on a computer, an error message
may be returned.
Note that when adding the digits "9" and "1", the result is a single digit "(10)", "A" or similar, as we are not working in decimal.
1×1 = 1, φ × φ = 1 + φ and 1/φ = −1 + φ. Therefore, we can compute
and
So, using integer values only, we can add, subtract and multiply numbers of the form (a + bφ), and even represent positive and negative integer powers
of φ. (Note that φ−1 = 1/φ.)
(a + bφ) > (c + dφ) if and only if 2(a − c) − (d − b) > (d − b) × √5. If one side is negative, the other positive, the comparison is trivial. Otherwise, square both sides, to get an integer comparison, reversing the comparison direction if both sides were negative. On squaring both sides, the √5 is replaced with the integer 5.
So, using integer values only, we can also compare numbers of the form (a + bφ).
The above procedure will never result in the sequence "11", since 11φ = 100φ, so getting a "11" would mean we missed a "1" prior to the sequence "11".
Start, e. g., with integer=5, with the result so far being ...00000.00000...φ
Highest power of φ ≤ 5 is φ3 = 1 + 2φ ≈ 4.236067977
Subtracting this from 5, we have 5 - (1 + 2φ) = 4 − 2φ ≈ 0.763932023..., the result so far being 1000.00000...φ
Highest power of φ ≤ 4 − 2φ ≈ 0.763932023... is φ−1 = −1 + 1φ ≈ 0.618033989...
Subtracting this from 4 − 2φ ≈ 0.763932023..., we have 4 − 2φ − (−1 + 1φ) = 5 − 3φ ≈ 0.145898034..., the result so far being 1000.10000...φ
Highest power of φ ≤ 5 − 3φ ≈ 0.145898034... is φ−4 = 5 − 3φ ≈ 0.145898034...
Subtracting this from 5 − 3φ ≈ 0.145898034..., we have 5 − 3φ − (5 − 3φ) = 0 + 0φ = 0, with the final result being 1000.1001φ.
. In base-φ, the numeral 0.1010101... can be seen to be equal to 1 in several ways:
This non-uniqueness is a feature of the numeration system, since both 1.0000 and 0.101010... are in standard form.
In general, the final 1 of any number in base-φ can be replaced with a recurring 01 without changing the value of that number.
Q[√5] = Q + √5Q, the field generated by the rational number
s and √5. Conversely any recurring (or terminating) base-φ expansion is a non-negative element of Q[√5]. Some examples (with spaces added for emphasis):
The justification that a rational gives a recurring expansion is analogous to the equivalent proof for a base-n numeration system (n=2,3,4,...). Essentially in base-φ long division
there are only a finite number of possible remainders, and so once there must be a recurring pattern. For example with 1/2 = 1/10.01φ = 100φ/1001φ long division looks like this (note that base-φ subtraction may be hard to follow at first):
.0 1 0 0 1
________________________
1 0 0 1 ) 1 0 0.0 0 0 0 0 0 0 0
1 0 0 1 trade: 10000 = 1100 = 1011
------- so 10000-1001 = 1011-1001 = 10
1 0 0 0 0
1 0 0 1
-------
etc.
The converse is also true, in that a number with a recurring base-φ; representation is an element of the field Q[√5]. This follows from the observation that a recurring representation with period k involves a geometric series with ratio φ-k, which will sum to an element of Q[√5].
of two base-φ numbers, add each pair of digits, without carry, and then convert the numeral to standard form. For subtraction
, subtract each pair of digits without borrow (borrow is a negative amount of carry), and then convert the numeral to standard form. For multiplication
, multiply in the typical base-10 manner, without carry, then convert the numeral to standard form.
For example
The subtraction seen here uses a modified form of the standard "trading" algorithm for subtraction.
can be represented as a finite base-φ number. In other words, all finitely representable base-φ numbers are either integers or (more likely) an irrational in the field
Q[√5]. Due to long division having only a finite number of possible remainders, a division of two integers (or other numbers with finite base-φ representation) will have a recurring expansion, as demonstrated above.
is a closely related numeration system used for integers. In this system, only digits 0 and 1 are used and the place values of the digits are the Fibonacci number
s. As with base-φ, the digit sequence "11" is avoided by rearranging to a standard form, using the Fibonacci recurrence relation
Fk+1 = Fk + Fk-1. For example
Golden ratio
In mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989...
(the irrational number (1+√5)/2 ≈ 1.61803399... symbolized by the Greek letter
Greek alphabet
The Greek alphabet is the script that has been used to write the Greek language since at least 730 BC . The alphabet in its classical and modern form consists of 24 letters ordered in sequence from alpha to omega...
φ
Phi
Phi may refer to:In language:*Phi, the Greek letter Φ,φ, the symbol for voiceless bilabial fricativeIn mathematics:*The Golden ratio*Euler's totient function*A statistical measure of association reported with the chi-squared test...
) as its base. It is sometimes referred to as base-φ, golden mean base, phi-base, or, colloquially, phinary. Any non-negative real number can be represented as a base-φ numeral using only the digits 0 and 1, and avoiding the digit sequence "11" - this is called a standard form. A base-φ numeral that includes the digit sequence "11" can always be rewritten in standard form, using the algebraic properties of the base φ — most notably that φ+1 = φ2. For instance, 11φ = 100φ.
Despite using an irrational number
Irrational number
In mathematics, an irrational number is any real number that cannot be expressed as a ratio a/b, where a and b are integers, with b non-zero, and is therefore not a rational number....
base, when using standard form, all non-negative integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s have a unique representation as a terminating (finite) base-φ expansion. Other numbers have standard representations in base-φ, with rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s having recurring representations. These representations are unique, except that numbers with a terminating expansion also have a non-terminating expansion, as they do in base-10
Decimal
The decimal numeral system has ten as its base. It is the numerical base most widely used by modern civilizations....
; for example, 1=0.99999….
Examples
| Decimal | Powers of φ | Base φ |
|---|---|---|
| 1 | φ0 | 1 |
| 2 | φ1 + φ−2 | 10.01 |
| 3 | φ2 + φ−2 | 100.01 |
| 4 | φ2 + φ0 + φ−2 | 101.01 |
| 5 | φ3 + φ−1 + φ−4 | 1000.1001 |
| 6 | φ3 + φ1 + φ−4 | 1010.0001 |
| 7 | φ4 + φ−4 | 10000.0001 |
| 8 | φ4 + φ0 + φ−4 | 10001.0001 |
| 9 | φ4 + φ1 + φ−2 + φ−4 | 10010.0101 |
| 10 | φ4 + φ2 + φ−2 + φ−4 | 10100.0101 |
Writing golden ratio base numbers in standard form
211.01φ is not a standard base-φ numeral, since it contains a "11" and a "2", which isn't a "0" or "1", and contains a 1=-1, which isn't a "0" or "1" either.To "standardize" a numeral, we can use the following substitutions: 011φ = 100φ, 0200φ = 1001φ and 010φ = 101φ. We can apply the substitutions in any order we like, as the result is the same. Below, the substitutions used are on the right, the resulting number on the left.
211.01φ
300.01φ 011φ → 100φ
1101.01φ 0200φ → 1001φ
10001.01φ 011φ → 100φ (again)
10001.101φ 010φ → 101φ
10000.011φ 010φ → 101φ (again)
10000.1φ 011φ → 100φ (again)
Any positive number with a non-standard terminating base-φ representation can be uniquely standardized in this manner. If we get to a point where all digits are "0" or "1", except for the first digit being negative, then the number is negative. This can be converted to the negative of a base-φ representation by negating
Negation (algebra)
Negation is the mathematical operation that reverses the sign of a number. Thus the negation of a positive number is negative, and the negation of a negative number is positive. The negation of zero is zero...
every digit, standardizing the result, and then marking it as negative. For example, use a minus sign, or some other significance to denote negative numbers. If the arithmetic is being performed on a computer, an error message
Error message
An error message is information displayed when an unexpected condition occurs, usually on a computer or other device. On modern operating systems with graphical user interfaces, error messages are often displayed using dialog boxes...
may be returned.
Note that when adding the digits "9" and "1", the result is a single digit "(10)", "A" or similar, as we are not working in decimal.
Representing integers as golden ratio base numbers
We can either consider our integer to be the (only) digit of a nonstandard base-φ numeral, and standardize it, or do the following:1×1 = 1, φ × φ = 1 + φ and 1/φ = −1 + φ. Therefore, we can compute
- (a + bφ) + (c + dφ) = ((a + c) + (b + d)φ),
- (a + bφ) − (c + dφ) = ((a − c) + (b − d)φ)
and
- (a + bφ) × (c + dφ) = ((ac + bd) + (ad + bc + bd)φ).
So, using integer values only, we can add, subtract and multiply numbers of the form (a + bφ), and even represent positive and negative integer powers
Exponentiation
Exponentiation is a mathematical operation, written as an, involving two numbers, the base a and the exponent n...
of φ. (Note that φ−1 = 1/φ.)
(a + bφ) > (c + dφ) if and only if 2(a − c) − (d − b) > (d − b) × √5. If one side is negative, the other positive, the comparison is trivial. Otherwise, square both sides, to get an integer comparison, reversing the comparison direction if both sides were negative. On squaring both sides, the √5 is replaced with the integer 5.
So, using integer values only, we can also compare numbers of the form (a + bφ).
- To convert an integer x to a base-φ number, note that x = (x + 0φ).
- Subtract the highest power of φ, which is still smaller than the number we have, to get our new number, and record a "1" in the appropriate place in the resulting base-φ number.
- Unless our number is 0, go to step 2.
- Finished.
The above procedure will never result in the sequence "11", since 11φ = 100φ, so getting a "11" would mean we missed a "1" prior to the sequence "11".
Start, e. g., with integer=5, with the result so far being ...00000.00000...φ
Highest power of φ ≤ 5 is φ3 = 1 + 2φ ≈ 4.236067977
Subtracting this from 5, we have 5 - (1 + 2φ) = 4 − 2φ ≈ 0.763932023..., the result so far being 1000.00000...φ
Highest power of φ ≤ 4 − 2φ ≈ 0.763932023... is φ−1 = −1 + 1φ ≈ 0.618033989...
Subtracting this from 4 − 2φ ≈ 0.763932023..., we have 4 − 2φ − (−1 + 1φ) = 5 − 3φ ≈ 0.145898034..., the result so far being 1000.10000...φ
Highest power of φ ≤ 5 − 3φ ≈ 0.145898034... is φ−4 = 5 − 3φ ≈ 0.145898034...
Subtracting this from 5 − 3φ ≈ 0.145898034..., we have 5 − 3φ − (5 − 3φ) = 0 + 0φ = 0, with the final result being 1000.1001φ.
Non-uniqueness
Just as with any base-n system, numbers with a terminating representation have an alternative recurring representation. In base-10, this relies on the observation that 0.999...=10.999...
In mathematics, the repeating decimal 0.999... denotes a real number that can be shown to be the number one. In other words, the symbols 0.999... and 1 represent the same number...
. In base-φ, the numeral 0.1010101... can be seen to be equal to 1 in several ways:
- Conversion to nonstandard form: 1 = 0.11φ = 0.1011φ = 0.101011φ = ... = 0.10101010....φ
- Geometric series: 1.0101010...φ is equal to
-
-
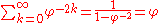
- Difference between "shifts": φ2 x - x = 10.101010...φ - 0.101010...φ = 10φ = φ so that x = φ/(φ2 − 1) = 1
-
This non-uniqueness is a feature of the numeration system, since both 1.0000 and 0.101010... are in standard form.
In general, the final 1 of any number in base-φ can be replaced with a recurring 01 without changing the value of that number.
Representing rational numbers as golden ratio base numbers
Every non-negative rational number can be represented as a recurring base-φ expansion, as can any non-negative element of the fieldField (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
Q[√5] = Q + √5Q, the field generated by the rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s and √5. Conversely any recurring (or terminating) base-φ expansion is a non-negative element of Q[√5]. Some examples (with spaces added for emphasis):
- 1/2 ≈ 0.010 010 010 010 ... φ
- 1/3 ≈ 0.00101000 00101000 00101000... φ
- √5 = 10.1φ
- 2+(1/13)√5 ≈ 10.010 1000100010101000100010000000 1000100010101000100010000000 1000100010101000100010000000 ...φ
The justification that a rational gives a recurring expansion is analogous to the equivalent proof for a base-n numeration system (n=2,3,4,...). Essentially in base-φ long division
Long division
In arithmetic, long division is a standard procedure suitable for dividing simple or complex multidigit numbers. It breaks down a division problem into a series of easier steps. As in all division problems, one number, called the dividend, is divided by another, called the divisor, producing a...
there are only a finite number of possible remainders, and so once there must be a recurring pattern. For example with 1/2 = 1/10.01φ = 100φ/1001φ long division looks like this (note that base-φ subtraction may be hard to follow at first):
.0 1 0 0 1
________________________
1 0 0 1 ) 1 0 0.0 0 0 0 0 0 0 0
1 0 0 1 trade: 10000 = 1100 = 1011
------- so 10000-1001 = 1011-1001 = 10
1 0 0 0 0
1 0 0 1
-------
etc.
The converse is also true, in that a number with a recurring base-φ; representation is an element of the field Q[√5]. This follows from the observation that a recurring representation with period k involves a geometric series with ratio φ-k, which will sum to an element of Q[√5].
Representing irrational numbers of note as golden ratio base numbers
The base-φ representations of some interesting numbers:- πPi' is a mathematical constant that is the ratio of any circle's circumference to its diameter. is approximately equal to 3.14. Many formulae in mathematics, science, and engineering involve , which makes it one of the most important mathematical constants...
≈ 100.0100 1010 1001 0001 0101 0100 0001 0100 ...φ - eE (mathematical constant)The mathematical constant ' is the unique real number such that the value of the derivative of the function at the point is equal to 1. The function so defined is called the exponential function, and its inverse is the natural logarithm, or logarithm to base...
≈ 100.0000 1000 0100 1000 0000 0100 ...φ - √2Square root of 2The square root of 2, often known as root 2, is the positive algebraic number that, when multiplied by itself, gives the number 2. It is more precisely called the principal square root of 2, to distinguish it from the negative number with the same property.Geometrically the square root of 2 is the...
≈ 1.0100 0001 0100 1010 0100 0000 0101 0000 0000 0101 ...φ - φGolden ratioIn mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989...
= (1+√5)/2 = 10φ - √5 = 10.1φ
Addition, subtraction, and multiplication
It is possible to adapt all the standard algorithms of base-10 arithmetic to base-φ arithmetic. There are two approaches to this:Calculate, then convert to standard form
For additionAddition
Addition is a mathematical operation that represents combining collections of objects together into a larger collection. It is signified by the plus sign . For example, in the picture on the right, there are 3 + 2 apples—meaning three apples and two other apples—which is the same as five apples....
of two base-φ numbers, add each pair of digits, without carry, and then convert the numeral to standard form. For subtraction
Subtraction
In arithmetic, subtraction is one of the four basic binary operations; it is the inverse of addition, meaning that if we start with any number and add any number and then subtract the same number we added, we return to the number we started with...
, subtract each pair of digits without borrow (borrow is a negative amount of carry), and then convert the numeral to standard form. For multiplication
Multiplication
Multiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....
, multiply in the typical base-10 manner, without carry, then convert the numeral to standard form.
For example
- 2+3 = 10.01 + 100.01 = 110.02 = 110.1001 = 1000.1001
- 2×3 = 10.01 × 100.01 = 1000.1 + 1.0001 = 1001.1001 = 1010.0001
- 7-2 = 10000.0001 - 10.01 = 10010.0101 = 1110.0101 = 1001.0101 = 1000.1001
Avoid digits other than 0 and 1
A more "native" approach is to avoid having to add digits 1+1 or to subtract 0-1. This is done by reorganising the operands into nonstandard form so that these combinations do not occur. For example- 2+3 = 10.01 + 100.01 = 10.01 + 100.0011 = 110.0111 = 1000.1001
- 7-2 = 10000.0001 - 10.01 = 1100.0001 - 10.01 = 1011.0001 - 10.01 = 1010.1101 - 10.01 = 1000.1001
The subtraction seen here uses a modified form of the standard "trading" algorithm for subtraction.
Division
No non-integer rational numberRational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
can be represented as a finite base-φ number. In other words, all finitely representable base-φ numbers are either integers or (more likely) an irrational in the field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
Q[√5]. Due to long division having only a finite number of possible remainders, a division of two integers (or other numbers with finite base-φ representation) will have a recurring expansion, as demonstrated above.
Relationship with Fibonacci coding
Fibonacci codingFibonacci coding
In mathematics, Fibonacci coding is a universal code which encodes positive integers into binary code words. Each code word ends with "11" and contains no other instances of "11" before the end.-Definition:...
is a closely related numeration system used for integers. In this system, only digits 0 and 1 are used and the place values of the digits are the Fibonacci number
Fibonacci number
In mathematics, the Fibonacci numbers are the numbers in the following integer sequence:0,\;1,\;1,\;2,\;3,\;5,\;8,\;13,\;21,\;34,\;55,\;89,\;144,\; \ldots\; ....
s. As with base-φ, the digit sequence "11" is avoided by rearranging to a standard form, using the Fibonacci recurrence relation
Recurrence relation
In mathematics, a recurrence relation is an equation that recursively defines a sequence, once one or more initial terms are given: each further term of the sequence is defined as a function of the preceding terms....
Fk+1 = Fk + Fk-1. For example
-
- 30 = 1×21 + 0×13 + 1×8 + 0×5 + 0×3 + 0×2 + 1×1 + 0×1 = 10100010fib.

