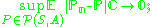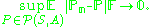Glivenko-Cantelli theorem
Encyclopedia
In the theory of probability, the Glivenko–Cantelli theorem, named after Valery Ivanovich Glivenko
and Francesco Paolo Cantelli
, determines the asymptotic behaviour of the empirical distribution function
as the number of independent and identically distributed
observations grows. This uniform convergence of more general empirical measure
s becomes an important property of the Glivenko–Cantelli classes of functions or sets. The Glivenko–Cantelli classes arise in Vapnik–Chervonenkis theory, with applications to machine learning
. Applications can be found in econometrics
making use of M-estimator
s
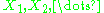 are independent and identically-distributed random variables in
are independent and identically-distributed random variables in  with common cumulative distribution function
with common cumulative distribution function
F(x). The empirical distribution function
for is defined by
is defined by

where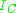 is the indicator function of the set
is the indicator function of the set 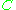 . For every (fixed) x,
. For every (fixed) x, 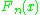 is a sequence of random variables which converge to F(x) almost surely
is a sequence of random variables which converge to F(x) almost surely
by the strong law of large numbers
, that is,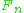 converges to F pointwise
converges to F pointwise
. Glivenko and Cantelli strengthened this result by proving uniform convergence of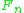 to F.
to F.
Theorem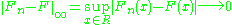 almost surely.
almost surely.
This theorem originates with Valery Glivenko
, and Francesco Cantelli
, in 1933.
Remarks
 by an arbitrary set C from a class of sets
by an arbitrary set C from a class of sets  to obtain an empirical measure
to obtain an empirical measure
indexed by sets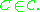
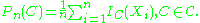
Further generalization is the map induced by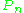 on measurable real-valued functions f, which is given by
on measurable real-valued functions f, which is given by
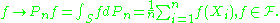
Then it becomes an important property of these classes that the strong law of large numbers
holds uniformly on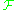 or
or  .
.
 with a sigma algebra of Borel subsets
with a sigma algebra of Borel subsets
A and a probability measure
P. For a class of subsets,

and a class of functions
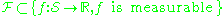
define random variables


where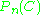 is the empirical measure,
is the empirical measure, 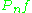 is the corresponding map, and
is the corresponding map, and
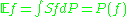 , assuming that it exists.
, assuming that it exists.
Definitions
Theorem (Vapnik and Chervonenkis, 1968)
Valery Ivanovich Glivenko
Valery Ivanovich Glivenko / January 2, 1897 in Kiev, died February 15, 1940 in Moscow) was a Soviet mathematician. He worked in foundations of mathematics and probability theory. He taught at Liebknecht University until his death at age 43....
and Francesco Paolo Cantelli
Francesco Paolo Cantelli
Francesco Paolo Cantelli was an Italian mathematician. He was the founder of the Istituto Italiano degli Attuari for the applications of mathematics and probability to economics....
, determines the asymptotic behaviour of the empirical distribution function
Empirical distribution function
In statistics, the empirical distribution function, or empirical cdf, is the cumulative distribution function associated with the empirical measure of the sample. This cdf is a step function that jumps up by 1/n at each of the n data points. The empirical distribution function estimates the true...
as the number of independent and identically distributed
Independent and identically distributed random variables
In probability theory and statistics, a sequence or other collection of random variables is independent and identically distributed if each random variable has the same probability distribution as the others and all are mutually independent....
observations grows. This uniform convergence of more general empirical measure
Empirical measure
In probability theory, an empirical measure is a random measure arising from a particular realization of a sequence of random variables. The precise definition is found below. Empirical measures are relevant to mathematical statistics....
s becomes an important property of the Glivenko–Cantelli classes of functions or sets. The Glivenko–Cantelli classes arise in Vapnik–Chervonenkis theory, with applications to machine learning
Machine learning
Machine learning, a branch of artificial intelligence, is a scientific discipline concerned with the design and development of algorithms that allow computers to evolve behaviors based on empirical data, such as from sensor data or databases...
. Applications can be found in econometrics
Econometrics
Econometrics has been defined as "the application of mathematics and statistical methods to economic data" and described as the branch of economics "that aims to give empirical content to economic relations." More precisely, it is "the quantitative analysis of actual economic phenomena based on...
making use of M-estimator
M-estimator
In statistics, M-estimators are a broad class of estimators, which are obtained as the minima of sums of functions of the data. Least-squares estimators and many maximum-likelihood estimators are M-estimators. The definition of M-estimators was motivated by robust statistics, which contributed new...
s
Glivenko–Cantelli theorem
Assume that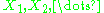 are independent and identically-distributed random variables in
are independent and identically-distributed random variables in  with common cumulative distribution function
with common cumulative distribution functionCumulative distribution function
In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
F(x). The empirical distribution function
Empirical distribution function
In statistics, the empirical distribution function, or empirical cdf, is the cumulative distribution function associated with the empirical measure of the sample. This cdf is a step function that jumps up by 1/n at each of the n data points. The empirical distribution function estimates the true...
for
 is defined by
is defined by
where
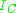 is the indicator function of the set
is the indicator function of the set 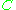 . For every (fixed) x,
. For every (fixed) x, 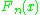 is a sequence of random variables which converge to F(x) almost surely
is a sequence of random variables which converge to F(x) almost surelyAlmost surely
In probability theory, one says that an event happens almost surely if it happens with probability one. The concept is analogous to the concept of "almost everywhere" in measure theory...
by the strong law of large numbers
Law of large numbers
In probability theory, the law of large numbers is a theorem that describes the result of performing the same experiment a large number of times...
, that is,
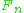 converges to F pointwise
converges to F pointwisePointwise convergence
In mathematics, pointwise convergence is one of various senses in which a sequence of functions can converge to a particular function.-Definition:...
. Glivenko and Cantelli strengthened this result by proving uniform convergence of
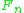 to F.
to F.Theorem
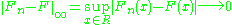 almost surely.
almost surely.This theorem originates with Valery Glivenko
Valery Ivanovich Glivenko
Valery Ivanovich Glivenko / January 2, 1897 in Kiev, died February 15, 1940 in Moscow) was a Soviet mathematician. He worked in foundations of mathematics and probability theory. He taught at Liebknecht University until his death at age 43....
, and Francesco Cantelli
Francesco Paolo Cantelli
Francesco Paolo Cantelli was an Italian mathematician. He was the founder of the Istituto Italiano degli Attuari for the applications of mathematics and probability to economics....
, in 1933.
Remarks
- If
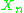 is a stationary ergodic sequence, then
is a stationary ergodic sequence, then 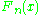 converges almost surely to
converges almost surely to 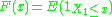 . The Glivenko–Cantelli theorem gives a stronger mode of convergence than this in the iid case.
. The Glivenko–Cantelli theorem gives a stronger mode of convergence than this in the iid case. - An even stronger uniform convergence result for the empirical distribution function is available in the form of an extended type of law of the iterated logarithmLaw of the iterated logarithmIn probability theory, the law of the iterated logarithm describes the magnitude of the fluctuations of a random walk. The original statement of the law of the iterated logarithm is due to A. Y. Khinchin . Another statement was given by A.N...
. See asymptotic properties of the Empirical distribution function for this and related results.
Empirical measures
One can generalize the empirical distribution function by replacing the set by an arbitrary set C from a class of sets
by an arbitrary set C from a class of sets  to obtain an empirical measure
to obtain an empirical measureEmpirical measure
In probability theory, an empirical measure is a random measure arising from a particular realization of a sequence of random variables. The precise definition is found below. Empirical measures are relevant to mathematical statistics....
indexed by sets
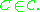
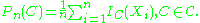
Further generalization is the map induced by
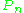 on measurable real-valued functions f, which is given by
on measurable real-valued functions f, which is given by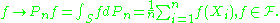
Then it becomes an important property of these classes that the strong law of large numbers
Law of large numbers
In probability theory, the law of large numbers is a theorem that describes the result of performing the same experiment a large number of times...
holds uniformly on
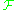 or
or  .
.Glivenko–Cantelli class
Consider a set with a sigma algebra of Borel subsets
with a sigma algebra of Borel subsetsBorel set
In mathematics, a Borel set is any set in a topological space that can be formed from open sets through the operations of countable union, countable intersection, and relative complement...
A and a probability measure
Probability measure
In mathematics, a probability measure is a real-valued function defined on a set of events in a probability space that satisfies measure properties such as countable additivity...
P. For a class of subsets,

and a class of functions
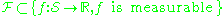
define random variables


where
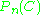 is the empirical measure,
is the empirical measure, 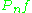 is the corresponding map, and
is the corresponding map, and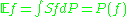 , assuming that it exists.
, assuming that it exists.Definitions
- A class
 is called a Glivenko–Cantelli class (or GC class) with respect to a probability measure P if any of the following equivalent statements is true.
is called a Glivenko–Cantelli class (or GC class) with respect to a probability measure P if any of the following equivalent statements is true.
-
- 1.
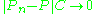 almost surely as
almost surely as  .
. - 2.
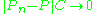 in probability as
in probability as  .
. - 3.
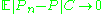 , as
, as 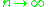 (convergence in mean).
(convergence in mean).
- 1.
- The Glivenko–Cantelli classes of functions are defined similarly.
- A class is called a universal Glivenko–Cantelli class if it is a GC class with respect to any probability measure P on (S,A).
- A class is called uniformly Glivenko–Cantelli if the convergence occurs uniformly over all probability measures P on (S,A):
Theorem (Vapnik and Chervonenkis, 1968)
- A class of sets
 is uniformly GC if and only if it is a Vapnik–Chervonenkis class.
is uniformly GC if and only if it is a Vapnik–Chervonenkis class.
Examples
- Let
 and
and 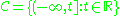 . The classical Glivenko–Cantelli theorem implies that this class is a universal GC class. Furthermore, by Kolmogorov's theoremKolmogorov-Smirnov testIn statistics, the Kolmogorov–Smirnov test is a nonparametric test for the equality of continuous, one-dimensional probability distributions that can be used to compare a sample with a reference probability distribution , or to compare two samples...
. The classical Glivenko–Cantelli theorem implies that this class is a universal GC class. Furthermore, by Kolmogorov's theoremKolmogorov-Smirnov testIn statistics, the Kolmogorov–Smirnov test is a nonparametric test for the equality of continuous, one-dimensional probability distributions that can be used to compare a sample with a reference probability distribution , or to compare two samples...
,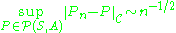 , that is
, that is  is uniformly Glivenko–Cantelli class.
is uniformly Glivenko–Cantelli class.
- Let P be a nonatomicAtom (measure theory)In mathematics, more precisely in measure theory, an atom is a measurable set which has positive measure and contains no set of smaller but positive measure...
probability measure on S and be a class of all finite subsets in S. Because
be a class of all finite subsets in S. Because  ,
, 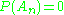 ,
, 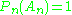 , we have that
, we have that  and so
and so  is not a GC class with respect to P.
is not a GC class with respect to P.
See also
- Donsker's theoremDonsker's theoremIn probability theory, Donsker's theorem, named after M. D. Donsker, identifies a certain stochastic process as a limit of empirical processes. It is sometimes called the functional central limit theorem....
- Dvoretzky–Kiefer–Wolfowitz inequalityDvoretzky–Kiefer–Wolfowitz inequalityIn the theory of probability and statistics, the Dvoretzky–Kiefer–Wolfowitz inequality predicts how close an empirically determined distribution function will be to the distribution function from which the empirical samples are drawn...
– strengthens Glivenko–Cantelli theorem by quantifying the rate of convergence.
Further reading
- Dudley, R. M.Richard M. DudleyRichard Mansfield Dudley is Professor of Mathematics at the Massachusetts Institute of Technology. He received his PhD at Princeton University in 1962 under the supervision of Edward Nelson and Gilbert Hunt. He was a Putnam Fellow in 1958....
(1999). Uniform Central Limit Theorems, Cambridge University Press. ISBN 0 521 46102 2. - Shorack, G.R., Wellner J.A. (1986) Empirical Processes with Applications to Statistics, Wiley. ISBN 0-471-86725-X.
- van der Vaart, A.W. and Wellner, J.A. (1996) Weak Convergence and Empirical Processes, Springer. ISBN 0-387-94640-3.