In statistics

Statistics

Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....

, the empirical distribution function, or empirical cdf, is the cumulative distribution function

Cumulative distribution function

In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...

 associated with the empirical measure

Empirical measure

In probability theory, an empirical measure is a random measure arising from a particular realization of a sequence of random variables. The precise definition is found below. Empirical measures are relevant to mathematical statistics....

 of the sample

Sample (statistics)

In statistics, a sample is a subset of a population. Typically, the population is very large, making a census or a complete enumeration of all the values in the population impractical or impossible. The sample represents a subset of manageable size...

. This cdf is a step function

Step function

In mathematics, a function on the real numbers is called a step function if it can be written as a finite linear combination of indicator functions of intervals...

 that jumps up by 1/n at each of the n data points. The empirical distribution function estimates the true underlying cdf of the points in the sample. A number of results exist which allow to quantify the rate of convergence of the empirical cdf to its limit.

Definition

Let (x₁, …, x_n) be iid real random variables with the common cdf

Cumulative distribution function

In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...

 F(t). Then the empirical distribution function is defined as

where 1{A} is the indicator of event

Event (probability theory)

In probability theory, an event is a set of outcomes to which a probability is assigned. Typically, when the sample space is finite, any subset of the sample space is an event...

 A. For a fixed t, the indicator 1{x_i ≤ t} is a Bernoulli random variable with parameter , hence $\backslash scriptstyle\; n\; \backslash hat\; F\_n(t)$ is a binomial random variable with mean

Mean

In statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....

 nF(t) and variance

Variance

In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...

 . This implies that $\backslash scriptstyle\; \backslash hat\; F\_n(t)$ is an unbiased

Bias of an estimator

In statistics, bias of an estimator is the difference between this estimator's expected value and the true value of the parameter being estimated. An estimator or decision rule with zero bias is called unbiased. Otherwise the estimator is said to be biased.In ordinary English, the term bias is...

 estimator for F(t).

Asymptotic properties

By the strong law of large numbers, the estimator $\backslash scriptstyle\backslash hat\{F\}\_n(t)$ converges to F(t) as almost surely, for every value of t:

thus the estimator $\backslash scriptstyle\backslash hat\{F\}\_n(t)$ is consistent

Consistent estimator

In statistics, a sequence of estimators for parameter θ0 is said to be consistent if this sequence converges in probability to θ0...

. This expression asserts the pointwise convergence of the empirical distribution function to the true cdf. There is a stronger result, called the Glivenko–Cantelli theorem, which states that the convergence in fact happens uniformly over t:

The sup-norm in this expression is called the Kolmogorov–Smirnov statistic for testing the goodness-of-fit between the empirical distribution $\backslash scriptstyle\backslash hat\{F\}\_n(t)$ and the assumed true cdf F. Other norm function

Norm (mathematics)

In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...

s may be reasonably used here instead of the sup-norm. For example, the L²-norm gives rise to the Cramér–von Mises statistic.

The asymptotic distribution can be further characterized in several different ways. First, the central limit theorem

Central limit theorem

In probability theory, the central limit theorem states conditions under which the mean of a sufficiently large number of independent random variables, each with finite mean and variance, will be approximately normally distributed. The central limit theorem has a number of variants. In its common...

 states that pointwise, $\backslash scriptstyle\backslash hat\{F\}\_n(t)$ has asymptotically normal distribution with the standard √n rate of convergence:

This result is extended by the Donsker’s theorem, which asserts that the empirical process

Empirical process

The study of empirical processes is a branch of mathematical statistics and a sub-area of probability theory. It is a generalization of the central limit theorem for empirical measures...

$\backslash scriptstyle\backslash sqrt\{n\}(\backslash hat\{F\}\_n\; -\; F)$, viewed as a function indexed by , converges in distribution in the Skorokhod space  to the mean-zero Gaussian process

Gaussian process

In probability theory and statistics, a Gaussian process is a stochastic process whose realisations consist of random values associated with every point in a range of times such that each such random variable has a normal distribution...

 , where B is the standard Brownian bridge

Brownian bridge

A Brownian bridge is a continuous-time stochastic process B whose probability distribution is the conditional probability distribution of a Wiener process W given the condition that B = B = 0.The expected value of the bridge is zero, with variance t, implying that the most...

. The covariance structure of this Gaussian process is

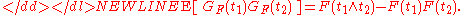
The uniform rate of convergence in Donsker’s theorem can be quantified by the result, known as the Hungarian embedding:

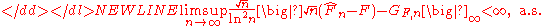
Alternatively, the rate of convergence of $\backslash scriptstyle\backslash sqrt\{n\}(\backslash hat\{F\}\_n-F)$ can also be quantified in terms of the asymptotic behavior of the sup-norm of this expression. Number of results exist in this venue, for example the Dvoretzky–Kiefer–Wolfowitz inequality

Dvoretzky–Kiefer–Wolfowitz inequality

In the theory of probability and statistics, the Dvoretzky–Kiefer–Wolfowitz inequality predicts how close an empirically determined distribution function will be to the distribution function from which the empirical samples are drawn...

 provides bound on the tail probabilities of $\backslash scriptstyle\backslash sqrt\{n\}\backslash |\backslash hat\{F\}\_n-F\backslash |\_\backslash infty$:

In fact, Kolmogorov has shown that if the cdf F is continuous, then the expression $\backslash scriptstyle\backslash sqrt\{n\}\backslash |\backslash hat\{F\}\_n-F\backslash |\_\backslash infty$ converges in distribution to ||B||_∞, which has the Kolmogorov distribution that does not depend on the form of F.

Another result, which follows from the law of the iterated logarithm

Law of the iterated logarithm

In probability theory, the law of the iterated logarithm describes the magnitude of the fluctuations of a random walk. The original statement of the law of the iterated logarithm is due to A. Y. Khinchin . Another statement was given by A.N...

, is that

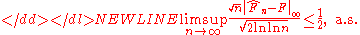
and

See also

• Càdlàg
  Càdlàg
  In mathematics, a càdlàg , RCLL , or corlol function is a function defined on the real numbers that is everywhere right-continuous and has left limits everywhere...
  
   functions
• Empirical probability
  Empirical probability
  Empirical probability, also known as relative frequency, or experimental probability, is the ratio of the number of "favorable" outcomes to the total number of trials, not in a sample space but in an actual sequence of experiments...
  
  
• Empirical process
  Empirical process
  The study of empirical processes is a branch of mathematical statistics and a sub-area of probability theory. It is a generalization of the central limit theorem for empirical measures...
  
  
• Kaplan Meier for censored processes
• Strassen’s theorem
• Survival function
  Survival function
  The survival function, also known as a survivor function or reliability function, is a property of any random variable that maps a set of events, usually associated with mortality or failure of some system, onto time. It captures the probability that the system will survive beyond a specified time...
  
  
• Dvoretzky–Kiefer–Wolfowitz inequality
  Dvoretzky–Kiefer–Wolfowitz inequality
  In the theory of probability and statistics, the Dvoretzky–Kiefer–Wolfowitz inequality predicts how close an empirically determined distribution function will be to the distribution function from which the empirical samples are drawn...
  
  

The source of this article is wikipedia, the free encyclopedia.  The text of this article is licensed under the GFDL.