Law of the iterated logarithm - AbsoluteAstronomy.com

Probability theory

Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...

, the law of the iterated logarithm describes the magnitude of the fluctuations of a random walk

Random walk

A random walk, sometimes denoted RW, is a mathematical formalisation of a trajectory that consists of taking successive random steps. For example, the path traced by a molecule as it travels in a liquid or a gas, the search path of a foraging animal, the price of a fluctuating stock and the...

. The original statement of the law of the iterated logarithm is due to A. Y. Khinchin (1924). Another statement was given by A.N. Kolmogorov

Andrey Kolmogorov

Andrey Nikolaevich Kolmogorov was a Soviet mathematician, preeminent in the 20th century, who advanced various scientific fields, among them probability theory, topology, intuitionistic logic, turbulence, classical mechanics and computational complexity.-Early life:Kolmogorov was born at Tambov...

in 1929.

Statement

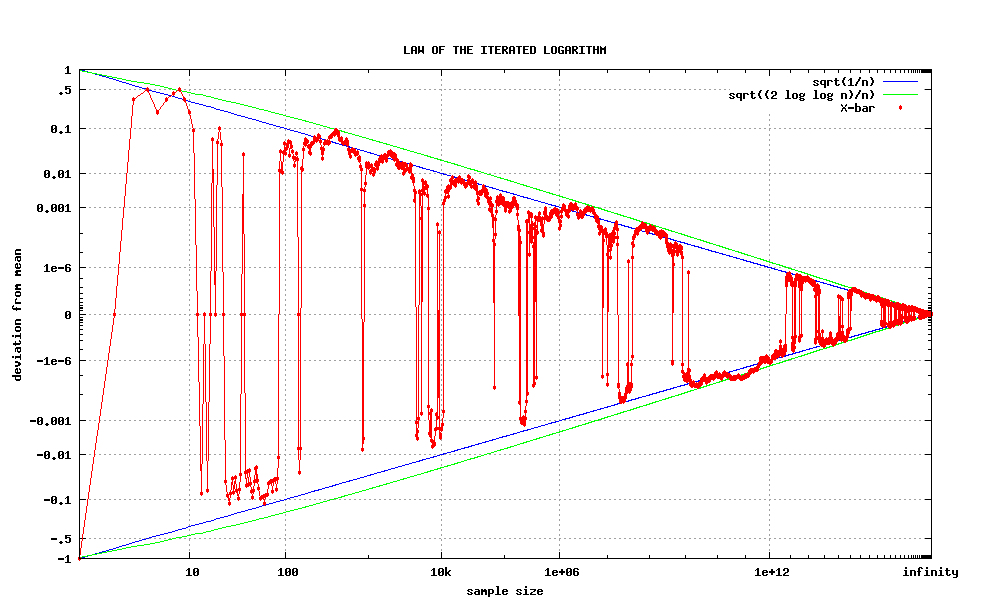
Let {Y_n} be independent, identically distributed random variables with means zero and unit variances. Let S_n = Y₁ + … + Y_n. Then

where “log” is the natural logarithm

Natural logarithm

The natural logarithm is the logarithm to the base e, where e is an irrational and transcendental constant approximately equal to 2.718281828...

, “lim sup” denotes the limit superior, and “a.s.” stands for “almost surely

Almost surely

In probability theory, one says that an event happens almost surely if it happens with probability one. The concept is analogous to the concept of "almost everywhere" in measure theory...

”.

Discussion

The law of iterated logarithms operates “in between” the law of large numbers

Law of large numbers

In probability theory, the law of large numbers is a theorem that describes the result of performing the same experiment a large number of times...

and the central limit theorem

Central limit theorem

In probability theory, the central limit theorem states conditions under which the mean of a sufficiently large number of independent random variables, each with finite mean and variance, will be approximately normally distributed. The central limit theorem has a number of variants. In its common...

. There are two versions of the law of large numbers — the weak and the strong — and they both claim that the sums S_n, scaled by n⁻¹, converge to zero, respectively in probability and almost surely:

On the other hand, the central limit theorem states that the sums S_n scaled by the factor n^−½ converge in distribution to a standard normal distribution, which implies that these quantities do not converge to anything neither in probability nor almost surely:

The law of the iterated logarithm provides the scaling factor where the two limits become different:

Thus, although the quantity

is less than any predefined ε > 0 with probability approaching one, that quantity will nevertheless be dropping out of that interval infinitely often, and in fact will be visiting the neighborhoods of any point in the interval (0,√2) almost surely.

Statement

Discussion

See also