
Ergodic sequence
Encyclopedia
In mathematics
, an ergodic sequence is a certain type of integer sequence
, having certain equidistribution properties.
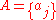 be an infinite, strictly increasing sequence
be an infinite, strictly increasing sequence
of positive integers. Then, given an integer q, this sequence is said to be ergodic mod q if, for all integers , one has
, one has
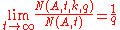
where
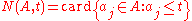
and card is the count (the number of elements) of a set, so that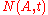 is the number of elements in the sequence A that are less than or equal to t, and
is the number of elements in the sequence A that are less than or equal to t, and

so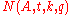 is the number of elements in the sequence A, less than t, that are equivalent to k modulo q. That is, a sequence is an ergodic sequence if it becomes uniformly distributed mod q as the sequence is taken to infinity.
is the number of elements in the sequence A, less than t, that are equivalent to k modulo q. That is, a sequence is an ergodic sequence if it becomes uniformly distributed mod q as the sequence is taken to infinity.
An equivalent definition is that the sum
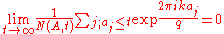
vanish for every integer k with .
.
If a sequence is ergodic for all q, then it is sometimes said to be ergodic for periodic systems.
Almost all
Bernoulli sequences, that is, sequences associated with a Bernoulli process
, are ergodic for all q. That is, let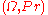 be a probability space
be a probability space
of random variable
s over two letters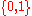 . Then, given
. Then, given 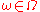 , the random variable
, the random variable 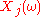 is 1 with some probability p and is zero with some probability 1-p; this is the definition of a Bernoulli process. Associated with each
is 1 with some probability p and is zero with some probability 1-p; this is the definition of a Bernoulli process. Associated with each  is the sequence of integers
is the sequence of integers
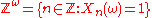
Then almost every sequence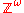 is ergodic.
is ergodic.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, an ergodic sequence is a certain type of integer sequence
Integer sequence
In mathematics, an integer sequence is a sequence of integers.An integer sequence may be specified explicitly by giving a formula for its nth term, or implicitly by giving a relationship between its terms...
, having certain equidistribution properties.
Definition
Let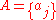 be an infinite, strictly increasing sequence
be an infinite, strictly increasing sequenceSequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
of positive integers. Then, given an integer q, this sequence is said to be ergodic mod q if, for all integers
 , one has
, one has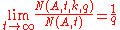
where
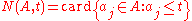
and card is the count (the number of elements) of a set, so that
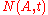 is the number of elements in the sequence A that are less than or equal to t, and
is the number of elements in the sequence A that are less than or equal to t, and
so
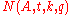 is the number of elements in the sequence A, less than t, that are equivalent to k modulo q. That is, a sequence is an ergodic sequence if it becomes uniformly distributed mod q as the sequence is taken to infinity.
is the number of elements in the sequence A, less than t, that are equivalent to k modulo q. That is, a sequence is an ergodic sequence if it becomes uniformly distributed mod q as the sequence is taken to infinity.An equivalent definition is that the sum
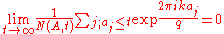
vanish for every integer k with
 .
.If a sequence is ergodic for all q, then it is sometimes said to be ergodic for periodic systems.
Examples
The sequence of positive integers is ergodic for all q.Almost all
Almost all
In mathematics, the phrase "almost all" has a number of specialised uses."Almost all" is sometimes used synonymously with "all but finitely many" or "all but a countable set" ; see almost....
Bernoulli sequences, that is, sequences associated with a Bernoulli process
Bernoulli process
In probability and statistics, a Bernoulli process is a finite or infinite sequence of binary random variables, so it is a discrete-time stochastic process that takes only two values, canonically 0 and 1. The component Bernoulli variables Xi are identical and independent...
, are ergodic for all q. That is, let
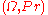 be a probability space
be a probability spaceProbability space
In probability theory, a probability space or a probability triple is a mathematical construct that models a real-world process consisting of states that occur randomly. A probability space is constructed with a specific kind of situation or experiment in mind...
of random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s over two letters
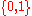 . Then, given
. Then, given 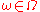 , the random variable
, the random variable 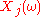 is 1 with some probability p and is zero with some probability 1-p; this is the definition of a Bernoulli process. Associated with each
is 1 with some probability p and is zero with some probability 1-p; this is the definition of a Bernoulli process. Associated with each  is the sequence of integers
is the sequence of integers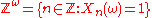
Then almost every sequence
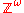 is ergodic.
is ergodic.See also
- Ergodic theoryErgodic theoryErgodic theory is a branch of mathematics that studies dynamical systems with an invariant measure and related problems. Its initial development was motivated by problems of statistical physics....
- Ergodic processErgodic processIn signal processing, a stochastic process is said to be ergodic if its statistical properties can be deduced from a single, sufficiently long sample of the process.- Specific definitions :...
, for the use of the term in signal processingSignal processingSignal processing is an area of systems engineering, electrical engineering and applied mathematics that deals with operations on or analysis of signals, in either discrete or continuous time...

