Minimax eversion
Encyclopedia
In geometry
, minimax eversions are a class of sphere eversions, constructed by using half-way models.
It is a variational
method, and consists of special homotopies (they are shortest paths with respect to Willmore energy
); contrast with Thurston's corrugations, which are generic.
The original method of half-way models was not optimal: the regular homotopies passed through the midway models, but the path from the round sphere to the midway model was constructed by hand, and was not gradient ascent/descent.
Eversions via half-way models are called tobacco-pouch eversions by Francis and Morin.
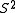in 
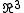, which is so-called because it is the half-way point of a sphere eversion. This class of eversions has time symmetry: the first half of the regular homotopy goes from the standard round sphere to the half-way model, and the second half (which goes from the half-way model to the inside-out sphere) is the same process in reverse.
on the space of all immersions of the sphere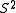
in 
.
The round sphere and the inside-out round sphere are the unique global minima for Willmore energy, and a minimax eversion is a path connecting these by passing over a saddle point
(like traveling between two valleys via a mountain pass).
Kusner's half-way models are saddle point
s for Willmore energy, arising (according to a theorem of Bryant) from certain complete minimal surfaces in 3-space; the minimax eversions consist of gradient ascent from the round sphere to the half-way model, then gradient descent down (gradient descent for Willmore energy is called Willmore flow). More symmetrically, start at the half-way model; push in one direction and follow Willmore flow down to a round sphere; push in the opposite direction and follow Willmore flow down to the inside-out round sphere.
There are two families of half-way models (this observation is due to Francis and Morin):
as a half-way model. Later Morin discovered the Morin surface
and used it to construct other sphere eversions. Kusner conceived the minimax eversions in the early 1980s: historical details.
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, minimax eversions are a class of sphere eversions, constructed by using half-way models.
It is a variational
Calculus of variations
Calculus of variations is a field of mathematics that deals with extremizing functionals, as opposed to ordinary calculus which deals with functions. A functional is usually a mapping from a set of functions to the real numbers. Functionals are often formed as definite integrals involving unknown...
method, and consists of special homotopies (they are shortest paths with respect to Willmore energy
Willmore energy
In differential geometry, the Willmore energy is a quantitative measure of how much a given surface deviates from a round sphere. Mathematically, the Willmore energy of a smooth closed surface embedded in three-dimensional Euclidean space is defined to be the integral of the mean curvature squared...
); contrast with Thurston's corrugations, which are generic.
The original method of half-way models was not optimal: the regular homotopies passed through the midway models, but the path from the round sphere to the midway model was constructed by hand, and was not gradient ascent/descent.
Eversions via half-way models are called tobacco-pouch eversions by Francis and Morin.
Half-way models
A half-way model is an immersion of the sphere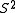 in 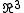, which is so-called because it is the half-way point of a sphere eversion. This class of eversions has time symmetry: the first half of the regular homotopy goes from the standard round sphere to the half-way model, and the second half (which goes from the half-way model to the inside-out sphere) is the same process in reverse.Explanation
Rob Kusner proposed optimal eversions using the Willmore energyWillmore energy
In differential geometry, the Willmore energy is a quantitative measure of how much a given surface deviates from a round sphere. Mathematically, the Willmore energy of a smooth closed surface embedded in three-dimensional Euclidean space is defined to be the integral of the mean curvature squared...
on the space of all immersions of the sphere
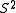in .The round sphere and the inside-out round sphere are the unique global minima for Willmore energy, and a minimax eversion is a path connecting these by passing over a saddle point
Saddle point
In mathematics, a saddle point is a point in the domain of a function that is a stationary point but not a local extremum. The name derives from the fact that in two dimensions the surface resembles a saddle that curves up in one direction, and curves down in a different direction...
(like traveling between two valleys via a mountain pass).
Kusner's half-way models are saddle point
Saddle point
In mathematics, a saddle point is a point in the domain of a function that is a stationary point but not a local extremum. The name derives from the fact that in two dimensions the surface resembles a saddle that curves up in one direction, and curves down in a different direction...
s for Willmore energy, arising (according to a theorem of Bryant) from certain complete minimal surfaces in 3-space; the minimax eversions consist of gradient ascent from the round sphere to the half-way model, then gradient descent down (gradient descent for Willmore energy is called Willmore flow). More symmetrically, start at the half-way model; push in one direction and follow Willmore flow down to a round sphere; push in the opposite direction and follow Willmore flow down to the inside-out round sphere.
There are two families of half-way models (this observation is due to Francis and Morin):
- odd order: generalizing Boy's surfaceBoy's surfaceIn geometry, Boy's surface is an immersion of the real projective plane in 3-dimensional space found by Werner Boy in 1901...
: 3-fold, 5-fold, etc., symmetry; half-way model is a double-covered projective planeProjective planeIn mathematics, a projective plane is a geometric structure that extends the concept of a plane. In the ordinary Euclidean plane, two lines typically intersect in a single point, but there are some pairs of lines that do not intersect...
(generically 2-1 immersed sphere). - even order: generalizing Morin surfaceMorin surfaceThe Morin surface is the half-way model of the sphere eversion discovered by Bernard Morin. It features fourfold rotational symmetry.If the original sphere to be everted has its outer surface colored green and its inner surface colored red, then when the sphere is transformed through homotopy into...
: 2-fold, 4-fold, etc., symmetry; half-way model is a generically 1-1 immersed sphere, and a twist by half a symmetry interchanges sheets of the sphere
History
The first explicit sphere eversion was by Shapiro and Phillips in the early 1960s, using Boy's surfaceBoy's surface
In geometry, Boy's surface is an immersion of the real projective plane in 3-dimensional space found by Werner Boy in 1901...
as a half-way model. Later Morin discovered the Morin surface
Morin surface
The Morin surface is the half-way model of the sphere eversion discovered by Bernard Morin. It features fourfold rotational symmetry.If the original sphere to be everted has its outer surface colored green and its inner surface colored red, then when the sphere is transformed through homotopy into...
and used it to construct other sphere eversions. Kusner conceived the minimax eversions in the early 1980s: historical details.