Inverse mean curvature flow
Encyclopedia
In the field of differential geometry in mathematics
, inverse mean curvature flow (IMCF) is an example of a geometric flow of hypersurface
s a Riemannian manifold
(for example, smooth surfaces in 3-dimensional Euclidean space). Intuitively, a family of surfaces evolves under IMCF if the outward normal speed at which a point on the surface moves is given by the reciprocal of the mean curvature
of the surface. For example, a round sphere evolves under IMCF by expanding outward uniformly at an exponentially growing rate (see below). In general, this flow does not exist (for example, if a point on the surface has zero mean curvature), and even if it does, it generally develops singularities. Nevertheless, it has recently been an important tool in differential geometry and mathematical problems in general relativity
.
of radius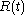
evolving under IMCF in 3-dimensional Euclidean space
, where
is the time parameter of the flow. (By symmetry considerations, a round sphere will remain round under this flow, so that the radius at time 
determines the surface at time 
.) The outward speed under the flow is the derivative,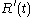 
, and the mean curvature equals 
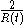. (This may be computed from the first variation of area formula
.) Setting the speed equal to the reciprocal of the mean curvature, we have the ordinary differential equation
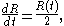
which possesses a unique, smooth solution given by
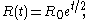
where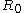
is the radius of the sphere at time 
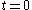. Thus, in this case we see that a round sphere evolves under IMCF by uniformly expanding outward with an exponentially increasing radius.
to IMCF. Geometrically, this means that the flow can be continued past singularities if the surface is allowed to "jump" outward at certain times.
, then a certain geometric quantity associated to the surface, the Hawking mass, is non-decreasing under the flow. Amazingly, the Hawking mass is non-decreasing even under IMCF in the sense of Huisken and Ilmanen. This fact is at the heart of the geometric applications of IMCF.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, inverse mean curvature flow (IMCF) is an example of a geometric flow of hypersurface
Hypersurface
In geometry, a hypersurface is a generalization of the concept of hyperplane. Suppose an enveloping manifold M has n dimensions; then any submanifold of M of n − 1 dimensions is a hypersurface...
s a Riemannian manifold
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
(for example, smooth surfaces in 3-dimensional Euclidean space). Intuitively, a family of surfaces evolves under IMCF if the outward normal speed at which a point on the surface moves is given by the reciprocal of the mean curvature
Mean curvature
In mathematics, the mean curvature H of a surface S is an extrinsic measure of curvature that comes from differential geometry and that locally describes the curvature of an embedded surface in some ambient space such as Euclidean space....
of the surface. For example, a round sphere evolves under IMCF by expanding outward uniformly at an exponentially growing rate (see below). In general, this flow does not exist (for example, if a point on the surface has zero mean curvature), and even if it does, it generally develops singularities. Nevertheless, it has recently been an important tool in differential geometry and mathematical problems in general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
.
Example: a round sphere
Consider a two-dimensional sphereSphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
of radius
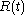evolving under IMCF in 3-dimensional Euclidean spaceEuclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
, where
is the time parameter of the flow. (By symmetry considerations, a round sphere will remain round under this flow, so that the radius at time determines the surface at time .) The outward speed under the flow is the derivative, 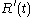, and the mean curvature equals 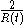. (This may be computed from the first variation of area formulaFirst variation of area formula
In Riemannian geometry, the first variation of area formula relates the mean curvature of a hypersurface to the rate of change of its area as it evolves in the outward normal direction....
.) Setting the speed equal to the reciprocal of the mean curvature, we have the ordinary differential equation
Ordinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
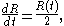
which possesses a unique, smooth solution given by
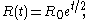
where
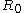is the radius of the sphere at time 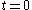. Thus, in this case we see that a round sphere evolves under IMCF by uniformly expanding outward with an exponentially increasing radius.Generalization: weak IMCF
In 1997 G. Huisken and T. Ilmanen showed that it makes sense to define a weak solutionWeak solution
In mathematics, a weak solution to an ordinary or partial differential equation is a function for which the derivatives may not all exist but which is nonetheless deemed to satisfy the equation in some precisely defined sense. There are many different definitions of weak solution, appropriate for...
to IMCF. Geometrically, this means that the flow can be continued past singularities if the surface is allowed to "jump" outward at certain times.
Monotonicity of the Hawking mass
It was observed by Geroch, Jang, and Wald that if a closed, connected surface evolves smoothly under IMCF in a 3-manifold with nonnegative scalar curvatureScalar curvature
In Riemannian geometry, the scalar curvature is the simplest curvature invariant of a Riemannian manifold. To each point on a Riemannian manifold, it assigns a single real number determined by the intrinsic geometry of the manifold near that point...
, then a certain geometric quantity associated to the surface, the Hawking mass, is non-decreasing under the flow. Amazingly, the Hawking mass is non-decreasing even under IMCF in the sense of Huisken and Ilmanen. This fact is at the heart of the geometric applications of IMCF.
Applications
In the late 1990s and early 2000s, weak IMCF has been used to- prove the Riemannian Penrose inequalityRiemannian Penrose inequalityIn mathematical general relativity, the Penrose inequality, first conjectured by Sir Roger Penrose, estimates the mass of a spacetime in terms of the total area of its black holes and is a generalization of the positive mass theorem. The Riemannian Penrose inequality is the most important special...
for the case of a single black hole (due to Huisken and Ilmanen) - compute the Yamabe invariantYamabe invariantIn mathematics, in the field of differential geometry, the Yamabe invariant is a real number invariant associated to a smooth manifold that is preserved under diffeomorphisms. It was first written down independently by O. Kobayashi and R. Schoen and takes its name from H...
of three-dimensional real projective spaceReal projective spaceIn mathematics, real projective space, or RPn, is the topological space of lines through 0 in Rn+1. It is a compact, smooth manifold of dimension n, and a special case of a Grassmannian.-Construction:...
(due to H. Bray and A. Neves)