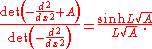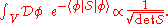
Functional determinant
Encyclopedia
In mathematics
, if S is a linear operator mapping a function space
V to itself, it is sometimes possible to define an infinite-dimensional generalization of the determinant
. The corresponding quantity det(S) is called the functional determinant of S.
There are several formulas for the functional determinant. They are all based on the fact that, for diagonalizable finite-dimensional matrices, the determinant is equal to the product of the eigenvalues. A mathematically rigorous definition is via the zeta function of the operator,
where tr stands for the functional trace
: the determinant is then defined by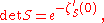
where the zeta function in the point s = 0 is defined by analytic continuation
. Another possible generalization, often used by physicists when using the Feynman path integral formalism in quantum field theory
, uses a functional integration
:
This path integral is only well defined up to some divergent multiplicative constant. In order to give it a rigorous meaning, it must be divided by another functional determinant, making the spurious constants cancel.
These are now, ostensibly, two different definitions for the functional determinant, one coming from quantum field theory and one coming from spectral theory. Each involves some kind of regularization: in the definition popular in physics, two determinants can only be compared with one another; in mathematics, the zeta function was used. have shown that the results obtained by comparing two functional determinants in the QFT formalism agree with the results obtained by the zeta functional determinant.
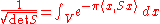
holds.
The problem is to find a way to make sense of the determinant of an operator S on an infinite dimensional function space. One approach, favored in quantum field theory, in which the function space consists of continuous paths on a closed interval, is to formally attempt to calculate the integral
where V is the function space and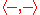
the L2 inner product, and 
the Wiener measure. The basic assumption on S is that it should be selfadjoint, and have discrete spectrum λ1, λ2, λ3… with a corresponding set of eigenfunctions f1, f2, f3… which are complete in L2
(as would, for example, be the case for the second derivative operator on a compact interval Ω). This roughly means all functions φ can be written as linear combination
s of the functions fi:
Hence the inner product in the exponential can be written as
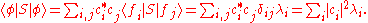
In the basis of the functions fi, the functional integration reduces to an integration over all basisfunctions. Formally, assuming our intuition from the finite dimensional case carries over into the infinite dimensional setting, the measure should then be equal to
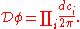
This makes the functional integral a product of Gaussian integral
s:
The integrals can then be evaluated, giving
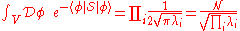
where N is an infinite constant that needs to be dealt with by some regularization procedure. The product of all eigenvalues is equal to the determinant for finite-dimensional spaces, and we formally define this to be the case in our infinite-dimensional case also. This results in the formula
If all quantities converge in an appropriate sense, then the functional determinant can be described as a classical limit (Watson and Whittaker). Otherwise, it is necessary to perform some kind of regularization
. The most popular of which for computing functional determinants is the zeta function regularization
. For instance, this allows for the computation of the determinant of the Laplace and Dirac operators on a Riemannian manifold
, using the Minakshisundaram–Pleijel zeta function. Otherwise, it is also possible to consider the quotient of two determinants, making the divergent constants cancel.
with smooth coefficients which is positive on functions of compact support. That is, there exists a constant c > 0 such that
for all compactly supported smooth functions φ. Then S has a self-adjoint extension to an operator on L2 with lower bound c. The eigenvalues of S can be arranged in a sequence
Then the zeta function of S is defined by the series: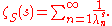
It is known that ζS has a meromorphic extension to the entire plane. Moreover, although one can define the zeta function in more general situations, the zeta function of an elliptic differential operator (or pseudodifferential operator) is regular at
.
Formally, differentiating this series term-by-term gives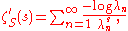
and so if the functional determinant is well-defined, then it should be given by
Since the analytic continuation of the zeta function is regular at zero, this can be rigorously adopted as a definition of the determinant.
This kind of Zeta-regularized functional determinant also appears when evaluating sums of the form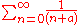
, integration over 'a' gives 
which it just can be considered as the logarithm of the determinant for an Harmonic oscillator
this last value is just equal to
, where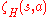 
is the Hurwitz Zeta function
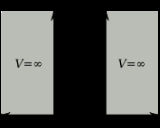
particle in an infinite potential well
:
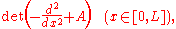
where A is the depth of the potential and L is the length of the well. We will compute this determinant by diagonalizing the operator and multiplying the eigenvalues. So as not to have to bother with the uninteresting divergent constant, we will compute the quotient between the determinants of the operator with depth A and the operator with depth A = 0. The eigenvalues of this potential are equal to
This means that
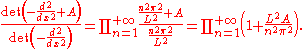
Now we can use Euler
's infinite product representation for the sine function:
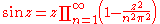
from which a similar formula for the hyperbolic sine function
can be derived:
Applying this, we find that
where m is a complex
constant. This expression is a meromorphic function
of m, having zeros when m equals an eigenvalue of the operator with potential V1(x) and a pole when m is an eigenvalue of the operator with potential V2(x). We now consider the functions ψm1 and ψm2 with
obeying the boundary conditions
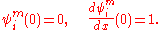
If we construct the function
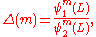
which is also a meromorphic function of m, we see that it has exactly the same poles and zeroes as the quotient of determinants we are trying to compute: if m is an eigenfunction of the operator number one, then ψm1(x) will be an eigenfunction thereof, meaning ψm1(L) = 0; and analogously for the numerator. By Liouville's theorem
, two meromorphic functions with the same zeros and poles must be proportional to one another. In our case, the proportionality constant turns out to be one, and we get
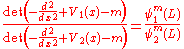
for all values of m. For m = 0 we get
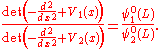
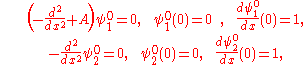
yielding the following solutions:
This gives the final expression
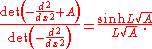
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, if S is a linear operator mapping a function space
Function space
In mathematics, a function space is a set of functions of a given kind from a set X to a set Y. It is called a space because in many applications it is a topological space, a vector space, or both.-Examples:...
V to itself, it is sometimes possible to define an infinite-dimensional generalization of the determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
. The corresponding quantity det(S) is called the functional determinant of S.
There are several formulas for the functional determinant. They are all based on the fact that, for diagonalizable finite-dimensional matrices, the determinant is equal to the product of the eigenvalues. A mathematically rigorous definition is via the zeta function of the operator,
where tr stands for the functional trace
Trace class
In mathematics, a trace class operator is a compact operator for which a trace may be defined, such that the trace is finite and independent of the choice of basis....
: the determinant is then defined by
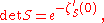
where the zeta function in the point s = 0 is defined by analytic continuation
Analytic continuation
In complex analysis, a branch of mathematics, analytic continuation is a technique to extend the domain of a given analytic function. Analytic continuation often succeeds in defining further values of a function, for example in a new region where an infinite series representation in terms of which...
. Another possible generalization, often used by physicists when using the Feynman path integral formalism in quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
, uses a functional integration
Functional integration
Functional integration is a collection of results in mathematics and physics where the domain of an integral is no longer a region of space, but a space of functions...
:
This path integral is only well defined up to some divergent multiplicative constant. In order to give it a rigorous meaning, it must be divided by another functional determinant, making the spurious constants cancel.
These are now, ostensibly, two different definitions for the functional determinant, one coming from quantum field theory and one coming from spectral theory. Each involves some kind of regularization: in the definition popular in physics, two determinants can only be compared with one another; in mathematics, the zeta function was used. have shown that the results obtained by comparing two functional determinants in the QFT formalism agree with the results obtained by the zeta functional determinant.
Path integral version
For a positive selfadjoint operator S on a finite-dimensional Euclidean space V, the formula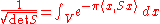holds.
The problem is to find a way to make sense of the determinant of an operator S on an infinite dimensional function space. One approach, favored in quantum field theory, in which the function space consists of continuous paths on a closed interval, is to formally attempt to calculate the integral
where V is the function space and
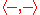the L2 inner product, and the Wiener measure. The basic assumption on S is that it should be selfadjoint, and have discrete spectrum λ1, λ2, λ3… with a corresponding set of eigenfunctions f1, f2, f3… which are complete in L2Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
(as would, for example, be the case for the second derivative operator on a compact interval Ω). This roughly means all functions φ can be written as linear combination
Linear combination
In mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...
s of the functions fi:
Hence the inner product in the exponential can be written as
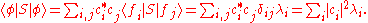
In the basis of the functions fi, the functional integration reduces to an integration over all basisfunctions. Formally, assuming our intuition from the finite dimensional case carries over into the infinite dimensional setting, the measure should then be equal to
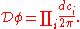
This makes the functional integral a product of Gaussian integral
Gaussian integral
The Gaussian integral, also known as the Euler-Poisson integral or Poisson integral, is the integral of the Gaussian function e−x2 over the entire real line.It is named after the German mathematician and...
s:
The integrals can then be evaluated, giving
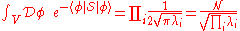
where N is an infinite constant that needs to be dealt with by some regularization procedure. The product of all eigenvalues is equal to the determinant for finite-dimensional spaces, and we formally define this to be the case in our infinite-dimensional case also. This results in the formula
If all quantities converge in an appropriate sense, then the functional determinant can be described as a classical limit (Watson and Whittaker). Otherwise, it is necessary to perform some kind of regularization
Divergent series
In mathematics, a divergent series is an infinite series that is not convergent, meaning that the infinite sequence of the partial sums of the series does not have a limit....
. The most popular of which for computing functional determinants is the zeta function regularization
Zeta function regularization
In mathematics and theoretical physics, zeta function regularization is a type of regularization or summability method that assigns finite values to divergent sums or products, and in particular can be used to define determinants and traces of some self-adjoint operators...
. For instance, this allows for the computation of the determinant of the Laplace and Dirac operators on a Riemannian manifold
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
, using the Minakshisundaram–Pleijel zeta function. Otherwise, it is also possible to consider the quotient of two determinants, making the divergent constants cancel.
Zeta function version
Let S be an elliptic differential operatorDifferential operator
In mathematics, a differential operator is an operator defined as a function of the differentiation operator. It is helpful, as a matter of notation first, to consider differentiation as an abstract operation, accepting a function and returning another .This article considers only linear operators,...
with smooth coefficients which is positive on functions of compact support. That is, there exists a constant c > 0 such that
for all compactly supported smooth functions φ. Then S has a self-adjoint extension to an operator on L2 with lower bound c. The eigenvalues of S can be arranged in a sequence
Then the zeta function of S is defined by the series:
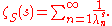
It is known that ζS has a meromorphic extension to the entire plane. Moreover, although one can define the zeta function in more general situations, the zeta function of an elliptic differential operator (or pseudodifferential operator) is regular at
.Formally, differentiating this series term-by-term gives
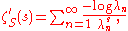
and so if the functional determinant is well-defined, then it should be given by
Since the analytic continuation of the zeta function is regular at zero, this can be rigorously adopted as a definition of the determinant.
This kind of Zeta-regularized functional determinant also appears when evaluating sums of the form
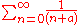, integration over 'a' gives which it just can be considered as the logarithm of the determinant for an Harmonic oscillatorHarmonic oscillator
In classical mechanics, a harmonic oscillator is a system that, when displaced from its equilibrium position, experiences a restoring force, F, proportional to the displacement, x: \vec F = -k \vec x \, where k is a positive constant....
this last value is just equal to
, where 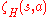is the Hurwitz Zeta functionPractical example
The infinite potential well
We will compute the determinant of the following operator describing the motion of a quantum mechanicalQuantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
particle in an infinite potential well
Particle in a box
In quantum mechanics, the particle in a box model describes a particle free to move in a small space surrounded by impenetrable barriers. The model is mainly used as a hypothetical example to illustrate the differences between classical and quantum systems...
:
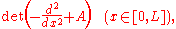
where A is the depth of the potential and L is the length of the well. We will compute this determinant by diagonalizing the operator and multiplying the eigenvalues. So as not to have to bother with the uninteresting divergent constant, we will compute the quotient between the determinants of the operator with depth A and the operator with depth A = 0. The eigenvalues of this potential are equal to
This means that
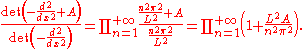
Now we can use Euler
Leonhard Euler
Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
's infinite product representation for the sine function:
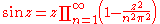
from which a similar formula for the hyperbolic sine function
Hyperbolic function
In mathematics, hyperbolic functions are analogs of the ordinary trigonometric, or circular, functions. The basic hyperbolic functions are the hyperbolic sine "sinh" , and the hyperbolic cosine "cosh" , from which are derived the hyperbolic tangent "tanh" and so on.Just as the points form a...
can be derived:
Applying this, we find that
Another way for computing the functional determinant
For one-dimensional potentials, a short-cut yielding the functional determinant exists. It is based on consideration of the following expression:where m is a complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
constant. This expression is a meromorphic function
Meromorphic function
In complex analysis, a meromorphic function on an open subset D of the complex plane is a function that is holomorphic on all D except a set of isolated points, which are poles for the function...
of m, having zeros when m equals an eigenvalue of the operator with potential V1(x) and a pole when m is an eigenvalue of the operator with potential V2(x). We now consider the functions ψm1 and ψm2 with
obeying the boundary conditions
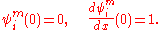
If we construct the function
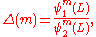
which is also a meromorphic function of m, we see that it has exactly the same poles and zeroes as the quotient of determinants we are trying to compute: if m is an eigenfunction of the operator number one, then ψm1(x) will be an eigenfunction thereof, meaning ψm1(L) = 0; and analogously for the numerator. By Liouville's theorem
Liouville's theorem (complex analysis)
In complex analysis, Liouville's theorem, named after Joseph Liouville, states that every bounded entire function must be constant. That is, every holomorphic function f for which there exists a positive number M such that |f| ≤ M for all z in C is constant.The theorem is considerably improved by...
, two meromorphic functions with the same zeros and poles must be proportional to one another. In our case, the proportionality constant turns out to be one, and we get
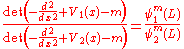
for all values of m. For m = 0 we get
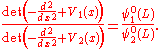
The infinite potential well revisited
The problem in the previous section can be solved more easily with this formalism. The functions ψ0i(x) obey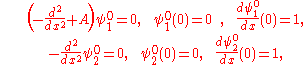yielding the following solutions:
This gives the final expression