
Fraunhofer diffraction (mathematics)
Encyclopedia
In optics
, the Fraunhofer diffraction equation is used to model the diffraction
of waves when the diffraction pattern is viewed at a long distance from the diffracting object, and also when it is viewed at the focal plane of an imaging lens
.
The equation was named in honour of Joseph von Fraunhofer
although he was not actually involved in the development of the theory.
This article gives the equation in various mathematical forms, and provides detailed calculations of the Fraunhofer diffraction pattern for several different forms of diffacting aperures. A qualitative discussion of Fraunhofer diffraction can be found here
.
Fraunhofer diffraction equation=
When a beam of light is partly blocked by an obstacle, some of the light is scattered around the object, and light and dark bands are often seen at the edge of the shadow - this effect is known as diffraction. The Kirchhoff diffraction equation
provides an expression, derived from the wave equation
, which describes the wave diffracted by an aperture; analytical solutions to this equation are not available for most configurations.
The Fraunhofer diffraction equation is an approximation which can be applied when the diffracted wave is observed in the far field, and also when a lens is used to focus the diffracted light; in many instances, a simple analytical solution is available to the Fraunhofer equation - several of these are derived below.
λ, wavenumber
with complex amplitude , and the diffracted wave is observed in the plane where are the direction cosines of the point with respect to the origin, the complex amplitude of the diffracted wave is given by the Fraunhofer diffraction equation as:
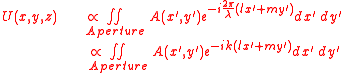
It can be seen from this equation that the form of the diffraction pattern depends only on the direction of viewing, so the diffraction pattern changes in size but not in form with change of viewing distance.
The Fraunhofer diffraction equation can be expressed in a variety of mathematically equivalent forms. For example: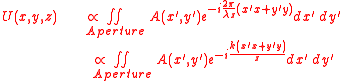
It can be seen that the integral in the above equations is the Fourier transform
of the aperture function evaluated at frequencies.

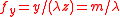
Thus, we can also write the equation in terms of a Fourier transform
as:
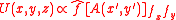
where is the Fourier transform of . The Fourier transform formulation can be very useful in solving diffraction problems.
Another form is:

where represent the observation point and a point in the aperture respectively, and represent the wave vector
s of the disturbance at the aperture and of the diffracted waves respectively, and represents the magnitude
of the disturbance at the aperture.
rather than Cartesian co-ordinates.
A point in the aperture has co-oordinates giving:

and

The complex amplitude at is given by , and the area converts to ρ' dρ' dω', giving

Using the integral representation of the Bessel
function: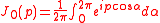
we have
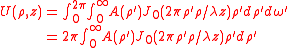
where the integration over gives since the equation is circularly symmetric, i.e. there is no dependence on .
In this case, we have equal to the Fourier-Bessel or Hankel transform of the aperture function,
Examples of Fraunhofer diffraction with a normally incident monochromatic plane wave =
In each case, the diffracting object is located in the z=0 plane, and the complex amplitude of the incident plane wave
is given by
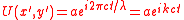
where
and the phase
is zero at time = 0.
The time dependent factor is omitted throughout the calculations, as it remains constant, and is averaged out when the intensity is calculated. The intensity at is propotional to the amplitude times its complex conjugate
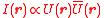
These derivations can be found in most standard optics books, in slightly different forms using varying notations. A reference is given for each of the systems modelled here. The Fourier transforms used can be found here.
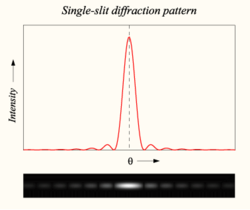 The aperture is a slit of width which is located along the -axis,
The aperture is a slit of width which is located along the -axis,
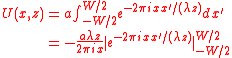
Using Euler's formula
, this can be simplified to:
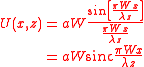
where . It should be noted that the sinc function is sometimes defined as and this may cause confusion when looking at derivations in different texts.
This can also be written as:

where is the angle between z-axis and the line joining x to the origin and .
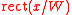
The Fourier transform of this function is given by
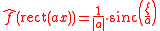
where is the Fourier transform frequency, and the function is here defined as sin(πx)/(πx)
The Fourier transform frequency here is , giving
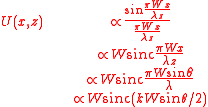
Note that the function is here defined as sin(π)/(x) to maintain consistency.
is proportional to the square of the amplitude, and is then
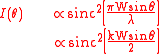
of wavelength λ, the complex amplitude can be found using similar analyses to those in the previous section, applied over two independent dimensions as: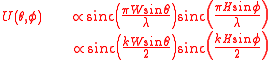
The intensity is given by
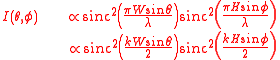
where and are the angles between the and axes and the and axes, respectively.
In practice, all slits are of finite length and will therefore produce diffraction on both directions. If the length of the slit is much greater than its width, then the spacing of the horizontal diffraction fringes will be much less than the spacing of the vertical fringes. If the illuminating beam does not illuminate the whole length of the slit, the spacing of the horizontal fringes is determined by the dimensions of the laser beam. Close examination of the two-slit pattern below shows that there are very fine horizontal diffraction fringes above and below the main spot, as well as the more obvious vertical fringes.
 The aperture has diameter . The complex amplitude in the observation plane is given by
The aperture has diameter . The complex amplitude in the observation plane is given by

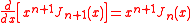
to give

If we substitute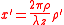
and the limits of the integration become 0 and , we get
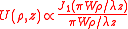
Putting = sin , we get
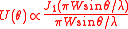

The Fourier-Bessel transform for this function is given by the relationship

where is the transform frequency which is equal to and = .
Thus, we get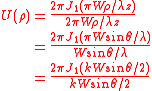
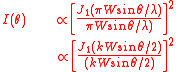
The diffracted pattern is symmetric about the normal axis.

giving
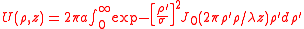
transform is defined as

where Jν is the Bessel function
of the first kind of order ν with ν ≥ −1/2.
The Hankel transform is
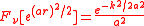
giving

and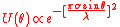
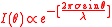
This function is plotted on the right, and it can be seen that, unlike the diffraction patterns produced by rectangular or circular apertures, it has no secondary rings. This can be used in a process called apodization
- the aperture is covered by a filter whose transmission varies as a Gaussian function, giving a diffraction pattern with no secondary rings.:
, and secondly because of its role as a thought experiment in Double-slit experiment
in quantum mechanics.
 Assume we have two long slits illuminated by a plane wave of wavelength . The slits are in the plane, parallel to the axis, separated by a distance and are symmetrical about the origin. The width of the slits is small compared with the wavelength.
Assume we have two long slits illuminated by a plane wave of wavelength . The slits are in the plane, parallel to the axis, separated by a distance and are symmetrical about the origin. The width of the slits is small compared with the wavelength.
The complex amplitude of the summed waves is given by:
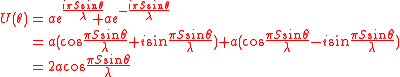

where is the delta function.
We have

and
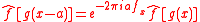
giving
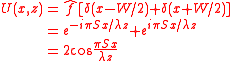
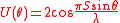
This is the same expression as that derived above by integration.
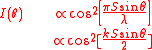
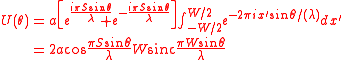
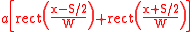
The Fourier transform of this function is given by
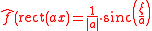
where is the Fourier transform frequency, and the function is here defined as sin(πx)/(πx)
and
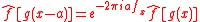
We have
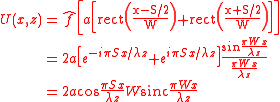
or
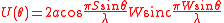
This is the same expression as was derived by integration.
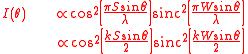
It can be seen that the form of the intensity pattern is the product of the individual slit diffraction pattern, and the interfernce pattern which would be obtained with slits of negligible width. This is illustrated in the image at the right which shows single slit diffraction by a laser beam, and also the diffraction/interference pattern given by two identical slits.
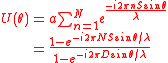
since this is the sum of a geometric series.
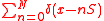
The Fourier transform of this function is:
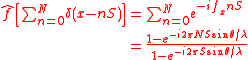
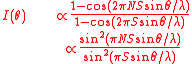
This function has a series of maxima and minima. There are regularly spaced "prinicpal maxima", and a number of much smaller maxima in between the principal maxima. The principal maxima occur when
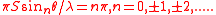
and the main diffracted beams therefore occur at angles:
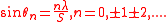
This is the grating equation for normally incident light.
The number of small intermediate maxima is equal to the number of slits, -1 and their size and shape is also determined by .
The form of the pattern for =50 is shown in the first figure .
The detailed structure for 20 and 50 slits gratings are illustrated in the second diagram.
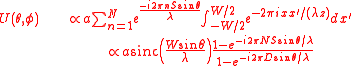

Using the convolution theorem which says that if we have two functions and , and we have
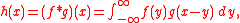
where ∗ denotes the convolution operation, then we also have
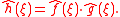
we can write the aperture function as

The amplitude is then given by the Fourier transform of this expression as:
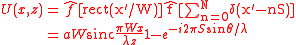

The diagram shows the diffraction pattern for a grating with 20 slits, where the width of the slits is 1/5th of the slit separation. The size of the main diffracted peaks is modulated with the diffraction pattern of the individual slits.
.
Non-normal illumination=
If the aperture is illuminated by a mono-chromatic plane wave incident in a direction , the first version of the Fraunhofer equation above becomes:
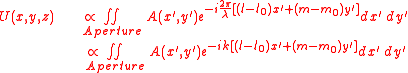
The equations used to model each of the systems above are altered only by changes in the constants multiplying and , so the difffracted light patterns will have the form, except that they will now be centred around the direction of the incident plane wave.
The grating equation becomes
 .
.
Non-monochromatic illumination=
In all of the above examples of Fraunhofer diffraction, the effect of increasing the wavelength of the illuminating light is to reduce the size of the diffraction structure, and conversely, when the wavelength is reduced, the size of the pattern increases. If the light is not mono-chromatic, i.e. it consists of a range of different wavelengths, each wavelength is diffracted into a pattern of a slightly different size to its neighbours. If the spread of wavelengths is significantly smaller than the mean wavelength, the individual patterns will vary very little in size, and so the basic diffraction will still appear with slightly reduced contrast. As the spread of wavelengths is increased, the number of "fringes" which can be observed is reduced.
See also =
Reference sources=
Optics
Optics is the branch of physics which involves the behavior and properties of light, including its interactions with matter and the construction of instruments that use or detect it. Optics usually describes the behavior of visible, ultraviolet, and infrared light...
, the Fraunhofer diffraction equation is used to model the diffraction
Diffraction
Diffraction refers to various phenomena which occur when a wave encounters an obstacle. Italian scientist Francesco Maria Grimaldi coined the word "diffraction" and was the first to record accurate observations of the phenomenon in 1665...
of waves when the diffraction pattern is viewed at a long distance from the diffracting object, and also when it is viewed at the focal plane of an imaging lens
Lens
-Optics:*Lens , an optical element which converges or diverges light**Lens , a part of the eye**Corrective lens for correction of human vision***Contact lens, placed on the cornea of the eye**Photographic lens, a lens designed for use on a camera...
.
The equation was named in honour of Joseph von Fraunhofer
Joseph von Fraunhofer
Joseph von Fraunhofer was a German optician. He is known for the discovery of the dark absorption lines known as Fraunhofer lines in the Sun's spectrum, and for making excellent optical glass and achromatic telescope objectives.-Biography:Fraunhofer was born in Straubing, Bavaria...
although he was not actually involved in the development of the theory.
This article gives the equation in various mathematical forms, and provides detailed calculations of the Fraunhofer diffraction pattern for several different forms of diffacting aperures. A qualitative discussion of Fraunhofer diffraction can be found here
Fraunhofer diffraction
In optics, the Fraunhofer diffraction equation is used to model the diffraction of waves when the diffraction pattern is viewed at a long distance from the diffracting object, and also when it is viewed at the focal plane of an imaging lens....
.
Fraunhofer diffraction equation=
When a beam of light is partly blocked by an obstacle, some of the light is scattered around the object, and light and dark bands are often seen at the edge of the shadow - this effect is known as diffraction. The Kirchhoff diffraction equation
Kirchhoff's diffraction formula
Kirchhoff's diffraction formula can be used to model the propagation of light in a wide range of configurations, either analytically or using numerical modelling. It gives an expression for the wave disturbance when a monochromatic spherical wave passes through an opening in an opaque screen...
provides an expression, derived from the wave equation
Wave equation
The wave equation is an important second-order linear partial differential equation for the description of waves – as they occur in physics – such as sound waves, light waves and water waves. It arises in fields like acoustics, electromagnetics, and fluid dynamics...
, which describes the wave diffracted by an aperture; analytical solutions to this equation are not available for most configurations.
The Fraunhofer diffraction equation is an approximation which can be applied when the diffracted wave is observed in the far field, and also when a lens is used to focus the diffracted light; in many instances, a simple analytical solution is available to the Fraunhofer equation - several of these are derived below.
Cartesian co-ordinates
If the aperture is in plane, with the origin in the aperture and is illuminated by a monochromatic wave, of wavelengthWavelength
In physics, the wavelength of a sinusoidal wave is the spatial period of the wave—the distance over which the wave's shape repeats.It is usually determined by considering the distance between consecutive corresponding points of the same phase, such as crests, troughs, or zero crossings, and is a...
λ, wavenumber
Wavenumber
In the physical sciences, the wavenumber is a property of a wave, its spatial frequency, that is proportional to the reciprocal of the wavelength. It is also the magnitude of the wave vector...
with complex amplitude , and the diffracted wave is observed in the plane where are the direction cosines of the point with respect to the origin, the complex amplitude of the diffracted wave is given by the Fraunhofer diffraction equation as:
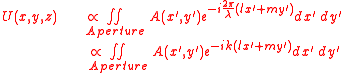
It can be seen from this equation that the form of the diffraction pattern depends only on the direction of viewing, so the diffraction pattern changes in size but not in form with change of viewing distance.
The Fraunhofer diffraction equation can be expressed in a variety of mathematically equivalent forms. For example:
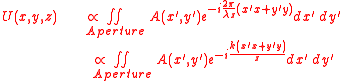
It can be seen that the integral in the above equations is the Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
of the aperture function evaluated at frequencies.

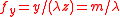
Thus, we can also write the equation in terms of a Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
as:
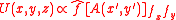
where is the Fourier transform of . The Fourier transform formulation can be very useful in solving diffraction problems.
Another form is:

where represent the observation point and a point in the aperture respectively, and represent the wave vector
Wave vector
In physics, a wave vector is a vector which helps describe a wave. Like any vector, it has a magnitude and direction, both of which are important: Its magnitude is either the wavenumber or angular wavenumber of the wave , and its direction is ordinarily the direction of wave propagation In...
s of the disturbance at the aperture and of the diffracted waves respectively, and represents the magnitude
Magnitude
Magnitude Is A Part Of An EarthquakesMagnitude may refer to:In mathematics:*Magnitude , the relative size of a mathematical object*Magnitude , a term for the size or length of a vector...
of the disturbance at the aperture.
Polar co-ordinates
When the diffracting aperture has circular symmetry, it is useful to use polarPolar
- Science, technology, and mathematics :*Polar , a satellite launched by NASA in 1996*Polar , a strongly magnetic cataclysmic variable star system...
rather than Cartesian co-ordinates.
A point in the aperture has co-oordinates giving:

and

The complex amplitude at is given by , and the area converts to ρ' dρ' dω', giving

Using the integral representation of the Bessel
Bessel
Bessel may refer to:* Bessel beam* Bessel ellipsoid* Bessel function in mathematics* Bessel's inequality in mathematics* Bessel filter, a linear filter often used in audio crossover systems* Bessel , a small lunar crater...
function:
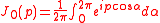
we have
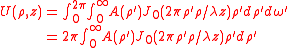
where the integration over gives since the equation is circularly symmetric, i.e. there is no dependence on .
In this case, we have equal to the Fourier-Bessel or Hankel transform of the aperture function,
Examples of Fraunhofer diffraction with a normally incident monochromatic plane wave =
In each case, the diffracting object is located in the z=0 plane, and the complex amplitude of the incident plane wave
Plane wave
In the physics of wave propagation, a plane wave is a constant-frequency wave whose wavefronts are infinite parallel planes of constant peak-to-peak amplitude normal to the phase velocity vector....
is given by
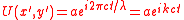
where
- is the magnitudeMagnitudeMagnitude Is A Part Of An EarthquakesMagnitude may refer to:In mathematics:*Magnitude , the relative size of a mathematical object*Magnitude , a term for the size or length of a vector...
of the wave disturbance, - is the wavelength,
- is the velocity of light,
- is the time
- = is the wave number
and the phase
Phase
-In physics:*Phase , a physically distinctive form of a substance, such as the solid, liquid, and gaseous states of ordinary matter**Phase transition is the transformation of a thermodynamic system from one phase to another*Phase...
is zero at time = 0.
The time dependent factor is omitted throughout the calculations, as it remains constant, and is averaged out when the intensity is calculated. The intensity at is propotional to the amplitude times its complex conjugate
Complex conjugate
In mathematics, complex conjugates are a pair of complex numbers, both having the same real part, but with imaginary parts of equal magnitude and opposite signs...
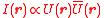
These derivations can be found in most standard optics books, in slightly different forms using varying notations. A reference is given for each of the systems modelled here. The Fourier transforms used can be found here.
Slit of infinite depth

Solution by integration
Assuming the centre of the slit is located at , the first equation above, for all values of , is: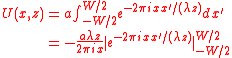
Using Euler's formula
Euler's formula
Euler's formula, named after Leonhard Euler, is a mathematical formula in complex analysis that establishes the deep relationship between the trigonometric functions and the complex exponential function...
, this can be simplified to:
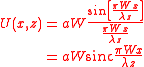
where . It should be noted that the sinc function is sometimes defined as and this may cause confusion when looking at derivations in different texts.
This can also be written as:

where is the angle between z-axis and the line joining x to the origin and .
Fourier transform solution
The slit can be represented by the rect function as: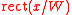
The Fourier transform of this function is given by
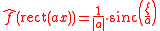
where is the Fourier transform frequency, and the function is here defined as sin(πx)/(πx)
The Fourier transform frequency here is , giving
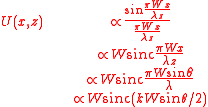
Note that the function is here defined as sin(π)/(x) to maintain consistency.
Intensity
The intensityIntensity (physics)
In physics, intensity is a measure of the energy flux, averaged over the period of the wave. The word "intensity" here is not synonymous with "strength", "amplitude", or "level", as it sometimes is in colloquial speech...
is proportional to the square of the amplitude, and is then
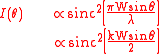
Rectangular aperture
When a slit of width W and height H is illuminated normally by a monochromatic plane wavePlane wave
In the physics of wave propagation, a plane wave is a constant-frequency wave whose wavefronts are infinite parallel planes of constant peak-to-peak amplitude normal to the phase velocity vector....
of wavelength λ, the complex amplitude can be found using similar analyses to those in the previous section, applied over two independent dimensions as:
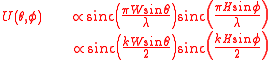
The intensity is given by
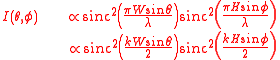
where and are the angles between the and axes and the and axes, respectively.
In practice, all slits are of finite length and will therefore produce diffraction on both directions. If the length of the slit is much greater than its width, then the spacing of the horizontal diffraction fringes will be much less than the spacing of the vertical fringes. If the illuminating beam does not illuminate the whole length of the slit, the spacing of the horizontal fringes is determined by the dimensions of the laser beam. Close examination of the two-slit pattern below shows that there are very fine horizontal diffraction fringes above and below the main spot, as well as the more obvious vertical fringes.
Circular aperture


Solution by integration
Using the recurrence relationship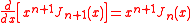
to give

If we substitute
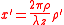
and the limits of the integration become 0 and , we get
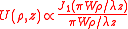
Putting = sin , we get
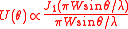
Solution using Fourier Bessel Transform
We can write the aperture function as a step functionStep function
In mathematics, a function on the real numbers is called a step function if it can be written as a finite linear combination of indicator functions of intervals...

The Fourier-Bessel transform for this function is given by the relationship

where is the transform frequency which is equal to and = .
Thus, we get
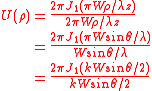
Intensity
The intensity is given by: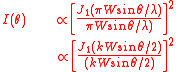
Form of the diffraction pattern
This known as the Airy diffraction patternThe diffracted pattern is symmetric about the normal axis.
Aperture with a gaussian profile
An aperture with a Gaussian profile, for example, a photographic slide whose transmission has a Gaussian variation, so that the amplitude at a point in the aperture located at a distance r from the origin is given by
giving
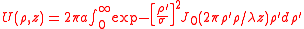
Solution using Fourier-Bessel transform
The Fourier Bessel or HankelHankel transform
In mathematics, the Hankel transform expresses any given function f as the weighted sum of an infinite number of Bessel functions of the first kind Jν. The Bessel functions in the sum are all of the same order ν, but differ in a scaling factor k along the r-axis...
transform is defined as

where Jν is the Bessel function
Bessel function
In mathematics, Bessel functions, first defined by the mathematician Daniel Bernoulli and generalized by Friedrich Bessel, are canonical solutions y of Bessel's differential equation:...
of the first kind of order ν with ν ≥ −1/2.
The Hankel transform is
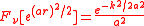
giving

and
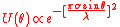
Intensity
The intensity is given by: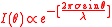
This function is plotted on the right, and it can be seen that, unlike the diffraction patterns produced by rectangular or circular apertures, it has no secondary rings. This can be used in a process called apodization
Apodization
Apodization literally means "removing the foot". It is the technical term for changing the shape of a mathematical function, an electrical signal, an optical transmission or a mechanical structure.- Apodization in signal processing :...
- the aperture is covered by a filter whose transmission varies as a Gaussian function, giving a diffraction pattern with no secondary rings.:
Two slits
The pattern which occurs when light diffracted from two slits overlaps is of considerable interest in physics, firstly for its importance in establishing the wave theory of light through Young's interference experimentYoung's interference experiment
Young's interference experiment, also called Young's double-slit interferometer, was the original version of the modern double-slit experiment, performed at the beginning of the nineteenth century by Thomas Young. This experiment played a major role in the general acceptance of the wave theory of...
, and secondly because of its role as a thought experiment in Double-slit experiment
Double-slit experiment
The double-slit experiment, sometimes called Young's experiment, is a demonstration that matter and energy can display characteristics of both waves and particles...
in quantum mechanics.
Narrow slits

Solution by integration
The incident light is diffracted by the slits into uniform spherical waves. The waves travelling in a given direction from the two slits have differing phases. The phase of the waves from the upper and lower slits relative to the origin is given by andThe complex amplitude of the summed waves is given by:
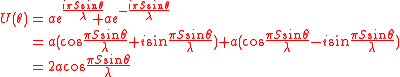
Solution using Fourier transform
The aperture can be represented by the function:
where is the delta function.
We have

and
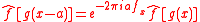
giving
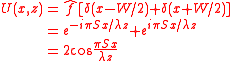
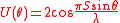
This is the same expression as that derived above by integration.
Intensity
This gives the intensity of the combined waves as: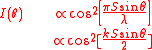
Slits of finite width
The width of the slits, is finite.Solution by integration
The diffracted pattern is given by: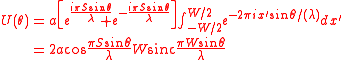
Solution using Fourier transform
The aperture function is given by: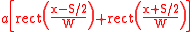
The Fourier transform of this function is given by
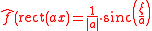
where is the Fourier transform frequency, and the function is here defined as sin(πx)/(πx)
and
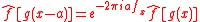
We have
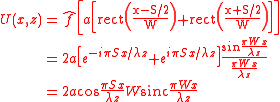
or
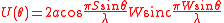
This is the same expression as was derived by integration.
Intensity
The intensity is given by: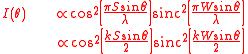
It can be seen that the form of the intensity pattern is the product of the individual slit diffraction pattern, and the interfernce pattern which would be obtained with slits of negligible width. This is illustrated in the image at the right which shows single slit diffraction by a laser beam, and also the diffraction/interference pattern given by two identical slits.
Grating
A grating is defined in Born and Wolf as "any arrangement which imposes on an incident wave a periodic variation of amplitude or phase, or both".Narrow slit grating
A simple grating consists of a screen with N slits whose width is significantly less than the wavelength of the incident light with slit separation of .Solution by integration
The complex amplitude of the diffracted wave at an angle is given by: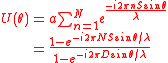
since this is the sum of a geometric series.
Solution using Fourier transform
The aperture is given by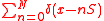
The Fourier transform of this function is:
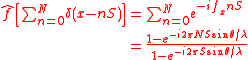
Intensity
The intensity is given by: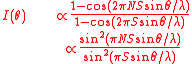
This function has a series of maxima and minima. There are regularly spaced "prinicpal maxima", and a number of much smaller maxima in between the principal maxima. The principal maxima occur when
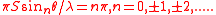
and the main diffracted beams therefore occur at angles:
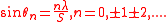
This is the grating equation for normally incident light.
The number of small intermediate maxima is equal to the number of slits, -1 and their size and shape is also determined by .
The form of the pattern for =50 is shown in the first figure .
The detailed structure for 20 and 50 slits gratings are illustrated in the second diagram.
Finite width slit grating
The grating now has N slits of width and spacingSolution using integration
The amplitude is given by: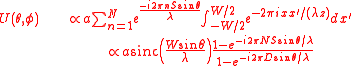
Solution using Fourier transform
The aperture function can be written as:
Using the convolution theorem which says that if we have two functions and , and we have
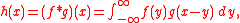
where ∗ denotes the convolution operation, then we also have
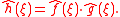
we can write the aperture function as

The amplitude is then given by the Fourier transform of this expression as:
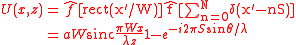
Intensity
The intensity is given by:
The diagram shows the diffraction pattern for a grating with 20 slits, where the width of the slits is 1/5th of the slit separation. The size of the main diffracted peaks is modulated with the diffraction pattern of the individual slits.
Other gratings
The Fourier transform method above can be used to find the form of the diffraction for any periodic structure where the Fourier transform of the structure is known. Goodman uses this method to derive expressions for the diffraction pattern obtained with sinsoidal amplitude and phase modulation gratings. These are of particular interest in holographyHolography
Holography is a technique that allows the light scattered from an object to be recorded and later reconstructed so that when an imaging system is placed in the reconstructed beam, an image of the object will be seen even when the object is no longer present...
.
Non-normal illumination=
If the aperture is illuminated by a mono-chromatic plane wave incident in a direction , the first version of the Fraunhofer equation above becomes:
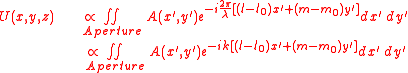
The equations used to model each of the systems above are altered only by changes in the constants multiplying and , so the difffracted light patterns will have the form, except that they will now be centred around the direction of the incident plane wave.
The grating equation becomes
 .
.Non-monochromatic illumination=
In all of the above examples of Fraunhofer diffraction, the effect of increasing the wavelength of the illuminating light is to reduce the size of the diffraction structure, and conversely, when the wavelength is reduced, the size of the pattern increases. If the light is not mono-chromatic, i.e. it consists of a range of different wavelengths, each wavelength is diffracted into a pattern of a slightly different size to its neighbours. If the spread of wavelengths is significantly smaller than the mean wavelength, the individual patterns will vary very little in size, and so the basic diffraction will still appear with slightly reduced contrast. As the spread of wavelengths is increased, the number of "fringes" which can be observed is reduced.
See also =
- Kirchhoff's diffraction formulaKirchhoff's diffraction formulaKirchhoff's diffraction formula can be used to model the propagation of light in a wide range of configurations, either analytically or using numerical modelling. It gives an expression for the wave disturbance when a monochromatic spherical wave passes through an opening in an opaque screen...
- Fresnel diffractionFresnel diffractionIn optics, the Fresnel diffraction equation for near-field diffraction, is an approximation of Kirchhoff-Fresnel diffraction that can be applied to the propagation of waves in the near field....
- Huygens Principle
- Airy discAiry discIn optics, the Airy disk and Airy pattern are descriptions of the best focused spot of light that a perfect lens with a circular aperture can make, limited by the diffraction of light....
- Fourier opticsFourier opticsFourier optics is the study of classical optics using Fourier transforms and can be seen as the dual of the Huygens-Fresnel principle. In the latter case, the wave is regarded as a superposition of expanding spherical waves which radiate outward from actual current sources via a Green's function...
Reference sources=
- Abramowitz Milton & Segun Irene A.,1964, Dover Publications Inc, New York.
- Born MMax BornMax Born was a German-born physicist and mathematician who was instrumental in the development of quantum mechanics. He also made contributions to solid-state physics and optics and supervised the work of a number of notable physicists in the 1920s and 30s...
& Wolf E, Principles of Optics, 1999, 7th Edition, Cambridge University Press, ISBN 13 978-0-521-64222-4 - Goodman Joseph, 2005, Introduction to Fourier Optics, Roberts & Co. ISBN 0974707724 or online here
- Heavens OS and Ditchburn W, 1991, Insight into Optics, Longman and Sons, Chichester ISBN 978-0471927693
- Hecht Eugene, Optics, 2002, Addison Wesley, ISBN-0-321-18878-0
- Jenkins FA & White HE, 1957, Fundamentals of Optics, 3rd Edition, McGraw Hill, New York
- Lipson A., Lipson SG, Lipson HHenry LipsonHenry Lipson CBE was a British physicist. He was Professor of Physics, University of Manchester Institute of Science and Technology, 1954-77, then Professor Emeritus....
, 2011, Optical Physics, Cambridge University Press, ISBN=978-0-521-40345-1 - Longhurst RS, 1967, Geometrical and Physical Optics, 2nd Edition, Longmans, London
- Whittaker and Watson, 1962, Modern Analysis, Cambridge University Press.

