
Airy disc
Encyclopedia

Optics
Optics is the branch of physics which involves the behavior and properties of light, including its interactions with matter and the construction of instruments that use or detect it. Optics usually describes the behavior of visible, ultraviolet, and infrared light...
, the Airy disk (or Airy disc) and Airy pattern are descriptions of the best focused spot of light that a perfect lens
Lens (optics)
A lens is an optical device with perfect or approximate axial symmetry which transmits and refracts light, converging or diverging the beam. A simple lens consists of a single optical element...
with a circular aperture
Aperture
In optics, an aperture is a hole or an opening through which light travels. More specifically, the aperture of an optical system is the opening that determines the cone angle of a bundle of rays that come to a focus in the image plane. The aperture determines how collimated the admitted rays are,...
can make, limited by the diffraction
Diffraction
Diffraction refers to various phenomena which occur when a wave encounters an obstacle. Italian scientist Francesco Maria Grimaldi coined the word "diffraction" and was the first to record accurate observations of the phenomenon in 1665...
of light
Light
Light or visible light is electromagnetic radiation that is visible to the human eye, and is responsible for the sense of sight. Visible light has wavelength in a range from about 380 nanometres to about 740 nm, with a frequency range of about 405 THz to 790 THz...
.
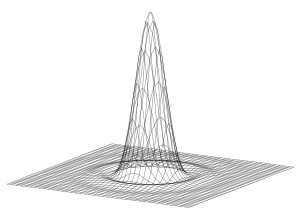
The diffraction pattern resulting from a uniformly-illuminated circular aperture has a bright region in the center, known as the Airy disk which together with the series of concentric bright rings around is called the Airy pattern. Both are named after George Biddell Airy
George Biddell Airy
Sir George Biddell Airy PRS KCB was an English mathematician and astronomer, Astronomer Royal from 1835 to 1881...
. The disk and rings phenomenon had been known prior to Airy; John Herschel
John Herschel
Sir John Frederick William Herschel, 1st Baronet KH, FRS ,was an English mathematician, astronomer, chemist, and experimental photographer/inventor, who in some years also did valuable botanical work...
described the appearance of a bright star seen through a telescope under high magnification for an 1828 article on light for the Encyclopedia Metropolitana:
...the star is then seen (in favourable circumstances of tranquil atmosphere, uniform temperature, &c.) as a perfectly round, well-defined planetary disc, surrounded by two, three, or more alternately dark and bright rings, which, if examined attentively, are seen to be slightly coloured at their borders. They succeed each other nearly at equal intervals round the central disc....
However, Airy wrote the first full theoretical treatment explaining the phenomenon (his 1835 "On the Diffraction of an Object-glass with Circular Aperture").
Mathematically, the diffraction pattern is characterized by the wavelength of light illuminating the circular aperture, and the aperture's size. The appearance of the diffraction pattern is additionally characterized by the sensitivity of the eye or other detector used to observe the pattern.
The most important application of this concept is in cameras and telescopes. Owing to diffraction, the smallest point to which a lens or mirror can focus a beam of light is the size of the Airy disk. Even if one were able to make a perfect lens, there is still a limit to the resolution of an image created by this lens. An optical system in which the resolution is no longer limited by imperfections in the lenses but only by diffraction is said to be diffraction limited.
The Airy disk is of importance in physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, optics
Optics
Optics is the branch of physics which involves the behavior and properties of light, including its interactions with matter and the construction of instruments that use or detect it. Optics usually describes the behavior of visible, ultraviolet, and infrared light...
, and astronomy
Astronomy
Astronomy is a natural science that deals with the study of celestial objects and phenomena that originate outside the atmosphere of Earth...
.
Size
Far away from the aperture, the angle at which the first minimum occurs, measured from the direction of incoming light, is given by the approximate formula: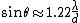
or, for small angles, simply
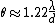
where θ is in radians and λ is the wavelength of the light and d is the diameter of the aperture. Airy wrote this as

where s was the angle of first minimum in seconds of arc, a was the radius of the aperture in inches, and the wavelength of light was assumed to be 0.000022 inches (the mean of visible wavelengths). The Rayleigh criterion
Angular resolution
Angular resolution, or spatial resolution, describes the ability of any image-forming device such as an optical or radio telescope, a microscope, a camera, or an eye, to distinguish small details of an object...
for barely resolving two objects that are point sources of light, such as stars seen through a telescope, is that the center of the Airy disk for the first object occurs at the first minimum of the Airy disk of the second. This means that the angular resolution of a diffraction limited system is given by the same formulae.
However, while the angle at which the first minimum occurs (which is sometimes described as the radius of the Airy disk) depends only on wavelength and aperture size, the appearance of the diffraction pattern will vary with the intensity (brightness) of the light source. Because any detector (eye, film, digital) used to observe the diffraction pattern can have an intensity threshold for detection, the full diffraction pattern may not be apparent. In astronomy, the outer rings are frequently not apparent even in a highly magnified image of a star. It may be that none of the rings are apparent, in which case the star image appears as a disk (central maximum only) rather than as a full diffraction pattern. Furthermore, fainter stars will appear as smaller disks than brighter stars, because less of their central maximum reaches the threshold of detection. While in theory all stars or other "point sources" of a given wavelength and seen through a given aperture have the same Airy disk radius characterized by the above equation (and the same size diffraction pattern), differing only in intensity (the "height" of the surface plot at upper right), the appearance is that fainter sources appear as smaller disks, and brighter sources appear as larger disks. This was described by Airy in his original work:
The rapid decrease of light in the successive rings will sufficiently explain the visibility of two or three rings with a very bright star and the non-visibility of rings with a faint star. The difference of the diameters of the central spots (or spurious disks) of different stars ... is also fully explained. Thus the radius of the spurious disk of a faint star, where light of less than half the intensity of the central light makes no impression on the eye, is determined by [s = 1.17/a], whereas the radius of the spurious disk of a bright star, where light of 1/10 the intensity of the central light is sensible, is determined by [s=1.97/a].).
Despite this feature of Airy's work, the radius of the Airy disk is often given as being simply the angle of first minimum, even in standard textbooks. In reality, the angle of first minimum is a limiting value for the size of the Airy disk, and not a definite radius.
Cameras
If two objects imaged by a camera are separated by an angle small enough that their Airy disks on the camera detector start overlapping, the objects can not be clearly separated any more in the image, and they start blurring together. Two objects are said to be just resolved when the maximum of the first Airy pattern falls on top of the first minimum of the second Airy pattern (the Rayleigh criterion).Therefore the smallest angular separation two objects can have before they significantly blur together is given as stated above by
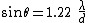
Thus, the ability of the system to resolve detail is limited by the ratio of λ/d. The larger the aperture for a given wavelength, the finer the detail which can be distinguished in the image.
Since θ is small we can approximate this by

where
 is the separation of the images of the two objects on the film and
is the separation of the images of the two objects on the film and 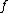 is the distance from the lens to the film.
is the distance from the lens to the film.If we take the distance from the lens to the film to be approximately equal to the focal length
Focal length
The focal length of an optical system is a measure of how strongly the system converges or diverges light. For an optical system in air, it is the distance over which initially collimated rays are brought to a focus...
of the lens, we find
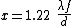
but
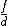 is the f-number
is the f-numberF-number
In optics, the f-number of an optical system expresses the diameter of the entrance pupil in terms of the focal length of the lens; in simpler terms, the f-number is the focal length divided by the "effective" aperture diameter...
of a lens. A typical setting for use on an overcast day would be . For blue visible light, the wavelength λ is about 420 nanometers. This gives a value for
 of about 4 µm. In a digital camera, making the pixels of the image sensor
of about 4 µm. In a digital camera, making the pixels of the image sensorImage sensor
An image sensor is a device that converts an optical image into an electronic signal. It is used mostly in digital cameras and other imaging devices...
smaller than this would not actually increase image resolution
Image resolution
Image resolution is an umbrella term that describes the detail an image holds. The term applies to raster digital images, film images, and other types of images. Higher resolution means more image detail....
.
The human eye

F-number
In optics, the f-number of an optical system expresses the diameter of the entrance pupil in terms of the focal length of the lens; in simpler terms, the f-number is the focal length divided by the "effective" aperture diameter...
for the human eye is about 2.1, corresponding to a diffraction-limited point spread function
Point spread function
The point spread function describes the response of an imaging system to a point source or point object. A more general term for the PSF is a system's impulse response, the PSF being the impulse response of a focused optical system. The PSF in many contexts can be thought of as the extended blob...
with approximately 1 μm diameter. However, at this f-number, spherical aberration limits visual acuity, while a 3 mm pupil diameter (f/5.7) approximates the resolution achieved by the human eye. The maximum density of cones in the human fovea
Fovea
The fovea centralis, also generally known as the fovea , is a part of the eye, located in the center of the macula region of the retina....
is approximately 170,000 per square millimeter, which implies that the cone spacing in the human eye is about 2.5 μm, approximately the diameter of the point spread function at f/5.
Focused laser beam
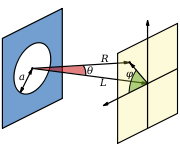
A circular laser beam with uniform intensity across the circle (a flat-top beam) focused by a lens will form an Airy disk pattern at the focus. The size of the Airy disk determines the laser intensity at the focus.Conditions for observation
Light from a uniformly illuminated circular aperture (or from a uniform, flattop beam) will exhibit an Airy diffraction pattern far away from the aperture due to Fraunhofer diffractionFraunhofer diffraction
In optics, the Fraunhofer diffraction equation is used to model the diffraction of waves when the diffraction pattern is viewed at a long distance from the diffracting object, and also when it is viewed at the focal plane of an imaging lens....
(far-field diffraction).
The conditions for being in the far field and exhibiting an Airy pattern are: the incoming light illuminating the aperture is a plane wave (no phase variation across the aperture), the intensity is constant over the area of the aperture, and the distance R from the aperture where the diffracted light is observed (the screen distance) is large compared to the aperture size, and the radius
 of the aperture is not too much larger than the wavelength
of the aperture is not too much larger than the wavelength 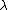 of the light. The last two conditions can be formally written as
of the light. The last two conditions can be formally written as 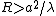 .
.In practice, the conditions for uniform illumination can be met by placing the source of the illumination far from the aperture. If the conditions for far field are not met (for example if the aperture is large), the far-field Airy diffraction pattern can also be obtained on a screen much closer to the aperture by using a lens right after the aperture (or the lens itself can form the aperture). The Airy pattern will then be formed at the focus of the lens rather than at infinity.
Hence, the focal spot of a uniform circular laser beam (a flattop beam) focused by a lens will also be an Airy pattern.
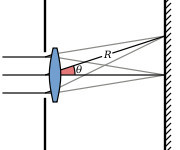
In a camera or imaging system an object far away gets imaged onto the film or detector plane by the objective lens, and the far field diffraction pattern is observed at the detector. The resulting image is a convolution of the ideal image with the Airy diffraction pattern due to diffraction from the iris aperture or due to the finite size of the lens. This leads to the finite resolution of a lens system described above.
Mathematical details
Intensity (physics)
In physics, intensity is a measure of the energy flux, averaged over the period of the wave. The word "intensity" here is not synonymous with "strength", "amplitude", or "level", as it sometimes is in colloquial speech...
of the Fraunhofer diffraction
Fraunhofer diffraction
In optics, the Fraunhofer diffraction equation is used to model the diffraction of waves when the diffraction pattern is viewed at a long distance from the diffracting object, and also when it is viewed at the focal plane of an imaging lens....
pattern of a circular aperture (the Airy pattern) is given by the squared modulus of the Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
of the circular aperture:
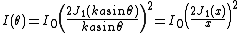
where
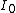 is the maximum intensity of the pattern at the Airy disc center,
is the maximum intensity of the pattern at the Airy disc center,  is the Bessel function
is the Bessel functionBessel function
In mathematics, Bessel functions, first defined by the mathematician Daniel Bernoulli and generalized by Friedrich Bessel, are canonical solutions y of Bessel's differential equation:...
of the first kind of order one,
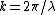 is the wavenumber,
is the wavenumber,  is the radius of the aperture, and
is the radius of the aperture, and  is the angle of observation, i.e. the angle between the axis of the circular aperture and the line between aperture center and observation point.
is the angle of observation, i.e. the angle between the axis of the circular aperture and the line between aperture center and observation point. 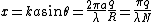 , where q is the radial distance from the optics axis in the observation (or focal) plane and
, where q is the radial distance from the optics axis in the observation (or focal) plane and 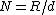 (d=2a is the aperture diameter, R is the observation distance) is the f-number
(d=2a is the aperture diameter, R is the observation distance) is the f-numberF-number
In optics, the f-number of an optical system expresses the diameter of the entrance pupil in terms of the focal length of the lens; in simpler terms, the f-number is the focal length divided by the "effective" aperture diameter...
of the system.
If a lens after the aperture is used, the Airy pattern forms at the focal plane of the lens, where R = f (f is the focal length of the lens).
Note that the limit for
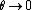 (or for
(or for 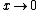 ) is
) is 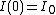 .
.The zeros of
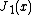 are at
are at 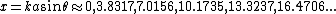 . From this follows that the first dark ring in the diffraction pattern occurs where
. From this follows that the first dark ring in the diffraction pattern occurs where 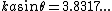 , or
, or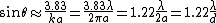 .
.The radius
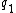 of the first dark ring on a screen is related to
of the first dark ring on a screen is related to 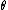 and to the f-number
and to the f-numberF-number
In optics, the f-number of an optical system expresses the diameter of the entrance pupil in terms of the focal length of the lens; in simpler terms, the f-number is the focal length divided by the "effective" aperture diameter...
by

where R is the distance from the aperture, and the f-number
F-number
In optics, the f-number of an optical system expresses the diameter of the entrance pupil in terms of the focal length of the lens; in simpler terms, the f-number is the focal length divided by the "effective" aperture diameter...
N = R/d is the ratio of observation distance to aperture size. The half maximum of the central Airy disk (where
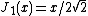 ) occurs at
) occurs at 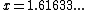 ; the 1/e2 point (where
; the 1/e2 point (where 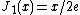 ) occurs at
) occurs at 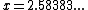 , and the maximum of the first ring occurs at
, and the maximum of the first ring occurs at  .
.The intensity
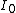 at the center of the diffraction pattern is related to the total power
at the center of the diffraction pattern is related to the total power  incident on the aperture by
incident on the aperture by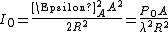
where
 is the source strength per unit area at the aperture, A is the area of the aperture (
is the source strength per unit area at the aperture, A is the area of the aperture (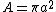 ) and R is the distance from the aperture. At the focal plane of a lens,
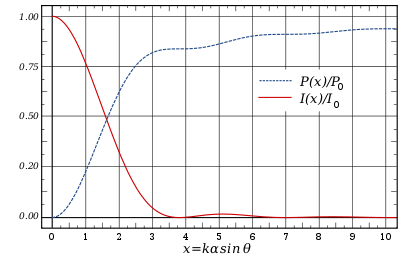
) and R is the distance from the aperture. At the focal plane of a lens, 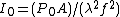 . The intensity at the maximum of the first ring is about 1.75% of the intensity at the center of the Airy disk.
. The intensity at the maximum of the first ring is about 1.75% of the intensity at the center of the Airy disk.The expression for
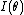 above can be integrated to give the total power contained in the diffraction pattern within a circle of given size:
above can be integrated to give the total power contained in the diffraction pattern within a circle of given size: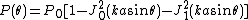
where
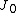 and
and 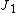 are Bessel function
are Bessel functionBessel function
In mathematics, Bessel functions, first defined by the mathematician Daniel Bernoulli and generalized by Friedrich Bessel, are canonical solutions y of Bessel's differential equation:...
s. Hence the fractions of the total power contained within the first, second, and third dark rings (where
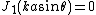 ) are 83.8%, 91.0%, and 93.8% respectively.
) are 83.8%, 91.0%, and 93.8% respectively.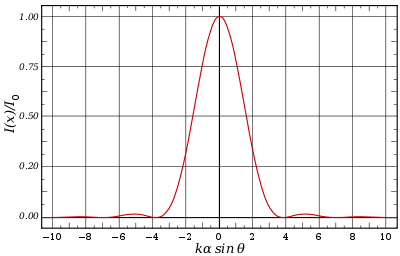 |
 |
Approximation using a Gaussian profile

Root mean square
In mathematics, the root mean square , also known as the quadratic mean, is a statistical measure of the magnitude of a varying quantity. It is especially useful when variates are positive and negative, e.g., sinusoids...
(RMS) spotsize is undefined (i.e. infinite). An alternative measure of the spot size is to ignore the relatively small outer rings of the Airy pattern and to approximate the central lobe with a Gaussian profile, such that
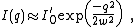
where
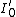 is the irradiance at the center of the pattern,
is the irradiance at the center of the pattern, 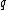 represents the radial distance from the center of the pattern, and
represents the radial distance from the center of the pattern, and 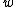 is the Gaussian width. If we equate the peak amplitude of the Airy pattern and Gaussian profile, that is,
is the Gaussian width. If we equate the peak amplitude of the Airy pattern and Gaussian profile, that is,  , and find the value of
, and find the value of 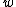 giving the optimal approximation to the pattern, we obtain
giving the optimal approximation to the pattern, we obtain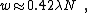
where N is the f-number. If, on the other hand, we wish to enforce that the Gaussian profile has the same volume as does the Airy pattern, then this becomes
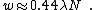
In optical aberration theory, it is common to describe an imaging system as diffraction-limited if the Airy disk radius is larger than the RMS spotsize determined from geometric ray tracing (see Optical lens design
Optical lens design
Optical lens design refers to the calculation of lens construction parameters that will meet a set of performance requirements and constraints, including cost and schedule limitations....
). Since the RMS spotsize is equivalent to the standard deviation
Standard deviation
Standard deviation is a widely used measure of variability or diversity used in statistics and probability theory. It shows how much variation or "dispersion" there is from the average...
of a function, the Gaussian profile approximation provides a convenient means of comparison: here the RMS spotsize is just the Gaussian width parameter,
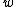 . And, using the approximation above shows that the RMS spotsize of the Gaussian approximation to the Airy disk is about one-third that of the Airy disk radius, i.e.
. And, using the approximation above shows that the RMS spotsize of the Gaussian approximation to the Airy disk is about one-third that of the Airy disk radius, i.e. 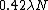 as opposed to
as opposed to 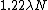 .
.Obscured Airy pattern
Similar equations can also be derived for the obscured Airy diffraction pattern which is the diffraction pattern from an annular aperture or beam, i.e. a uniform circular aperture (beam) obscured by a circular block at the center. This situation is relevant to many common reflector telescope designs that incorporate a secondary mirror, including Newtonian telescopeNewtonian telescope
The Newtonian telescope is a type of reflecting telescope invented by the British scientist Sir Isaac Newton , using a concave primary mirror and a flat diagonal secondary mirror. Newton’s first reflecting telescope was completed in 1668 and is the earliest known functional reflecting telescope...
s and Schmidt–Cassegrain telescopes.
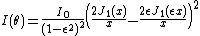
where
 is the annular aperture obscuration ratio, or the ratio of the diameter of the obscuring disk and the diameter of the aperture (beam).
is the annular aperture obscuration ratio, or the ratio of the diameter of the obscuring disk and the diameter of the aperture (beam). 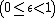 , and x is defined as above:
, and x is defined as above: 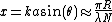 where
where 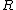 is the radial distance in the focal plane from the optical axis,
is the radial distance in the focal plane from the optical axis, 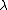 is the wavelength and
is the wavelength and 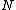 is the f-number
is the f-numberF-number
In optics, the f-number of an optical system expresses the diameter of the entrance pupil in terms of the focal length of the lens; in simpler terms, the f-number is the focal length divided by the "effective" aperture diameter...
of the system. The fractional encircled energy (the fraction of the total energy contained within a circle of radius
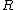 centered at the optical axis in the focal plane) is then given by:
centered at the optical axis in the focal plane) is then given by:
For
 the formulas reduce to the unobscured versions above.
the formulas reduce to the unobscured versions above.Comparison to Gaussian beam focus
A circular laser beam with uniform intensity profile, focused by a lens, will form an Airy pattern at the focal plane of the lens. The intensity at the center of the focus will be where
where  is the total power of the beam,
is the total power of the beam,  is the area of the beam (
is the area of the beam ( is the beam diameter),
is the beam diameter), 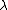 is the wavelength, and
is the wavelength, and  is the focal length of the lens.
is the focal length of the lens.A Gaussian beam with
 diameter of D focused through an aperture of diameter D will have a focal profile that is nearly Gaussian, and the intensity at the center of the focus will be 0.924 times
diameter of D focused through an aperture of diameter D will have a focal profile that is nearly Gaussian, and the intensity at the center of the focus will be 0.924 times 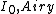 .
.See also
- Fraunhofer diffractionFraunhofer diffractionIn optics, the Fraunhofer diffraction equation is used to model the diffraction of waves when the diffraction pattern is viewed at a long distance from the diffracting object, and also when it is viewed at the focal plane of an imaging lens....
- Amateur astronomyAmateur astronomyAmateur astronomy, also called backyard astronomy and stargazing, is a hobby whose participants enjoy watching the night sky , and the plethora of objects found in it, mainly with portable telescopes and binoculars...
- Point spread functionPoint spread functionThe point spread function describes the response of an imaging system to a point source or point object. A more general term for the PSF is a system's impulse response, the PSF being the impulse response of a focused optical system. The PSF in many contexts can be thought of as the extended blob...
- Optical unitOptical unitThe Optical Unit is a dimensionless units of length used in optical microscopy. Because every diffraction limited system have their resolution proportional to wavelength / NA, it is convenient for comparison to use this unit....
External links
- "Concepts and Formulas in Microscopy: Resolution" by Michael W. Davidson, Nikon MicroscopyU (website).
- "Image Formation: Numerical Aperture and Image Resolution" (Interactive Java Tutorial) by Kenneth R. Spring, Brian O. Flynn, and Michael W. Davidson, Molecular Expressions (website), June 15, 2006.
- "Image Formation: Airy Pattern Formation" (Interactive Java Tutorial) by Kenneth R. Spring, Brian O. Flynn, and Michael W. Davidson, Molecular Expressions (website), June 15, 2006.
- "Diffraction from a Circular Aperture" by Paul Padley, Connexions (website), November 8, 2005. – Mathematical details to derive the above formula.
- "The Airy Disk: An Explanation Of What It Is, And Why You Can’t Avoid It", Oldham Optical UK.

