
Fitting subgroup
Encyclopedia
In mathematics
, especially in the area of algebra
known as group theory
, the Fitting subgroup F of a finite
group
G, named after Hans Fitting
, is the unique largest normal
nilpotent
subgroup
of G. Intuitively, it represents the smallest subgroup which "controls" the structure of G when G is solvable
. When G is not solvable, a similar role is played by the generalized Fitting subgroup F*, which is generated by the Fitting subgroup and the components
of G.
For an arbitrary (not necessarily finite) group G, the Fitting subgroup is defined to be the subgroup generated by the nilpotent normal subgroups of G. For infinite groups, the Fitting subgroup is not always nilpotent.
The remainder of this article deals exclusively with finite group
s.
of the Fitting subgroup of a finite group is guaranteed by Fitting's theorem
which says that the product of a finite collection of normal nilpotent subgroups of G is again a normal nilpotent subgroup. It may also be explicitly constructed as the product of the p-cores
of G over all of the primes p dividing the order of G.
If G is a finite non-trivial solvable group then the Fitting subgroup is always non-trivial, i.e. if G≠1 is finite solvable, then F(G)≠1. Similarly the Fitting subgroup of G/F(G) will be nontrivial if G is not itself nilpotent, giving rise to the concept of Fitting length
. Since the Fitting subgroup of a finite solvable group contains its own centralizer, this gives a method of understanding finite solvable groups as extensions
of nilpotent groups by faithful automorphism groups of nilpotent groups.
In a nilpotent group, every chief factor is centralized by every element. Relaxing the condition somewhat, and taking the subgroup of elements of a general finite group which centralize every chief factor, one simply gets the Fitting subgroup again :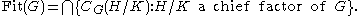
The generalization to p-nilpotent groups is similar.
quasisimple
subgroup. (A group is quasisimple if it is a perfect
central extension of a simple group.) The layer E(G) or L(G) of a group is the subgroup generated by all components. Any two components of a group commute, so the layer is a perfect central extension of a product of simple groups, and is the largest normal subgroup of G with this structure. The generalized Fitting subgroup F*(G) is the subgroup generated by the layer and the Fitting subgroup. The layer commutes with the Fitting subgroup, so the generalized Fitting subgroup is a central extension of a product of p-groups and simple group
s.
The layer is also the maximal normal semisimple subgroup, where a group is called semisimple if it is a perfect central extension of a product of simple groups.
The definition of the generalized Fitting subgroup looks a little strange at first. To motivate it, consider the problem of trying to find a normal subgroup H of G that contains its own centralizer and the Fitting group. If C is the centralizer of H we want to prove that C is contained in H. If not, pick a minimal characteristic subgroup
M/Z(H) of C/Z(H), where Z(H) is the center of H, which is the same as the intersection of C and H. Then M/Z(H) is a product of simple or cyclic group
s as it is characteristically simple. If M/Z(H) is a product of cyclic groups then M must be in the Fitting subgroup. If M/Z(H) is a product of non-abelian simple groups then the derived subgroup of M is a normal semisimple subgroup mapping onto M/Z(H). So if H contains the Fitting subgroup and all normal semisimple subgroups, then M/Z(H) must be trivial, so H contains its own centralizer. The generalized Fitting subgroup is the smallest subgroup that contains the Fitting subgroup and all normal semisimple subgroups.
The generalized Fitting subgroup can also be viewed as a generalized centralizer of chief factors. A nonabelian semisimple group cannot centralize itself, but it does act one itself as inner automorphisms. A group is said to be quasi-nilpotent if every element acts as an inner automorphism on every chief factor. The generalized Fitting subgroup is the unique largest subnormal quasi-nilpotent subgroup, and is equal to the set of all elements which act as inner automorphisms on every chief factor of the whole group :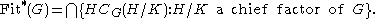
Here an element g is in HCG(H/K) if and only if there is some h in H such that for every x in H, xg ≡ xh mod K.
). A finite group is said to be of characteristic p type if F*(G) is a p-group for every p-local subgroup, because any group of Lie type
defined over a field of characteristic p has this property. In the classification of finite simple groups
, this allows one to guess over which field a simple group should be defined. Note that a few groups are of characteristic p type for more than one p.
If a simple group is not of Lie type over a field of given characteristic p, then the p-local subgroups usually have components in the generalized Fitting subgroup, though there are many exceptions for groups that have small rank, are defined over small fields, or are sporadic. This is used to classify the finite simple groups, because if a p-local subgroup has a known component, it is often possible to identify the whole group .
The analysis of finite simple groups by means of the structure and embedding of the generalized Fitting subgroups of their maximal subgroups was originated by Helmut Bender and has come to be known as Bender's method
. It is especially effective in the exceptional cases where components or signalizer functor
s are not applicable.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, especially in the area of algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
known as group theory
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
, the Fitting subgroup F of a finite
Finite group
In mathematics and abstract algebra, a finite group is a group whose underlying set G has finitely many elements. During the twentieth century, mathematicians investigated certain aspects of the theory of finite groups in great depth, especially the local theory of finite groups, and the theory of...
group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
G, named after Hans Fitting
Hans Fitting
Hans Fitting was a mathematician who worked in group theory...
, is the unique largest normal
Normal subgroup
In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
nilpotent
Nilpotent group
In mathematics, more specifically in the field of group theory, a nilpotent group is a group that is "almost abelian". This idea is motivated by the fact that nilpotent groups are solvable, and for finite nilpotent groups, two elements having relatively prime orders must commute...
subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
of G. Intuitively, it represents the smallest subgroup which "controls" the structure of G when G is solvable
Solvable group
In mathematics, more specifically in the field of group theory, a solvable group is a group that can be constructed from abelian groups using extensions...
. When G is not solvable, a similar role is played by the generalized Fitting subgroup F*, which is generated by the Fitting subgroup and the components
Component (group theory)
In mathematics, in the field of group theory, a component of a finite group is a quasisimple subnormal subgroup. Any two distinct components commute...
of G.
For an arbitrary (not necessarily finite) group G, the Fitting subgroup is defined to be the subgroup generated by the nilpotent normal subgroups of G. For infinite groups, the Fitting subgroup is not always nilpotent.
The remainder of this article deals exclusively with finite group
Finite group
In mathematics and abstract algebra, a finite group is a group whose underlying set G has finitely many elements. During the twentieth century, mathematicians investigated certain aspects of the theory of finite groups in great depth, especially the local theory of finite groups, and the theory of...
s.
The Fitting subgroup
The nilpotencyNilpotent group
In mathematics, more specifically in the field of group theory, a nilpotent group is a group that is "almost abelian". This idea is motivated by the fact that nilpotent groups are solvable, and for finite nilpotent groups, two elements having relatively prime orders must commute...
of the Fitting subgroup of a finite group is guaranteed by Fitting's theorem
Fitting's theorem
Fitting's theorem is a mathematical theorem proved by Hans Fitting. It can be stated as follows:By induction it follows also that the subgroup generated by a finite collection of nilpotent normal subgroups is nilpotent. This can be used to show that the Fitting subgroup of certain types of groups ...
which says that the product of a finite collection of normal nilpotent subgroups of G is again a normal nilpotent subgroup. It may also be explicitly constructed as the product of the p-cores
Core (group)
In group theory, a branch of mathematics, a core is any of certain special normal subgroups of a group. The two most common types are the normal core of a subgroup and the p-core of a group.-Definition:...
of G over all of the primes p dividing the order of G.
If G is a finite non-trivial solvable group then the Fitting subgroup is always non-trivial, i.e. if G≠1 is finite solvable, then F(G)≠1. Similarly the Fitting subgroup of G/F(G) will be nontrivial if G is not itself nilpotent, giving rise to the concept of Fitting length
Fitting length
In mathematics, especially in the area of algebra known as group theory, the Fitting length measures how far a solvable group is from being nilpotent...
. Since the Fitting subgroup of a finite solvable group contains its own centralizer, this gives a method of understanding finite solvable groups as extensions
Group extension
In mathematics, a group extension is a general means of describing a group in terms of a particular normal subgroup and quotient group. If Q and N are two groups, then G is an extension of Q by N if there is a short exact sequence...
of nilpotent groups by faithful automorphism groups of nilpotent groups.
In a nilpotent group, every chief factor is centralized by every element. Relaxing the condition somewhat, and taking the subgroup of elements of a general finite group which centralize every chief factor, one simply gets the Fitting subgroup again :
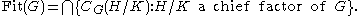
The generalization to p-nilpotent groups is similar.
The generalized Fitting subgroup
A component of a group is a subnormalSubnormal subgroup
In mathematics, in the field of group theory, a subgroup H of a given group G is a subnormal subgroup of G if there is a finite chain of subgroups of the group, each one normal in the next, beginning at H and ending at G....
quasisimple
Quasisimple group
In mathematics, a quasisimple group is a group that is a perfect central extension E of a simple group S...
subgroup. (A group is quasisimple if it is a perfect
Perfect group
In mathematics, more specifically in the area of modern algebra known as group theory, a group is said to be perfect if it equals its own commutator subgroup, or equivalently, if the group has no nontrivial abelian quotients...
central extension of a simple group.) The layer E(G) or L(G) of a group is the subgroup generated by all components. Any two components of a group commute, so the layer is a perfect central extension of a product of simple groups, and is the largest normal subgroup of G with this structure. The generalized Fitting subgroup F*(G) is the subgroup generated by the layer and the Fitting subgroup. The layer commutes with the Fitting subgroup, so the generalized Fitting subgroup is a central extension of a product of p-groups and simple group
Simple group
In mathematics, a simple group is a nontrivial group whose only normal subgroups are the trivial group and the group itself. A group that is not simple can be broken into two smaller groups, a normal subgroup and the quotient group, and the process can be repeated...
s.
The layer is also the maximal normal semisimple subgroup, where a group is called semisimple if it is a perfect central extension of a product of simple groups.
The definition of the generalized Fitting subgroup looks a little strange at first. To motivate it, consider the problem of trying to find a normal subgroup H of G that contains its own centralizer and the Fitting group. If C is the centralizer of H we want to prove that C is contained in H. If not, pick a minimal characteristic subgroup
Characteristic subgroup
In mathematics, particularly in the area of abstract algebra known as group theory, a characteristic subgroup is a subgroup that is invariant under all automorphisms of the parent group. Because conjugation is an automorphism, every characteristic subgroup is normal, though not every normal...
M/Z(H) of C/Z(H), where Z(H) is the center of H, which is the same as the intersection of C and H. Then M/Z(H) is a product of simple or cyclic group
Cyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
s as it is characteristically simple. If M/Z(H) is a product of cyclic groups then M must be in the Fitting subgroup. If M/Z(H) is a product of non-abelian simple groups then the derived subgroup of M is a normal semisimple subgroup mapping onto M/Z(H). So if H contains the Fitting subgroup and all normal semisimple subgroups, then M/Z(H) must be trivial, so H contains its own centralizer. The generalized Fitting subgroup is the smallest subgroup that contains the Fitting subgroup and all normal semisimple subgroups.
The generalized Fitting subgroup can also be viewed as a generalized centralizer of chief factors. A nonabelian semisimple group cannot centralize itself, but it does act one itself as inner automorphisms. A group is said to be quasi-nilpotent if every element acts as an inner automorphism on every chief factor. The generalized Fitting subgroup is the unique largest subnormal quasi-nilpotent subgroup, and is equal to the set of all elements which act as inner automorphisms on every chief factor of the whole group :
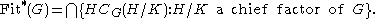
Here an element g is in HCG(H/K) if and only if there is some h in H such that for every x in H, xg ≡ xh mod K.
Properties
If G is a finite solvable group, then the Fitting subgroup contains its own centralizer. The centralizer of the Fitting subgroup is the center of the Fitting subgroup. In this case, the generalized Fitting subgroup is equal to the Fitting subgroup. More generally, if G is any finite group, the generalized Fitting subgroup contains its own centralizer. This means that in some sense the generalized Fitting subgroup controls G, because G modulo the centralizer of F*(G) is contained in the automorphism group of F*(G), and the centralizer of F*(G) is contained in F*(G). In particular there are only a finite number of groups with given generalized Fitting subgroup.Applications
The normalizers of nontrivial p-subgroups of a finite group are called the p-local subgroups and exert a great deal of control over the structure of the group (allowing what is called local analysisLocal analysis
In mathematics, the term local analysis has at least two meanings - both derived from the idea of looking at a problem relative to each prime number p first, and then later trying to integrate the information gained at each prime into a 'global' picture...
). A finite group is said to be of characteristic p type if F*(G) is a p-group for every p-local subgroup, because any group of Lie type
Group of Lie type
In mathematics, a group of Lie type G is a group of rational points of a reductive linear algebraic group G with values in the field k. Finite groups of Lie type form the bulk of nonabelian finite simple groups...
defined over a field of characteristic p has this property. In the classification of finite simple groups
Classification of finite simple groups
In mathematics, the classification of the finite simple groups is a theorem stating that every finite simple group belongs to one of four categories described below. These groups can be seen as the basic building blocks of all finite groups, in much the same way as the prime numbers are the basic...
, this allows one to guess over which field a simple group should be defined. Note that a few groups are of characteristic p type for more than one p.
If a simple group is not of Lie type over a field of given characteristic p, then the p-local subgroups usually have components in the generalized Fitting subgroup, though there are many exceptions for groups that have small rank, are defined over small fields, or are sporadic. This is used to classify the finite simple groups, because if a p-local subgroup has a known component, it is often possible to identify the whole group .
The analysis of finite simple groups by means of the structure and embedding of the generalized Fitting subgroups of their maximal subgroups was originated by Helmut Bender and has come to be known as Bender's method
Bender's method
In group theory, Bender's method is a method introduced by for simplifying the local group theoretic analysis of the odd order theorem. Shortly afterwards he used it to simplify Walter's analysis of groups with abelian Sylow 2-subgroups , and Gorenstein and Walter's classification of groups with...
. It is especially effective in the exceptional cases where components or signalizer functor
Signalizer functor
In mathematics, a signalizer functor gives the intersections of a potential subgroup of a finite group with the centralizers of nontrivial elements of an abelian group. The signalizer functor theorem gives conditions under which a signalizer functor comes from a subgroup...
s are not applicable.

