
Signalizer functor
Encyclopedia
In mathematics, a signalizer functor gives the intersections of a potential subgroup of a finite group with the centralizers of nontrivial elements of an abelian group. The signalizer functor theorem gives conditions under which a signalizer functor comes from a subgroup. The idea is to try and construct a 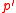 -subgroup of a finite group
-subgroup of a finite group  , which has a good chance of being normal in
, which has a good chance of being normal in  , by taking as generators certain
, by taking as generators certain 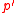 -subgroups of the centralizers of nonidentity elements in one or several given elementary abelian
-subgroups of the centralizers of nonidentity elements in one or several given elementary abelian 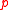 -subgroups of
-subgroups of  The technique has origins in the Feit–Thompson theorem
The technique has origins in the Feit–Thompson theorem
, and was subsequently developed by many people including who defined signalizer functors, who proved the Signalizer Functor Theorem for solvable groups, and who proved it for all groups. This theorem is needed to prove the so-called "dichotomy" stating that a given nonabelian finite simple group
either has local characteristic two, or is of component type. It thus plays a major role in the classification of finite simple groups
.
 be an elementary abelian
be an elementary abelian 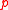 -subgroup of the finite group
-subgroup of the finite group  An A-signalizer functor on
An A-signalizer functor on  or simply a signalizer functor when
or simply a signalizer functor when  and
and  are clear is a mapping
are clear is a mapping  from the set of nonidentity elements of
from the set of nonidentity elements of  to the set of
to the set of  -invariant
-invariant 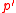 -subgroups of
-subgroups of  satisfying the following properties:
satisfying the following properties:
The second condition above is called the balance condition. If the subgroups are all solvable
are all solvable
, then the signalizer functor itself is said to be solvable.
itself is said to be solvable.
 certain additional, relatively mild, assumptions allow one to prove that the subgroup
certain additional, relatively mild, assumptions allow one to prove that the subgroup 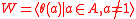 of
of  generated by the subgroups
generated by the subgroups 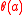 is in fact a
is in fact a  -subgroup. The Solvable Signalizer Functor Theorem proved by Glauberman and mentioned above says that this will be the case if
-subgroup. The Solvable Signalizer Functor Theorem proved by Glauberman and mentioned above says that this will be the case if  is solvable and
is solvable and  has at least three generators. The theorem also states that under these assumptions,
has at least three generators. The theorem also states that under these assumptions,  itself will be solvable.
itself will be solvable.
Using the classification of finite simple groups, showed that is a
is a 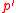 -group without the assumption that
-group without the assumption that  is solvable.
is solvable.
 be a signalizer functor as above, and consider the set И of all
be a signalizer functor as above, and consider the set И of all  -invariant
-invariant 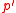 -subgroups
-subgroups  of
of  satisfying the following condition:
satisfying the following condition:
For example, the subgroups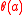 belong to И by the balance condition. The signalizer functor
belong to И by the balance condition. The signalizer functor  is said to be complete if И has a unique maximal element when ordered by containment. In this case, the unique maximal element can be shown to coincide with
is said to be complete if И has a unique maximal element when ordered by containment. In this case, the unique maximal element can be shown to coincide with  above, and
above, and  is called the completion of
is called the completion of  . If
. If  is complete, and
is complete, and  turns out to be solvable, then
turns out to be solvable, then  is said to be solvably complete.
is said to be solvably complete.
Thus, the Solvable Signalizer Functor Theorem can be rephrased by saying that if has at least three generators, then every solvable
has at least three generators, then every solvable  -signalizer functor on
-signalizer functor on  is solvably complete.
is solvably complete.
 -invariant
-invariant 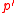 -subgroup
-subgroup 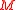 of
of  and define
and define 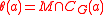 for all nonidentity
for all nonidentity  In practice, however, one begins with
In practice, however, one begins with  and uses it to construct the
and uses it to construct the  -invariant
-invariant 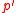 -group.
-group.
The simplest signalizer functor used in practice is this:
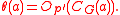
A few words of caution are needed here. First, note that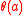 as defined above is indeed an
as defined above is indeed an  -invariant
-invariant 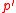 -subgroup of
-subgroup of  because
because  is abelian. However, some additional assumptions are needed to show that this
is abelian. However, some additional assumptions are needed to show that this  satisfies the balance condition. One sufficient criterion is that for each nonidentity
satisfies the balance condition. One sufficient criterion is that for each nonidentity 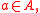 the group
the group 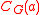 is solvable (or
is solvable (or 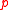 -solvable or even
-solvable or even 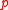 -constrained). Verifying the balance condition for this
-constrained). Verifying the balance condition for this  under this assumption requires a famous lemma, known as Thompson's
under this assumption requires a famous lemma, known as Thompson's
 -lemma. (Note, this lemma is also called Thompson's
-lemma. (Note, this lemma is also called Thompson's  -lemma, but the
-lemma, but the  in this use must not be confused with the
in this use must not be confused with the  appearing in the definition of a signalizer functor!)
appearing in the definition of a signalizer functor!)
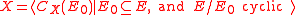
To prove this fact, one uses the Schur–Zassenhaus theorem
to show that for each prime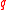 dividing the order of
dividing the order of 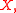 the group
the group  has an
has an  -invariant Sylow
-invariant Sylow 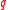 -subgroup. This reduces to the case where
-subgroup. This reduces to the case where  is a
is a 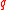 -group. Then an argument by induction on the order of
-group. Then an argument by induction on the order of  reduces the statement further to the case where
reduces the statement further to the case where  is elementary abelian with
is elementary abelian with  acting irreducibly. This forces the group
acting irreducibly. This forces the group 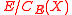 to be cyclic, and the result follows. See either of the books quoted below for details.
to be cyclic, and the result follows. See either of the books quoted below for details.
This is used in both the proof and applications of the Solvable Signalizer Functor Theorem. To begin, notice that it quickly implies the claim that if is complete, then its completion is the group
is complete, then its completion is the group  defined above.
defined above.
 according to the top of the article. Here, the coprime action fact will be used to motivate this claim. Let
according to the top of the article. Here, the coprime action fact will be used to motivate this claim. Let  be a complete
be a complete  -signalizer functor on
-signalizer functor on 
Let be a noncyclic subgroup of
be a noncyclic subgroup of 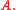 Then the coprime action fact together with the balance condition imply that
Then the coprime action fact together with the balance condition imply that
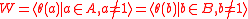 .
.
To see this, observe that because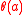 is B-invariant, we have
is B-invariant, we have
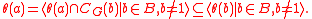
The equality above uses the coprime action fact, and the containment uses the balance condition. Now, it is often the case that satisfies an "equivariance" condition, namely that for each
satisfies an "equivariance" condition, namely that for each  and nonidentity
and nonidentity 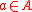

The superscript denotes conjugation by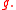 For example, the mapping
For example, the mapping 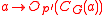 (which is often a signalizer functor!) satisfies this condition. If
(which is often a signalizer functor!) satisfies this condition. If  satisfies equivariance, then the normalizer of
satisfies equivariance, then the normalizer of  will normalize
will normalize  It follows that if
It follows that if  is generated by the normalizers of the noncyclic subgroups of
is generated by the normalizers of the noncyclic subgroups of 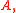 then the completion of
then the completion of  (i.e. W) is normal in
(i.e. W) is normal in 
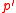 -subgroup of a finite group
-subgroup of a finite group  , which has a good chance of being normal in
, which has a good chance of being normal in  , by taking as generators certain
, by taking as generators certain 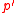 -subgroups of the centralizers of nonidentity elements in one or several given elementary abelian
-subgroups of the centralizers of nonidentity elements in one or several given elementary abelian 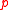 -subgroups of
-subgroups of  The technique has origins in the Feit–Thompson theorem
The technique has origins in the Feit–Thompson theoremFeit–Thompson theorem
In mathematics, the Feit–Thompson theorem, or odd order theorem, states that every finite group of odd order is solvable. It was proved by - History : conjectured that every nonabelian finite simple group has even order...
, and was subsequently developed by many people including who defined signalizer functors, who proved the Signalizer Functor Theorem for solvable groups, and who proved it for all groups. This theorem is needed to prove the so-called "dichotomy" stating that a given nonabelian finite simple group
Simple group
In mathematics, a simple group is a nontrivial group whose only normal subgroups are the trivial group and the group itself. A group that is not simple can be broken into two smaller groups, a normal subgroup and the quotient group, and the process can be repeated...
either has local characteristic two, or is of component type. It thus plays a major role in the classification of finite simple groups
Classification of finite simple groups
In mathematics, the classification of the finite simple groups is a theorem stating that every finite simple group belongs to one of four categories described below. These groups can be seen as the basic building blocks of all finite groups, in much the same way as the prime numbers are the basic...
.
Definition
Let be an elementary abelian
be an elementary abelian 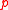 -subgroup of the finite group
-subgroup of the finite group  An A-signalizer functor on
An A-signalizer functor on  or simply a signalizer functor when
or simply a signalizer functor when  and
and  are clear is a mapping
are clear is a mapping  from the set of nonidentity elements of
from the set of nonidentity elements of  to the set of
to the set of  -invariant
-invariant 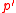 -subgroups of
-subgroups of  satisfying the following properties:
satisfying the following properties:
- For every nonidentity
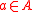 , the group
, the group 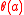 is contained in
is contained in 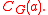
- For every nonidentity
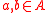 , we have
, we have 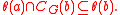
The second condition above is called the balance condition. If the subgroups
 are all solvable
are all solvableSolvable group
In mathematics, more specifically in the field of group theory, a solvable group is a group that can be constructed from abelian groups using extensions...
, then the signalizer functor
 itself is said to be solvable.
itself is said to be solvable.Solvable signalizer functor theorem
Given certain additional, relatively mild, assumptions allow one to prove that the subgroup
certain additional, relatively mild, assumptions allow one to prove that the subgroup 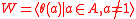 of
of  generated by the subgroups
generated by the subgroups 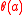 is in fact a
is in fact a  -subgroup. The Solvable Signalizer Functor Theorem proved by Glauberman and mentioned above says that this will be the case if
-subgroup. The Solvable Signalizer Functor Theorem proved by Glauberman and mentioned above says that this will be the case if  is solvable and
is solvable and  has at least three generators. The theorem also states that under these assumptions,
has at least three generators. The theorem also states that under these assumptions,  itself will be solvable.
itself will be solvable.Using the classification of finite simple groups, showed that
 is a
is a 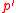 -group without the assumption that
-group without the assumption that  is solvable.
is solvable.Completeness
The terminology of completeness is often used in discussions of signalizer functors. Let be a signalizer functor as above, and consider the set И of all
be a signalizer functor as above, and consider the set И of all  -invariant
-invariant 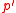 -subgroups
-subgroups  of
of  satisfying the following condition:
satisfying the following condition:
 for all nonidentity
for all nonidentity 
For example, the subgroups
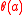 belong to И by the balance condition. The signalizer functor
belong to И by the balance condition. The signalizer functor  is said to be complete if И has a unique maximal element when ordered by containment. In this case, the unique maximal element can be shown to coincide with
is said to be complete if И has a unique maximal element when ordered by containment. In this case, the unique maximal element can be shown to coincide with  above, and
above, and  is called the completion of
is called the completion of  . If
. If  is complete, and
is complete, and  turns out to be solvable, then
turns out to be solvable, then  is said to be solvably complete.
is said to be solvably complete.Thus, the Solvable Signalizer Functor Theorem can be rephrased by saying that if
 has at least three generators, then every solvable
has at least three generators, then every solvable  -signalizer functor on
-signalizer functor on  is solvably complete.
is solvably complete.Examples of signalizer functors
The easiest way to obtain a signalizer functor is to start with an -invariant
-invariant 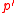 -subgroup
-subgroup 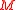 of
of  and define
and define 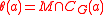 for all nonidentity
for all nonidentity  In practice, however, one begins with
In practice, however, one begins with  and uses it to construct the
and uses it to construct the  -invariant
-invariant 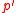 -group.
-group.The simplest signalizer functor used in practice is this:
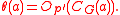
A few words of caution are needed here. First, note that
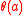 as defined above is indeed an
as defined above is indeed an  -invariant
-invariant 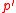 -subgroup of
-subgroup of  because
because  is abelian. However, some additional assumptions are needed to show that this
is abelian. However, some additional assumptions are needed to show that this  satisfies the balance condition. One sufficient criterion is that for each nonidentity
satisfies the balance condition. One sufficient criterion is that for each nonidentity 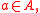 the group
the group 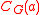 is solvable (or
is solvable (or 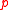 -solvable or even
-solvable or even 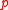 -constrained). Verifying the balance condition for this
-constrained). Verifying the balance condition for this  under this assumption requires a famous lemma, known as Thompson's
under this assumption requires a famous lemma, known as Thompson'sJohn G. Thompson
John Griggs Thompson is a mathematician at the University of Florida noted for his work in the field of finite groups. He was awarded the Fields Medal in 1970, the Wolf Prize in 1992 and the 2008 Abel Prize....
 -lemma. (Note, this lemma is also called Thompson's
-lemma. (Note, this lemma is also called Thompson's  -lemma, but the
-lemma, but the  in this use must not be confused with the
in this use must not be confused with the  appearing in the definition of a signalizer functor!)
appearing in the definition of a signalizer functor!)Coprime action
To obtain a better understanding of signalizer functors, it is essential to know the following general fact about finite groups:- Let
 be an abelian noncyclic group acting on the finite group
be an abelian noncyclic group acting on the finite group  Assume that the orders of
Assume that the orders of  and
and  are relatively prime. Then
are relatively prime. Then
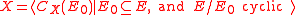
To prove this fact, one uses the Schur–Zassenhaus theorem
Schur–Zassenhaus theorem
The Schur–Zassenhaus theorem is a theorem in group theory which states that if G is a finite group, and N is a normal subgroup whose order is coprime to the order of the quotient group G/N, then G is a semidirect product of N and G/N....
to show that for each prime
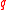 dividing the order of
dividing the order of 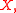 the group
the group  has an
has an  -invariant Sylow
-invariant Sylow 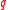 -subgroup. This reduces to the case where
-subgroup. This reduces to the case where  is a
is a 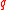 -group. Then an argument by induction on the order of
-group. Then an argument by induction on the order of  reduces the statement further to the case where
reduces the statement further to the case where  is elementary abelian with
is elementary abelian with  acting irreducibly. This forces the group
acting irreducibly. This forces the group 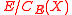 to be cyclic, and the result follows. See either of the books quoted below for details.
to be cyclic, and the result follows. See either of the books quoted below for details.This is used in both the proof and applications of the Solvable Signalizer Functor Theorem. To begin, notice that it quickly implies the claim that if
 is complete, then its completion is the group
is complete, then its completion is the group  defined above.
defined above.Normal completion
The completion of a signalizer functor has a "good chance" of being normal in according to the top of the article. Here, the coprime action fact will be used to motivate this claim. Let
according to the top of the article. Here, the coprime action fact will be used to motivate this claim. Let  be a complete
be a complete  -signalizer functor on
-signalizer functor on 
Let
 be a noncyclic subgroup of
be a noncyclic subgroup of 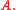 Then the coprime action fact together with the balance condition imply that
Then the coprime action fact together with the balance condition imply that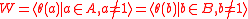 .
.To see this, observe that because
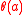 is B-invariant, we have
is B-invariant, we have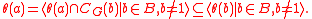
The equality above uses the coprime action fact, and the containment uses the balance condition. Now, it is often the case that
 satisfies an "equivariance" condition, namely that for each
satisfies an "equivariance" condition, namely that for each  and nonidentity
and nonidentity 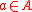

The superscript denotes conjugation by
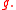 For example, the mapping
For example, the mapping 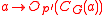 (which is often a signalizer functor!) satisfies this condition. If
(which is often a signalizer functor!) satisfies this condition. If  satisfies equivariance, then the normalizer of
satisfies equivariance, then the normalizer of  will normalize
will normalize  It follows that if
It follows that if  is generated by the normalizers of the noncyclic subgroups of
is generated by the normalizers of the noncyclic subgroups of 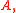 then the completion of
then the completion of  (i.e. W) is normal in
(i.e. W) is normal in 

