Fast inverse square root
Encyclopedia
Hexadecimal
In mathematics and computer science, hexadecimal is a positional numeral system with a radix, or base, of 16. It uses sixteen distinct symbols, most often the symbols 0–9 to represent values zero to nine, and A, B, C, D, E, F to represent values ten to fifteen...
constant 0x5f3759df) is a method of calculating x-½, the reciprocal
Multiplicative inverse
In mathematics, a multiplicative inverse or reciprocal for a number x, denoted by 1/x or x−1, is a number which when multiplied by x yields the multiplicative identity, 1. The multiplicative inverse of a fraction a/b is b/a. For the multiplicative inverse of a real number, divide 1 by the...
(or multiplicative inverse) of a square root
Square root
In mathematics, a square root of a number x is a number r such that r2 = x, or, in other words, a number r whose square is x...
for a 32-bit floating point
Floating point
In computing, floating point describes a method of representing real numbers in a way that can support a wide range of values. Numbers are, in general, represented approximately to a fixed number of significant digits and scaled using an exponent. The base for the scaling is normally 2, 10 or 16...
number in IEEE 754 floating point format. The algorithm was probably developed at Silicon Graphics
Silicon Graphics
Silicon Graphics, Inc. was a manufacturer of high-performance computing solutions, including computer hardware and software, founded in 1981 by Jim Clark...
in the early 1990s, and an implementation appeared in 1999 in the Quake III Arena
Quake III Arena
Quake III Arena , is a multiplayer first-person shooter video game released on December 2, 1999. The game was developed by id Software and featured music composed by Sonic Mayhem and Front Line Assembly...
source code, but the method did not appear on public forums such as Usenet
Usenet
Usenet is a worldwide distributed Internet discussion system. It developed from the general purpose UUCP architecture of the same name.Duke University graduate students Tom Truscott and Jim Ellis conceived the idea in 1979 and it was established in 1980...
until 2002 or 2003. At the time, the primary advantage of the algorithm came from avoiding computationally expensive floating point operations in favor of integer operations. Inverse square roots are used to compute angles of incidence and reflection
Reflection (computer graphics)
Reflection in computer graphics is used to emulate reflective objects like mirrors and shiny surfaces.Reflection is accomplished in a ray trace renderer by following a ray from the eye to the mirror and then calculating where it bounces from, and continuing the process until no surface is found, or...
for lighting
Lighting
Lighting or illumination is the deliberate application of light to achieve some practical or aesthetic effect. Lighting includes the use of both artificial light sources such as lamps and light fixtures, as well as natural illumination by capturing daylight...
and shading
Shading
Shading refers to depicting depth perception in 3D models or illustrations by varying levels of darkness.-Drawing:Shading is a process used in drawing for depicting levels of darkness on paper by applying media more densely or with a darker shade for darker areas, and less densely or with a lighter...
in computer graphics
Computer graphics
Computer graphics are graphics created using computers and, more generally, the representation and manipulation of image data by a computer with help from specialized software and hardware....
.
The algorithm accepts a 32-bit unsigned floating point number as the input and stores a halved value for later use. Then, treating the bits representing the floating point number as a 32-bit integer, a logical shift
Logical shift
In computer science, a logical shift is a bitwise operation that shifts all the bits of its operand. Unlike an arithmetic shift, a logical shift does not preserve a number's sign bit or distinguish a number's exponent from its mantissa; every bit in the operand is simply moved a given number of bit...
right of one bit is performed and the result subtracted from the "magic" value 0x5f3759df. This is the first approximation of the inverse square root of the input. Treating the bits again as floating point it runs one iteration of Newton's method
Newton's method
In numerical analysis, Newton's method , named after Isaac Newton and Joseph Raphson, is a method for finding successively better approximations to the roots of a real-valued function. The algorithm is first in the class of Householder's methods, succeeded by Halley's method...
to return a more precise approximation. This computes an approximation of the inverse square root of a floating point number approximately four times faster than floating point division.
The algorithm was originally attributed to John Carmack, but an investigation showed that the code had deeper roots in both the hardware and software side of computer graphics. Adjustments and alterations passed through both Silicon Graphics and 3dfx Interactive, with Gary Tarolli's implementation for the SGI Indigo
SGI Indigo
The Indigo, introduced as the IRIS Indigo, was a line of workstation computers developed and manufactured by Silicon Graphics, Inc. . The first Indigo, code-named "Hollywood", was introduced on 22 July 1991...
as the earliest known use. It is not known how the constant was originally derived, though investigation has shed some light on possible methods.
Motivation
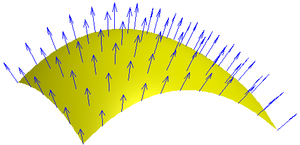
Lambert's cosine law
In optics, Lambert's cosine law says that the radiant intensity observed from a Lambertian surface or a Lambertian radiator is directly proportional to the cosine of the angle θ between the observer's line of sight and the surface normal. A Lambertian surface is also known as an ideal diffusely...
, millions of these calculations must be done per second. Before the creation of specialized hardware to handle transform and lighting, software computations could be slow. Specifically, when the code was developed in the early 1990s, most floating point processing power lagged behind the speed of integer processing.
To normalize a vector, the length of the vector is determined by calculating its Euclidean norm: the square root of the sum of squares of the vector components. When each component of the vector is divided by that length, the new vector will be a unit vector pointing in the same direction.
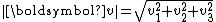is the Euclidean norm of the vector, analogous to the calculation of the Euclidean distanceEuclidean distance
In mathematics, the Euclidean distance or Euclidean metric is the "ordinary" distance between two points that one would measure with a ruler, and is given by the Pythagorean formula. By using this formula as distance, Euclidean space becomes a metric space...
between two points in Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
.
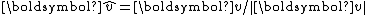is the normalized (unit) vector. Using 
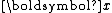to represent 
,
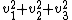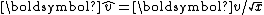, which relates the unit vector to the inverse square root of the distance components.Quake III Arena used the fast inverse square root algorithm to speed graphics processing unit computation, but the algorithm has since been implemented in some dedicated hardware vertex shaders using Field-programmable gate array
Field-programmable gate array
A field-programmable gate array is an integrated circuit designed to be configured by the customer or designer after manufacturing—hence "field-programmable"...
s (FPGA).
Overview of the code
The following code is the fast inverse square root implementation from Quake III ArenaQuake III Arena
Quake III Arena , is a multiplayer first-person shooter video game released on December 2, 1999. The game was developed by id Software and featured music composed by Sonic Mayhem and Front Line Assembly...
, stripped of C preprocessor
C preprocessor
The C preprocessor is the preprocessor for the C and C++ computer programming languages. The preprocessor handles directives for source file inclusion , macro definitions , and conditional inclusion ....
directives, but including the exact original comment text:
float Q_rsqrt( float number )
{
long i;
float x2, y;
const float threehalfs = 1.5F;
x2 = number * 0.5F;
y = number;
i = * ( long * ) &y; // evil floating point bit level hacking
i = 0x5f3759df - ( i >> 1 ); // what the fuck?
y = * ( float * ) &i;
y = y * ( threehalfs - ( x2 * y * y ) ); // 1st iteration
// y = y * ( threehalfs - ( x2 * y * y ) ); // 2nd iteration, this can be removed
return y;
}
In order to determine the inverse square root, an approximation for
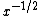would be determined by the software, then some numerical method would revise that approximation until it came within an acceptable error range of the actual result. Common software methodsMethods of computing square roots
There are several methods for calculating the principal square root of a nonnegative real number. For the square roots of a negative or complex number, see below.- Rough estimation :...
in the early 1990s drew a first approximation from a lookup table
Lookup table
In computer science, a lookup table is a data structure, usually an array or associative array, often used to replace a runtime computation with a simpler array indexing operation. The savings in terms of processing time can be significant, since retrieving a value from memory is often faster than...
. This bit of code proved faster than table lookups and approximately four times faster than regular floating point division. Some loss of precision occurred, but was offset by the significant gains in performance. The algorithm was designed with the IEEE 754-2008 32-bit floating point specification in mind, but investigation from Chris Lomont and later Charles McEniry showed that it could be implemented in other floating point specifications.
The advantages in speed offered by the fast inverse square root kludge came from treating the longwordUse of the type
long reduces the portability of this code on modern systems. For the code to execute properly, sizeof(long) must be 4 bytes, otherwise negative outputs may result. Under many modern 64-bit systems, sizeof(long) is 8 bytes. containing the floating point number as an integer then subtracting it from a specific constant, 0x5f3759df. The purpose of the constant is not immediately clear to someone viewing the code, so, like other such constants found in code, the number is often called "magic". This integer subtraction and bit shift results in an longword which when treated as a floating point number is a rough approximation for the inverse square root of the input number. One iteration of Newton's method is performed to gain some precision, and the code is finished. The algorithm generates reasonably accurate results using a unique first approximation for Newton's methodNewton's method
In numerical analysis, Newton's method , named after Isaac Newton and Joseph Raphson, is a method for finding successively better approximations to the roots of a real-valued function. The algorithm is first in the class of Householder's methods, succeeded by Halley's method...
, however it is much slower and less accurate than using the SSE
Streaming SIMD Extensions
In computing, Streaming SIMD Extensions is a SIMD instruction set extension to the x86 architecture, designed by Intel and introduced in 1999 in their Pentium III series processors as a reply to AMD's 3DNow! . SSE contains 70 new instructions, most of which work on single precision floating point...
instruction
rsqrtss on x86 processors, and also released in 1999.Aliasing from floating point to integer
Breaking this down requires some understanding of how a floating point number is stored. A floating point number represents a rational numberRational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
expressed in three portions across 32 bits. The first, the sign bit, is 0 for positive numbers and 1 for negative numbers. The next 8 bits form the exponent, which is biased
Exponent bias
In IEEE 754 floating point numbers, the exponent is biased in the engineering sense of the word – the value stored is offset from the actual value by the exponent bias....
in order to result in a range of values from −126 to 127. The significand
Significand
The significand is part of a floating-point number, consisting of its significant digits. Depending on the interpretation of the exponent, the significand may represent an integer or a fraction.-Examples:...
comprises the next 23 bits and represents the significant digits of the number stored. This is expressed as
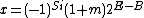where the bias 
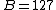. The value of the exponent determines whether the significand (referred to as the mantissa by Lomont 2003 and McEniry 2007) represents a fraction or an integer.A positive, signed integer
Integer (computer science)
In computer science, an integer is a datum of integral data type, a data type which represents some finite subset of the mathematical integers. Integral data types may be of different sizes and may or may not be allowed to contain negative values....
represented in a two's complement
Two's complement
The two's complement of a binary number is defined as the value obtained by subtracting the number from a large power of two...
system has a first bit of 0, followed by a binary representation of the value. Aliasing
Aliasing (computing)
In computing, aliasing describes a situation in which a data location in memory can be accessed through different symbolic names in the program. Thus, modifying the data through one name implicitly modifies the values associated to all aliased names, which may not be expected by the programmer...
the floating point number as a two-complement integer gives an integer value of
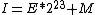where I is the integer value of the number, E the exponent and M the significand. Since the inverse square root function deals only with positive numbers, the floating point sign bit (Si) must be 0. This ensures that the resulting signed integer is also positive. The aliasing makes possible the computationally inexpensive operations that follow. The first of these, the 1-bit right shift, divides the integer by 2.The "magic number"
| S(ign) | E(xponent) | M(antissa) |
|---|---|---|
| 1 bit | b bits | (n-1-b) bits |
| n bits | ||
The selection of 0x5f3759df as a constant prompted much of the original speculation surrounding the fast inverse square root function. In an attempt to determine how a programmer might have originally determined that constant as a mechanism to approximate the inverse square root, Charles McEniry first determined how the choice of any constant R could give a first approximation for the inverse square root. Recalling the integer and floating point comparison from above, note that
, our floating point number, is 
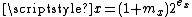and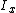 
, our integer value for that same number, is 
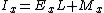.Floating point numbers are normalized—the significand is expressed as a number 
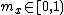. See for further explanation. These identities introduce a few new elements, which are simply restatements of values for the exponent and significand.
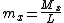where 
.
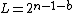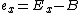where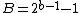 
.Per these identities, a bit shift operation and integer subtraction can reliably output an approximation for the inverse square root of a floating point number. The illustration from McEniry 2007 proceeds:
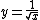
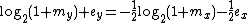
taking the binary logarithm
Binary logarithm
In mathematics, the binary logarithm is the logarithm to the base 2. It is the inverse function of n ↦ 2n. The binary logarithm of n is the power to which the number 2 must be raised to obtain the value n. This makes the binary logarithm useful for anything involving powers of 2,...
or
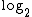of both sides. The binary logarithm is the inverse functionInverse function
In mathematics, an inverse function is a function that undoes another function: If an input x into the function ƒ produces an output y, then putting y into the inverse function g produces the output x, and vice versa. i.e., ƒ=y, and g=x...
of
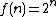and makes the multiplied terms in the floating point numbers x and y reduce to addition. The relationship between 
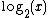and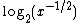 
is linear, allowing an equation to be constructed which can express x and 
(The input and first approximation) as a linear combinationLinear combination
In mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...
of terms. McEniry introduces a term
which serves as an approximation for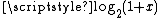 
in an intermediate step toward approximating R.Lomont 2003 approaches the determination of R in a different fashion, splitting R into 
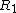and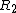 
for the significand and exponent bits of R. Since 
, 
, 
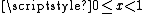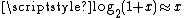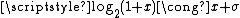can now be defined. This definition affords a first approximation of the binary logarithm. For our purposes, 
is a real numberReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
bounded by [0,1/3]—for an R equal to 0x5f3759df,
.
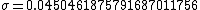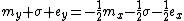
Using the identities for
, 
, 
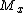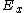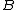and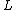 
:
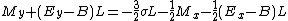
Rearranging of terms leads to:
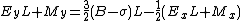
The integer value of a strictly positive floating point number x is
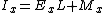. This gives an expression for the integer value of y (where 
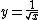, our first approximation for the inverse square root) in terms of the integer components of x. Specifically,
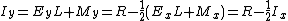where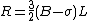 
.The equation
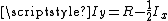is the line i = 0x5f3759df - (i>>1); in Fast InvSqrt, the integer approximation for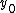 
is the integer value for x, shifted to the right and subtracted from R. McEniry's proof here shows only that a constant R can be used to approximate the integer value of the inverse square root of a floating point number. It does not prove that R assumes the value used in the code itself.A relatively simple explanation for how a bit shift and a subtraction operation using the expected value of R results in division of the exponent E by negative two can be found in Chris Lomont's paper exploring the constant. As an example, for
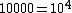, a division of the exponent by −2 would produce 
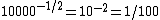. Since the exponent is biased, the true value of the exponent (here e) is 
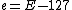, making the value of the biased result 
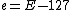. Subtracting the integer from R (the "magic" number 0x5f3759df) forces the least significant bit of the exponent to carry into the significand and when returned to floating point notation, outputs a floating point number very close to the inverse square root of the input. The specific value of R was chosen to minimize the expected error in division of the exponent as well as the expected error in shifting the significand. 0xbe represents an integer value which minimizes the expected error resulting from division of the floating point exponent through bit shift operations—notably the value of 0xbe shifted one to the right is 0x5f, the first digits in the magic number R.Accuracy
As noted above, the approximation is surprisingly accurate. The graph on the right plots the error of the function (that is, the error of the approximation after it has been improved by running one iteration of Newton's method), for inputs starting at 0.01, where the standard library gives 10.0 as a result, while InvSqrt gives 9.982522, making the difference 0.017479, or 0.175%. The absolute error only drops from then on, while the relative error stays within the same bounds across all orders of magnitude.Newton's method
After performing those integer operations, the algorithm once again treats the longword as a floating point number (x = *(float*)&i;) and performs a floating point multiplication operation (x = x*(1.5f - xhalf*x*x);). The floating point operation represents a single iteration of Newton's method of finding roots for a given equation. For this example,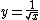
is the inverse square root, or, as a function of y,
.- As
represents a general expression of Newton's method with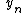 
as the first approximation,
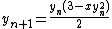is the particularized expression where 
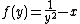and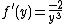 
.- Hence
x = x*(1.5f - xhalf*x*x);is the same as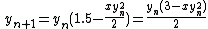
The first approximation is generated above through the integer operations and input into the last two lines of the function. Repeated iterations of the algorithm, using the output of the function (
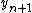) as the input of the next iteration, cause the algorithm to convergeRate of convergence
In numerical analysis, the speed at which a convergent sequence approaches its limit is called the rate of convergence. Although strictly speaking, a limit does not give information about any finite first part of the sequence, this concept is of practical importance if we deal with a sequence of...
on the root with increasing precision. For the purposes of the Quake III engine, only one iteration was used. A second iteration remained in the code but was commented out.
History and investigation
Usenet
Usenet is a worldwide distributed Internet discussion system. It developed from the general purpose UUCP architecture of the same name.Duke University graduate students Tom Truscott and Jim Ellis conceived the idea in 1979 and it was established in 1980...
and other forums as early as 2002 or 2003. Initial speculation pointed to John Carmack as the probable author of the code, but he demurred and suggested it was written by Terje Mathisen, an accomplished assembly programmer who had previously helped id Software with Quake optimization. Mathisen had written an implementation of a similar bit of code in the late 1990s, but the original authors proved to be much further back in the history of 3D computer graphics with Gary Tarolli's implementation for the SGI Indigo as a possible earliest known use. Jim Blinn also demonstrated a simple approximation of the inverse square root in a 1997 column for IEEE Computer Graphics and Applications. Rys Sommefeldt concluded that the original algorithm was devised by Greg Walsh at Ardent Computer
Ardent Computer
The Ardent Computer Corporation was a graphics minicomputer manufacturing company. The systems also used the Intel i860 as graphics co-processors. The company went through a series of mergers and re-organizations and changed names several times as their venture capital funders attempted to find a...
in consultation with Cleve Moler
Cleve Moler
Cleve Barry Moler is a mathematician and computer programmer specializing in numerical analysis. In the mid to late 1970s, he was one of the authors of LINPACK and EISPACK, Fortran libraries for numerical computing. He invented MATLAB, a numerical computing package, to give his students at the...
of MATLAB
MATLAB
MATLAB is a numerical computing environment and fourth-generation programming language. Developed by MathWorks, MATLAB allows matrix manipulations, plotting of functions and data, implementation of algorithms, creation of user interfaces, and interfacing with programs written in other languages,...
fame, though no conclusive proof of authorship exists.
It is not known precisely how the exact value for the magic number was determined. Chris Lomont developed a function to minimize approximation error
Approximation error
The approximation error in some data is the discrepancy between an exact value and some approximation to it. An approximation error can occur because#the measurement of the data is not precise due to the instruments...
by choosing the magic number R over a range. He first computed the optimal constant for the linear approximation step as 0x5f37642f, close to 0x5f3759df, but this new constant gave slightly less accuracy after one iteration of Newton's method. Lomont then searched for a constant optimal even after one and two Newton iterations and found 0x5f375a86, which is more accurate than the original at every iteration stage. He concluded by asking whether the exact value of the original constant was chosen through derivation or trial and error
Trial and error
Trial and error, or trial by error, is a general method of problem solving, fixing things, or for obtaining knowledge."Learning doesn't happen from failure itself but rather from analyzing the failure, making a change, and then trying again."...
. Lomont pointed out that the "magic number" for 64 bit IEEE754 size type double is 0x5fe6ec85e7de30da, but in fact it is close to 0x5fe6eb50c7aa19f9. Charles McEniry performed a similar but more sophisticated optimization over likely values for R. His initial brute force
Brute-force search
In computer science, brute-force search or exhaustive search, also known as generate and test, is a trivial but very general problem-solving technique that consists of systematically enumerating all possible candidates for the solution and checking whether each candidate satisfies the problem's...
search resulted in the same constant that Lomont determined. When he attempted to find the constant through weighted bisection
Bisection method
The bisection method in mathematics is a root-finding method which repeatedly bisects an interval and then selects a subinterval in which a root must lie for further processing. It is a very simple and robust method, but it is also relatively slow...
, the specific value of R used in the function occurred, leading McEniry to believe that the constant may have originally been derived through "bisecting to a given tolerance".
See also
- Methods of computing square roots: Approximations that depend on IEEE representation