Exotic sphere
Encyclopedia
In differential topology
, a mathematical discipline, an exotic sphere is a differentiable manifold
M that is homeomorphic but not diffeomorphic to the standard Euclidean n-sphere
. That is, M is a sphere from the point of view of all its topological properties, but carrying a smooth structure
that is not the familiar one (hence the name "exotic").
The first exotic spheres were constructed by in dimension n = 7 as S3-bundles over S4. He showed that there are at least 7 differentiable structures on the 7-sphere. In any dimension showed that the diffeomorphism classes of oriented exotic spheres form the non-trivial elements of an abelian monoid
under connected sum, which is a finite
abelian group
if the dimension is not 4. The classification of exotic spheres by Michel Kervaire
and John Milnor
(1963) showed that the oriented
exotic 7-spheres are the non-trivial elements of a cyclic group
of order 28 under the operation of connected sum
.
(x1, x2, ... xn+1) of real numbers, such that the sum x12 + x22 + ... + xn+12 = 1. (S1 is a circle; S2 is the surface of an ordinary ball of radius one in 3 dimensions.) Topologists consider a space, X, to be an n-sphere if every point in X can be assigned to exactly one point in the unit n-sphere in a continuous
way, which means that sufficiently nearby points in X get assigned to nearby points in Sn and vice-versa. For example a point x on an n-sphere of radius r can be matched with a point on the unit n-sphere by adjusting its distance from the origin by 1/r.
In differential topology
, a more stringent condition is added, that the functions matching points in X with points in Sn should be smooth
, that is they should have derivative
s of all orders everywhere. To calculate derivatives, one needs to have local coordinate systems defined consistently in X. Mathematicians were surprised in 1956 when John Milnor showed that consistent coordinate systems could be set up on the 7-sphere in two different ways that were equivalent in the continuous sense, but not in the differentiable sense. Milnor and others set about trying to discover how many such exotic spheres could exist in each dimension and to understand how they relate to each other. No exotic structures are possible on the 1-, 2-, 3-, 5-, 6- or 12-spheres. Some higher dimensional spheres have only two possible differentiable structures, others have thousands. Whether exotic 4-spheres exist, and if so how many, is an important unsolved problem in mathematics.
s on n-spheres is the collection of oriented smooth n-manifolds which are homeomorphic to the n-sphere, taken up to orientation-preserving diffeomorphism. The monoid operation is the connected sum
. Provided n ≠ 4, this monoid is a group and is isomorphic to the group Θn of h-cobordism
classes of oriented homotopy n-spheres
, which is finite and abelian. In dimension 4 almost nothing is known about the monoid of smooth spheres, beyond the facts that it is finite or countably infinite, and abelian, though it is suspected to be infinite; see the section on Gluck twists. All homotopy n-spheres are homeomorphic to the n-sphere by the generalized Poincaré conjecture
, proved by Stephen Smale
in dimensions bigger than 4, Michael Freedman
in dimension 4, and Grigori Perelman
in dimension 3. In dimension 3, Edwin E. Moise
proved that every topological manifold has an essentially unique smooth structure (see Moise's theorem
), so the monoid of smooth structures on the 3-sphere is trivial.
The group Θn has a cyclic subgroup
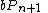
represented by n-spheres that bound parallelizable manifolds. The structures of bPn+1 and the quotient
are described separately in the paper , which was influential in the development of surgery theory
. In fact, these calculations can be formulated in a modern language in terms of the surgery exact sequence as indicated here.
The group bPn+1 is trivial if n is even. If n is 1 mod 4 it has order 1 or 2; in particular it has order 1 if n is 1, 5, 13, 29, or 61, and proved that it has order 2 if n = 1 mod 4 is not of the form 2k – 3.
The order of bP4n for n ≥ 2 is
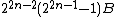
where B is the numerator of |4B2n/n|, and B2n is a Bernoulli number
. (The formula in the topological literature differs slightly because topologists use a different convention for naming Bernoulli numbers; this article uses the number theorists' convention.)
The quotient group Θn/bPn+1 has a description in terms of stable homotopy groups of spheres
modulo the image of the J-homomorphism
). More precisely there is an injective map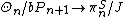
where πnS is the nth stable homotopy group of spheres, and J is the image of the J-homomorphism. proved this is an isomorphism if n is not of the form 2k – 2, and if n is of this form its image is either the whole group or a subgroup of index
2, and is a subgroup of index 2 in the first few cases when n is 2, 6, 14, 30, or 62. This index is 2 if and only if there exists an n-dimensional framed manifold with Kervaire invariant 1.
Finding the dimensions n in which this index is 2 is the Kervaire invariant problem, whose solution for all larger n except 126 was announced by Mike Hill, Michael Hopkins
and Doug Ravenel: the above list of dimensions can be extended by at most one, at most including 126.
The order of the group Θn is given in this table from (except that the entry for n = 19 is wrong by a factor of 2 in their paper; see the correction in volume III p. 97 of Milnor's collected works).
Further entries in this table can be computed from the information above together with the table of stable homotopy groups of spheres.
×S3, each with boundary
S3×S3, and glue them together by identifying (a,b) in the boundary with (a, a2ba−1), (where we identify each S3 with the group of unit quaternion
s). The resulting manifold has a natural smooth structure and is homeomorphic to S7, but is not diffeomorphic to S7. Milnor showed that it is not the boundary of any smooth 8-manifold with vanishing 4th Betti number, and has no orientation-reversing diffeomorphism to itself; either of these properties implies that it is not a standard 7-sphere. Milnor showed that this manifold has a Morse function with just two critical point
s, both non-degenerate, which implies that it is topologically a sphere.
As shown by (see also ) the intersection of the complex manifold
of points in C5 satisfying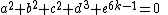
with a small sphere around the origin for k = 1, 2, ..., 28 gives all 28 possible smooth structures on the oriented 7-sphere.
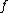yields a manifold called a twisted sphere (with twist f). It is homotopy equivalent to the standard n-sphere because the gluing map is homotopic to the identity (being an orientation-preserving diffeomorphism, hence degree 1), but not in general diffeomorphic to the standard sphere.
Setting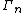
to be the group of twisted n-spheres (under connect sum), one obtains the exact sequence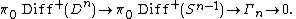
For n > 4, every exotic sphere is diffeomorphic to a twisted sphere, a result proven by Stephen Smale
. (In contrast, in the piecewise linear
setting the left-most map is onto via radial extension: there are no piecewise-linear-twisted spheres.) The group Γn of twisted spheres is always isomorphic
to the group Θn. The notations are different because it was not known at first that they were the same for n=3 or 4; for example, the case n=3 is equivalent to the Poincaré conjecture
.
In 1970 Jean Cerf proved the pseudoisotopy theorem
which implies that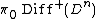
is the trivial group provided 
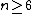, so 
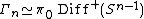provided 
.
then the problem of finding the compatible smooth structures on M depends on knowledge of the groups Γk = Θk. More precisely, the obstructions to the existence of any smooth structure lie in the groups Hk+1(M, Γk) for various values of k, while if such a smooth structure exists then all such smooth structures can be classified using the groups Hk(M, Γk).
In particular the groups Γk vanish if k<7, so all PL manifolds of dimension at most 7 have a smooth structure, which is essentially unique if the manifold has dimension at most 6.
The following finite abelian groups are essentially the same:
Some candidates for exotic 4-spheres are given by Gluck twists . These are constructed by cutting out a tubular neighborhood of a 2-sphere S in S4 and gluing it back in using a diffeomorphism of its boundary S2×S1. The result is always homeomorphic to S4. But in most cases it is unknown whether or not the result is diffeomorphic to S4. (If the 2-sphere is unknotted, or given by spinning a knot in the 3-sphere, then the Gluck twist is known to be diffeomorphic to S4, but there are plenty of other ways to knot a 2-sphere in S4.)
showed that a certain family of candidates for 4-dimensional exotic spheres constructed by Cappell and Shaneson are in fact standard.
Differential topology
In mathematics, differential topology is the field dealing with differentiable functions on differentiable manifolds. It is closely related to differential geometry and together they make up the geometric theory of differentiable manifolds.- Description :...
, a mathematical discipline, an exotic sphere is a differentiable manifold
Differentiable manifold
A differentiable manifold is a type of manifold that is locally similar enough to a linear space to allow one to do calculus. Any manifold can be described by a collection of charts, also known as an atlas. One may then apply ideas from calculus while working within the individual charts, since...
M that is homeomorphic but not diffeomorphic to the standard Euclidean n-sphere
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
. That is, M is a sphere from the point of view of all its topological properties, but carrying a smooth structure
Smooth structure
In mathematics, a smooth structure on a manifold allows for an unambiguous notion of smooth function. In particular, a smooth structure allows one to perform mathematical analysis on the manifold....
that is not the familiar one (hence the name "exotic").
The first exotic spheres were constructed by in dimension n = 7 as S3-bundles over S4. He showed that there are at least 7 differentiable structures on the 7-sphere. In any dimension showed that the diffeomorphism classes of oriented exotic spheres form the non-trivial elements of an abelian monoid
Monoid
In abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
under connected sum, which is a finite
Finite group
In mathematics and abstract algebra, a finite group is a group whose underlying set G has finitely many elements. During the twentieth century, mathematicians investigated certain aspects of the theory of finite groups in great depth, especially the local theory of finite groups, and the theory of...
abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
if the dimension is not 4. The classification of exotic spheres by Michel Kervaire
Michel Kervaire
Michel André Kervaire was a French mathematician who made significant contributions to topology and algebra. He was the first to show the existence of topological n-manifolds with no differentiable structure , and computed the number of exotic spheres in dimensions greater than four...
and John Milnor
John Milnor
John Willard Milnor is an American mathematician known for his work in differential topology, K-theory and dynamical systems. He won the Fields Medal in 1962, the Wolf Prize in 1989, and the Abel Prize in 2011. Milnor is a distinguished professor at Stony Brook University...
(1963) showed that the oriented
Orientability
In mathematics, orientability is a property of surfaces in Euclidean space measuring whether or not it is possible to make a consistent choice of surface normal vector at every point. A choice of surface normal allows one to use the right-hand rule to define a "clockwise" direction of loops in the...
exotic 7-spheres are the non-trivial elements of a cyclic group
Cyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
of order 28 under the operation of connected sum
Connected sum
In mathematics, specifically in topology, the operation of connected sum is a geometric modification on manifolds. Its effect is to join two given manifolds together near a chosen point on each...
.
Introduction
The unit n-sphere, Sn, is the set of all n+1-tuplesTuple
In mathematics and computer science, a tuple is an ordered list of elements. In set theory, an n-tuple is a sequence of n elements, where n is a positive integer. There is also one 0-tuple, an empty sequence. An n-tuple is defined inductively using the construction of an ordered pair...
(x1, x2, ... xn+1) of real numbers, such that the sum x12 + x22 + ... + xn+12 = 1. (S1 is a circle; S2 is the surface of an ordinary ball of radius one in 3 dimensions.) Topologists consider a space, X, to be an n-sphere if every point in X can be assigned to exactly one point in the unit n-sphere in a continuous
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
way, which means that sufficiently nearby points in X get assigned to nearby points in Sn and vice-versa. For example a point x on an n-sphere of radius r can be matched with a point on the unit n-sphere by adjusting its distance from the origin by 1/r.
In differential topology
Differential topology
In mathematics, differential topology is the field dealing with differentiable functions on differentiable manifolds. It is closely related to differential geometry and together they make up the geometric theory of differentiable manifolds.- Description :...
, a more stringent condition is added, that the functions matching points in X with points in Sn should be smooth
Smooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
, that is they should have derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
s of all orders everywhere. To calculate derivatives, one needs to have local coordinate systems defined consistently in X. Mathematicians were surprised in 1956 when John Milnor showed that consistent coordinate systems could be set up on the 7-sphere in two different ways that were equivalent in the continuous sense, but not in the differentiable sense. Milnor and others set about trying to discover how many such exotic spheres could exist in each dimension and to understand how they relate to each other. No exotic structures are possible on the 1-, 2-, 3-, 5-, 6- or 12-spheres. Some higher dimensional spheres have only two possible differentiable structures, others have thousands. Whether exotic 4-spheres exist, and if so how many, is an important unsolved problem in mathematics.
The monoid of smooth structures on spheres in a given dimension
The monoid of smooth structureSmooth structure
In mathematics, a smooth structure on a manifold allows for an unambiguous notion of smooth function. In particular, a smooth structure allows one to perform mathematical analysis on the manifold....
s on n-spheres is the collection of oriented smooth n-manifolds which are homeomorphic to the n-sphere, taken up to orientation-preserving diffeomorphism. The monoid operation is the connected sum
Connected sum
In mathematics, specifically in topology, the operation of connected sum is a geometric modification on manifolds. Its effect is to join two given manifolds together near a chosen point on each...
. Provided n ≠ 4, this monoid is a group and is isomorphic to the group Θn of h-cobordism
H-cobordism
A cobordism W between M and N is an h-cobordism if the inclusion mapsare homotopy equivalences...
classes of oriented homotopy n-spheres
Homotopy sphere
In algebraic topology, a branch of mathematics, a homotopy sphere is an n-manifold homotopy equivalent to the n-sphere. It thus has the same homotopy groups and the same homology groups, as the n-sphere...
, which is finite and abelian. In dimension 4 almost nothing is known about the monoid of smooth spheres, beyond the facts that it is finite or countably infinite, and abelian, though it is suspected to be infinite; see the section on Gluck twists. All homotopy n-spheres are homeomorphic to the n-sphere by the generalized Poincaré conjecture
Poincaré conjecture
In mathematics, the Poincaré conjecture is a theorem about the characterization of the three-dimensional sphere , which is the hypersphere that bounds the unit ball in four-dimensional space...
, proved by Stephen Smale
Stephen Smale
Steven Smale a.k.a. Steve Smale, Stephen Smale is an American mathematician from Flint, Michigan. He was awarded the Fields Medal in 1966, and spent more than three decades on the mathematics faculty of the University of California, Berkeley .-Education and career:He entered the University of...
in dimensions bigger than 4, Michael Freedman
Michael Freedman
Michael Hartley Freedman is a mathematician at Microsoft Station Q, a research group at the University of California, Santa Barbara. In 1986, he was awarded a Fields Medal for his work on the Poincaré conjecture. Freedman and Robion Kirby showed that an exotic R4 manifold exists.Freedman was born...
in dimension 4, and Grigori Perelman
Grigori Perelman
Grigori Yakovlevich Perelman is a Russian mathematician who has made landmark contributions to Riemannian geometry and geometric topology.In 1992, Perelman proved the soul conjecture. In 2002, he proved Thurston's geometrization conjecture...
in dimension 3. In dimension 3, Edwin E. Moise
Edwin E. Moise
Edwin Evariste Moise was an American mathematician and mathematics education reformer. After his retirement from mathematics he became a literary critic of 19th century English poetry and had several notes published in that field.-Early life and education:...
proved that every topological manifold has an essentially unique smooth structure (see Moise's theorem
Moise's theorem
In geometric topology, a branch of mathematics, Moise's theorem, proved by , states that any topological 3-manifold has an essentially unique piecewise-linear structure and smooth structure....
), so the monoid of smooth structures on the 3-sphere is trivial.
The group Θn has a cyclic subgroup
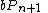
represented by n-spheres that bound parallelizable manifolds. The structures of bPn+1 and the quotient
are described separately in the paper , which was influential in the development of surgery theory
Surgery theory
In mathematics, specifically in geometric topology, surgery theory is a collection of techniques used to produce one manifold from another in a 'controlled' way, introduced by . Surgery refers to cutting out parts of the manifold and replacing it with a part of another manifold, matching up along...
. In fact, these calculations can be formulated in a modern language in terms of the surgery exact sequence as indicated here.
The group bPn+1 is trivial if n is even. If n is 1 mod 4 it has order 1 or 2; in particular it has order 1 if n is 1, 5, 13, 29, or 61, and proved that it has order 2 if n = 1 mod 4 is not of the form 2k – 3.
The order of bP4n for n ≥ 2 is
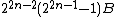
where B is the numerator of |4B2n/n|, and B2n is a Bernoulli number
Bernoulli number
In mathematics, the Bernoulli numbers Bn are a sequence of rational numbers with deep connections to number theory. They are closely related to the values of the Riemann zeta function at negative integers....
. (The formula in the topological literature differs slightly because topologists use a different convention for naming Bernoulli numbers; this article uses the number theorists' convention.)
The quotient group Θn/bPn+1 has a description in terms of stable homotopy groups of spheres
Homotopy groups of spheres
In the mathematical field of algebraic topology, the homotopy groups of spheres describe how spheres of various dimensions can wrap around each other. They are examples of topological invariants, which reflect, in algebraic terms, the structure of spheres viewed as topological spaces, forgetting...
modulo the image of the J-homomorphism
J-homomorphism
In mathematics, the J-homomorphism is a mapping from the homotopy groups of the special orthogonal groups to the homotopy groups of spheres. It was defined by , extending a construction of .-Definition:...
). More precisely there is an injective map
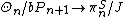
where πnS is the nth stable homotopy group of spheres, and J is the image of the J-homomorphism. proved this is an isomorphism if n is not of the form 2k – 2, and if n is of this form its image is either the whole group or a subgroup of index
Index of a subgroup
In mathematics, specifically group theory, the index of a subgroup H in a group G is the "relative size" of H in G: equivalently, the number of "copies" of H that fill up G. For example, if H has index 2 in G, then intuitively "half" of the elements of G lie in H...
2, and is a subgroup of index 2 in the first few cases when n is 2, 6, 14, 30, or 62. This index is 2 if and only if there exists an n-dimensional framed manifold with Kervaire invariant 1.
Finding the dimensions n in which this index is 2 is the Kervaire invariant problem, whose solution for all larger n except 126 was announced by Mike Hill, Michael Hopkins
Michael J. Hopkins
Michael Jerome Hopkins is an American mathematician known for work in algebraic topology.-Life:He received his Ph.D. from Northwestern University in 1984 under the direction of Mark Mahowald. In 1984 he also received his D.Phil...
and Doug Ravenel: the above list of dimensions can be extended by at most one, at most including 126.
The order of the group Θn is given in this table from (except that the entry for n = 19 is wrong by a factor of 2 in their paper; see the correction in volume III p. 97 of Milnor's collected works).
| Dim n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| order Θn | 1 | 1 | 1 | 1 | 1 | 1 | 28 | 2 | 8 | 6 | 992 | 1 | 3 | 2 | 16256 | 2 | 16 | 16 | 523264 | 24 |
| bPn+1 | 1 | 1 | 1 | 1 | 1 | 1 | 28 | 1 | 2 | 1 | 992 | 1 | 1 | 1 | 8128 | 1 | 2 | 1 | 261632 | 1 |
| Θn/bPn+1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 2 | 2×2 | 6 | 1 | 1 | 3 | 2 | 2 | 2 | 2×2×2 | 8×2 | 2 | 24 |
| πnS/J | 1 | 2 | 1 | 1 | 1 | 2 | 1 | 2 | 2×2 | 6 | 1 | 1 | 3 | 2×2 | 2 | 2 | 2×2×2 | 8×2 | 2 | 24 |
Further entries in this table can be computed from the information above together with the table of stable homotopy groups of spheres.
Explicit examples of exotic spheres
One of the first examples of an exotic sphere found by was the following: Take two copies of B4Ball (mathematics)
In mathematics, a ball is the space inside a sphere. It may be a closed ball or an open ball ....
×S3, each with boundary
Boundary (topology)
In topology and mathematics in general, the boundary of a subset S of a topological space X is the set of points which can be approached both from S and from the outside of S. More precisely, it is the set of points in the closure of S, not belonging to the interior of S. An element of the boundary...
S3×S3, and glue them together by identifying (a,b) in the boundary with (a, a2ba−1), (where we identify each S3 with the group of unit quaternion
Quaternion
In mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
s). The resulting manifold has a natural smooth structure and is homeomorphic to S7, but is not diffeomorphic to S7. Milnor showed that it is not the boundary of any smooth 8-manifold with vanishing 4th Betti number, and has no orientation-reversing diffeomorphism to itself; either of these properties implies that it is not a standard 7-sphere. Milnor showed that this manifold has a Morse function with just two critical point
Critical point
Critical point may refer to:*Critical point *Critical point *Critical point *Construction point of a ski jumping hill-See also:*Brillouin zone*Percolation thresholds...
s, both non-degenerate, which implies that it is topologically a sphere.
As shown by (see also ) the intersection of the complex manifold
Complex manifold
In differential geometry, a complex manifold is a manifold with an atlas of charts to the open unit disk in Cn, such that the transition maps are holomorphic....
of points in C5 satisfying
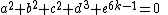
with a small sphere around the origin for k = 1, 2, ..., 28 gives all 28 possible smooth structures on the oriented 7-sphere.
Twisted spheres
Given an (orientation-preserving) diffeomorphism f: Sn−1→Sn−1, gluing the boundaries of two copies of the standard disk Dn together by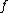 yields a manifold called a twisted sphere (with twist f). It is homotopy equivalent to the standard n-sphere because the gluing map is homotopic to the identity (being an orientation-preserving diffeomorphism, hence degree 1), but not in general diffeomorphic to the standard sphere. Setting
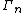to be the group of twisted n-spheres (under connect sum), one obtains the exact sequence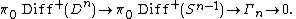For n > 4, every exotic sphere is diffeomorphic to a twisted sphere, a result proven by Stephen Smale
Stephen Smale
Steven Smale a.k.a. Steve Smale, Stephen Smale is an American mathematician from Flint, Michigan. He was awarded the Fields Medal in 1966, and spent more than three decades on the mathematics faculty of the University of California, Berkeley .-Education and career:He entered the University of...
. (In contrast, in the piecewise linear
Piecewise linear manifold
In mathematics, a piecewise linear manifold is a topological manifold together with a piecewise linear structure on it. Such a structure can be defined by means of an atlas, such that one can pass from chart to chart in it by piecewise linear functions.An isomorphism of PL manifolds is called a PL...
setting the left-most map is onto via radial extension: there are no piecewise-linear-twisted spheres.) The group Γn of twisted spheres is always isomorphic
to the group Θn. The notations are different because it was not known at first that they were the same for n=3 or 4; for example, the case n=3 is equivalent to the Poincaré conjecture
Poincaré conjecture
In mathematics, the Poincaré conjecture is a theorem about the characterization of the three-dimensional sphere , which is the hypersphere that bounds the unit ball in four-dimensional space...
.
In 1970 Jean Cerf proved the pseudoisotopy theorem
Pseudoisotopy theorem
In mathematics, the pseudoisotopy theorem is a theorem of Jean Cerf's which refers to the connectivity of a group of diffeomorphisms of a manifold.- Statement :...
which implies that
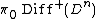is the trivial group provided 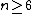, so 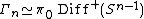provided .Applications
If M is a piecewise linear manifoldPiecewise linear manifold
In mathematics, a piecewise linear manifold is a topological manifold together with a piecewise linear structure on it. Such a structure can be defined by means of an atlas, such that one can pass from chart to chart in it by piecewise linear functions.An isomorphism of PL manifolds is called a PL...
then the problem of finding the compatible smooth structures on M depends on knowledge of the groups Γk = Θk. More precisely, the obstructions to the existence of any smooth structure lie in the groups Hk+1(M, Γk) for various values of k, while if such a smooth structure exists then all such smooth structures can be classified using the groups Hk(M, Γk).
In particular the groups Γk vanish if k<7, so all PL manifolds of dimension at most 7 have a smooth structure, which is essentially unique if the manifold has dimension at most 6.
The following finite abelian groups are essentially the same:
- The group Θn of h-cobordism classes of oriented homotopy n-spheres.
- The group of h-cobordism classes of oriented n-spheres.
- The group Γn of twisted oriented n spheres.
- The homotopy group πn(PL/DIFF)
- If n ≠ 3, the homotopy πn(TOP/DIFF) (if n=3 this group has order 2; see Kirby–Siebenmann invariant).
- The group of smooth structures of an oriented PL n-sphere.
- If n≠4, the group of smooth structures of an oriented topological n-sphere.
- If n≠5, the group of components of the group of all orientation-preserving diffeomorphisms of Sn−1.
4-dimensional exotic spheres and Gluck twists
In 4 dimensions it is not known whether there are any exotic smooth structures on the 4-sphere. The statement that they do not exist is known as the "smooth Poincaré conjecture", and is discussed by who say that it is believed to be false.Some candidates for exotic 4-spheres are given by Gluck twists . These are constructed by cutting out a tubular neighborhood of a 2-sphere S in S4 and gluing it back in using a diffeomorphism of its boundary S2×S1. The result is always homeomorphic to S4. But in most cases it is unknown whether or not the result is diffeomorphic to S4. (If the 2-sphere is unknotted, or given by spinning a knot in the 3-sphere, then the Gluck twist is known to be diffeomorphic to S4, but there are plenty of other ways to knot a 2-sphere in S4.)
showed that a certain family of candidates for 4-dimensional exotic spheres constructed by Cappell and Shaneson are in fact standard.
See also
- Atlas (topology)Atlas (topology)In mathematics, particularly topology, one describesa manifold using an atlas. An atlas consists of individualcharts that, roughly speaking, describe individual regionsof the manifold. If the manifold is the surface of the Earth,...
- Clutching constructionClutching constructionIn topology, a branch of mathematics, the clutching construction is a way of constructing fiber bundles, particularly vector bundles on spheres.-Definition:...
- Exotic R4Exotic R4In mathematics, an exotic R4 is a differentiable manifold that is homeomorphic to the Euclidean space R4, but not diffeomorphic.The first examples were found by Robion Kirby and Michael Freedman, by using the contrast between Freedman's theorems about topological 4-manifolds, and Simon Donaldson's...
- Cerf theoryCerf theoryIn mathematics, at the junction of singularity theory and differential topology, Cerf theory is the study of families of smooth real-valued functionsf:M \to \mathbb R...
- Seven-dimensional spaceSeven-dimensional spaceIn physics and mathematics, a sequence of n numbers can also be understood as a location in n-dimensional space. When n = 7, the set of all such locations is called 7-dimensional Euclidean space...
External links
- Exotic spheres on the Manifold Atlas.
- Exotic sphere home page on the home page of Andrew Ranicki. Assorted source material relating to exotic spheres.