
J-homomorphism
Encyclopedia
In mathematics
, the J-homomorphism is a mapping from the homotopy group
s of the special orthogonal groups to the homotopy groups of spheres
. It was defined by , extending a construction of .

of abelian groups for integers q, and r ≥ 2. (Hopf defined this for the special case q=r+1.)
The J-homomorphism can be defined as follows.
An element of the special orthogonal group SO(q) can be regarded as a map
and the homotopy group πr(SO(q)) consists of homotopy
-equivalence classes of maps from the r-sphere to SO(q).
Thus an element of πr(SO(q)) can be represented by a map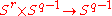
The suspension of this map give a map
On the other hand, there is a natural map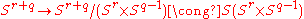
which contracts a copy of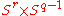 inside
inside  to a point, and composing these gives a map
to a point, and composing these gives a map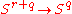
in πr+q(Sq), which Whitehead defined as the image of the element of πr(SO(q)) under the J-homomorphism.
The stable J-homomorphism in stable homotopy theory
gives a homomorphism

where SO is the infinite special orthogonal group, and the right-hand side is the r-th stable stem of the stable homotopy groups of spheres.
The group πr(SO) is given by Bott periodicity. It is always cyclic; and if r is positive, it is of order 2 if r is 0 or 1 mod 8, infinite if r is 3 mod 4, and order 1 otherwise . In particular the image of the stable J-homomorphism is cyclic. The stable homotopy groups πrS are the direct sum of the (cyclic) image of the J-homomorphism, and the kernel of the Adams e-invariant , a homomorphism from the stable homotopy groups to Q/Z. The order of the image is 2 if r is 0 or 1 mod 8 and positive (so in this case the J-homomorphism is injective). If r = 4n−1 is 3 mod 4 and positive the image is a cyclic group of order equal to the denominator of B2n/4n, where B2n is a Bernoulli number
. In the remaining cases where r is 2, 4, 5, or 6 mod 8 the image is trivial because πr(SO) is trivial.
The cokernel
of the J-homomorphism appears in the group of exotic sphere
s.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the J-homomorphism is a mapping from the homotopy group
Homotopy group
In mathematics, homotopy groups are used in algebraic topology to classify topological spaces. The first and simplest homotopy group is the fundamental group, which records information about loops in a space...
s of the special orthogonal groups to the homotopy groups of spheres
Homotopy groups of spheres
In the mathematical field of algebraic topology, the homotopy groups of spheres describe how spheres of various dimensions can wrap around each other. They are examples of topological invariants, which reflect, in algebraic terms, the structure of spheres viewed as topological spaces, forgetting...
. It was defined by , extending a construction of .
Definition
Whitehead's original homomorphism is defined geometrically, and gives a homomorphism
of abelian groups for integers q, and r ≥ 2. (Hopf defined this for the special case q=r+1.)
The J-homomorphism can be defined as follows.
An element of the special orthogonal group SO(q) can be regarded as a map

and the homotopy group πr(SO(q)) consists of homotopy
Homotopy
In topology, two continuous functions from one topological space to another are called homotopic if one can be "continuously deformed" into the other, such a deformation being called a homotopy between the two functions...
-equivalence classes of maps from the r-sphere to SO(q).
Thus an element of πr(SO(q)) can be represented by a map
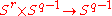
The suspension of this map give a map

On the other hand, there is a natural map
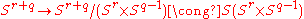
which contracts a copy of
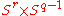 inside
inside  to a point, and composing these gives a map
to a point, and composing these gives a map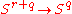
in πr+q(Sq), which Whitehead defined as the image of the element of πr(SO(q)) under the J-homomorphism.
The stable J-homomorphism in stable homotopy theory
Stable homotopy theory
In mathematics, stable homotopy theory is that part of homotopy theory concerned with all structure and phenomena that remain after sufficiently many applications of the suspension functor...
gives a homomorphism

where SO is the infinite special orthogonal group, and the right-hand side is the r-th stable stem of the stable homotopy groups of spheres.
Image of the J-homomorphism
The image of the J-homomorphism was described by , assuming the Adams conjecture of which was proved by , as follows.The group πr(SO) is given by Bott periodicity. It is always cyclic; and if r is positive, it is of order 2 if r is 0 or 1 mod 8, infinite if r is 3 mod 4, and order 1 otherwise . In particular the image of the stable J-homomorphism is cyclic. The stable homotopy groups πrS are the direct sum of the (cyclic) image of the J-homomorphism, and the kernel of the Adams e-invariant , a homomorphism from the stable homotopy groups to Q/Z. The order of the image is 2 if r is 0 or 1 mod 8 and positive (so in this case the J-homomorphism is injective). If r = 4n−1 is 3 mod 4 and positive the image is a cyclic group of order equal to the denominator of B2n/4n, where B2n is a Bernoulli number
Bernoulli number
In mathematics, the Bernoulli numbers Bn are a sequence of rational numbers with deep connections to number theory. They are closely related to the values of the Riemann zeta function at negative integers....
. In the remaining cases where r is 2, 4, 5, or 6 mod 8 the image is trivial because πr(SO) is trivial.
| r | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| πr(SO) | 1 | 2 | 1 | Z | 1 | 1 | 1 | Z | 2 | 2 | 1 | Z | 1 | 1 | 1 | Z | 2 | 2 |
| |im(J)| | 1 | 2 | 1 | 24 | 1 | 1 | 1 | 240 | 2 | 2 | 1 | 504 | 1 | 1 | 1 | 480 | 2 | 2 |
| πrS | Z | 2 | 2 | 24 | 1 | 1 | 2 | 240 | 22 | 23 | 6 | 504 | 1 | 3 | 22 | 480×2 | 22 | 24 |
| B2n | 1⁄6 | −1⁄30 | 1⁄42 | −1⁄30 |
Applications
introduced the group J(X) of a space X, which for X a sphere is the image of the J-homomorphism in a suitable dimension.The cokernel
Cokernel
In mathematics, the cokernel of a linear mapping of vector spaces f : X → Y is the quotient space Y/im of the codomain of f by the image of f....
of the J-homomorphism appears in the group of exotic sphere
Exotic sphere
In differential topology, a mathematical discipline, an exotic sphere is a differentiable manifold M that is homeomorphic but not diffeomorphic to the standard Euclidean n-sphere...
s.

