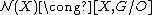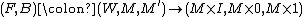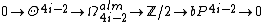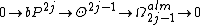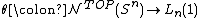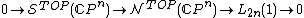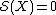Surgery exact sequence
Encyclopedia
In the mathematical surgery theory
the surgery exact sequence is the main technical tool to calculate the surgery structure set of a compact manifold
in dimension
. The surgery structure set 
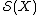of a compact 
-dimensional manifold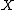 
is a pointed set which classifies 
-dimensional manifolds within the homotopy type of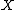 
.
The basic idea is that in order to calculate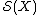
it is enough to understand the other terms in the sequence, which are usually easier to determine. These are on one hand the normal invariants
which form generalized cohomology groups, and hence one can use standard tools of algebraic topology to calculate them at least in principle. On the other hand there are the L-groups
which are defined algebraically in terms of quadratic forms or in terms of chain complexes with quadratic structure. A great deal is known about these groups. Another part of the sequence are the surgery obstruction maps from normal invariants to the L-groups. For these maps there are certain characteristic classes formulas, which enable to calculate them in some cases. Knowledge of these three components, that means: the normal maps, the L-groups and the surgery obstruction maps is enough to determine the structure set (at least up to extension problems).
In practice one has to proceed case by case, for each manifold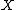
it is a unique task to determine the surgery exact sequence, see some examples below. Also note that there are versions of the surgery exact sequence depending on the category of manifolds we work with: smooth (DIFF), PL, or topological manifolds and whether we take Whitehead torsion into account or not (decorations 
or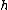 
).
The original 1962 work of Browder
and Novikov on the existence and uniqueness of manifolds within a simply-connected homotopy type was reformulated by Sullivan
in 1966 as a surgery exact sequence.
In 1970 Wall developed non-simply-connected surgery theory and the surgery exact sequence for manifolds with arbitrary fundamental group.
Surgery theory
In mathematics, specifically in geometric topology, surgery theory is a collection of techniques used to produce one manifold from another in a 'controlled' way, introduced by . Surgery refers to cutting out parts of the manifold and replacing it with a part of another manifold, matching up along...
the surgery exact sequence is the main technical tool to calculate the surgery structure set of a compact manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
in dimension
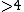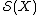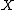. The surgery structure set of a compact -dimensional manifold is a pointed set which classifies -dimensional manifolds within the homotopy type of 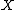.The basic idea is that in order to calculate
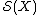it is enough to understand the other terms in the sequence, which are usually easier to determine. These are on one hand the normal invariantsNormal invariants
In mathematics, a normal map is a concept in geometric topology due to William Browder which is of fundamental importance in surgery theory. Given a Poincaré complex X, a normal map on X endows the space, roughly speaking, with some of the homotopy-theoretic global structure of a closed manifold...
which form generalized cohomology groups, and hence one can use standard tools of algebraic topology to calculate them at least in principle. On the other hand there are the L-groups
L-theory
Algebraic L-theory is the K-theory of quadratic forms; the term was coined by C. T. C. Wall,with L being used as the letter after K. Algebraic L-theory, also known as 'hermitian K-theory',is important in surgery theory.-Definition:...
which are defined algebraically in terms of quadratic forms or in terms of chain complexes with quadratic structure. A great deal is known about these groups. Another part of the sequence are the surgery obstruction maps from normal invariants to the L-groups. For these maps there are certain characteristic classes formulas, which enable to calculate them in some cases. Knowledge of these three components, that means: the normal maps, the L-groups and the surgery obstruction maps is enough to determine the structure set (at least up to extension problems).
In practice one has to proceed case by case, for each manifold
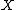it is a unique task to determine the surgery exact sequence, see some examples below. Also note that there are versions of the surgery exact sequence depending on the category of manifolds we work with: smooth (DIFF), PL, or topological manifolds and whether we take Whitehead torsion into account or not (decorations or 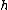).The original 1962 work of Browder
William Browder (mathematician)
William Browder is an American mathematician, specializing in algebraic topology, differential topology and differential geometry...
and Novikov on the existence and uniqueness of manifolds within a simply-connected homotopy type was reformulated by Sullivan
Dennis Sullivan
Dennis Parnell Sullivan is an American mathematician. He is known for work in topology, both algebraic and geometric, and on dynamical systems. He holds the Albert Einstein Chair at the City University of New York Graduate Center, and is a professor at Stony Brook University.-Work in topology:He...
in 1966 as a surgery exact sequence.
In 1970 Wall developed non-simply-connected surgery theory and the surgery exact sequence for manifolds with arbitrary fundamental group.
Definition
The surgery exact sequence is defined as-
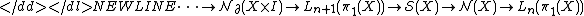
where:
the entries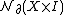
and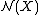 
are the abelian groups of normal invariantsNormal invariantsIn mathematics, a normal map is a concept in geometric topology due to William Browder which is of fundamental importance in surgery theory. Given a Poincaré complex X, a normal map on X endows the space, roughly speaking, with some of the homotopy-theoretic global structure of a closed manifold...
,
the entries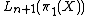
and 
are the L-groupsL-theoryAlgebraic L-theory is the K-theory of quadratic forms; the term was coined by C. T. C. Wall,with L being used as the letter after K. Algebraic L-theory, also known as 'hermitian K-theory',is important in surgery theory.-Definition:...
associated to the group ring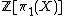
,
the maps
and 
are the surgery obstruction maps,
the arrows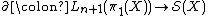
and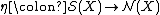 
will be explained below.
Versions
There are various versions of the surgery exact sequence. One can work in either of the three categories of manifolds: differentiable (smooth), PL, topological. Another possibility is to work with the decorations
or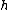 
.
Normal invariants
A degree one normal map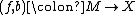
consists of the following data: an 
-dimensional oriented closed manifold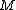 
, a map 
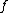which is of degree one (that means 
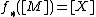, and a bundle map 
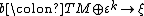from the stable tangent bundle of 
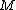to some bundle 
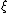over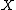 
. Two such maps are equivalent if there exists a normal bordism between them (that means a bordism of the sources covered by suitable bundle data). The equivalence classes of degree one normal maps are called normal invariants.
When defined like this the normal invariants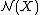
are just a pointed set, with the base point given by 
. However the Pontrjagin-Thom construction gives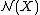 
a structure of an abelian group. In fact we have a non-natural bijection
where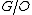
denotes the homotopy fiber of the map 
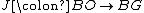, which is an infinite loop space and hence maps into it define a generalized cohomology theory. There are corresponding identifications of the normal invariants with 
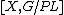when working with PL-manifolds and with 
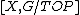when working with topological manifolds.
L-groups
The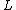
-groups are defined algebraically in terms of quadratic forms or in terms of chain complexes with quadratic structure. See the main article for more details. Here only the properties of the L-groups described below will be important.
Surgery obstruction maps
The map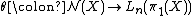
is in the first instance a set-theoretic map (that means not necessarily a homomorphism) with the following property (when 
:
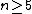A degree one normal map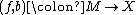
is normally cobordant to a homotopy equivalence if and only if the image 
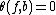in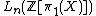 
.
The normal invariants arrow
Any homotopy equivalence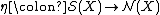
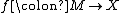defines a degree one normal map.
The surgery obstruction arrow
This arrow describes in fact an action of the group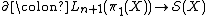
on the set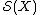 
rather than just a map. The definition is based on the realization theorem for the elements of the 
-groups which reads as follows:
Let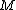
be an 
-dimensional manifold with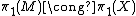 
and let 
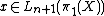. Then there exists a degree one normal map of manifolds with boundary
with the following properties:
1.
2.
is a diffeomorphism
3.
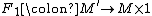is a homotopy equivalence of closed manifolds
Let
represent an element in 
and let 
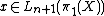. Then 
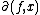is defined as 
.
The exactness
Recall that the surgery structure set is only a pointed set and that the surgery obstruction map
might not be a homomorphism. Hence it is necessary to explain what is meant when talking about the "exact sequence". So the surgery exact sequence is an exact sequence in the following sense:
For a normal invariant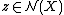
we have 
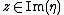if and only if 
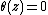. For two manifold structures 
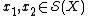we have 
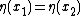if and only if there exists 
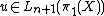such that 
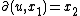. For an element 
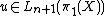we have 
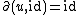if and only if 
.
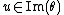Versions revisited
In the topological category the surgery obstruction map can be made into a homomorphism. This is achieved by putting an alternative abelian group structure on the normal invariants as described hereNormal invariantsIn mathematics, a normal map is a concept in geometric topology due to William Browder which is of fundamental importance in surgery theory. Given a Poincaré complex X, a normal map on X endows the space, roughly speaking, with some of the homotopy-theoretic global structure of a closed manifold...
. Moreover, the surgery exact sequence can be identified with the algebraic surgery exact sequence of Ranicki which is an exact sequence of abelian groups by definition. This gives the structure set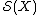
the structure of an abelian group. Note, however, that there is to this date no satisfactory geometric description of this abelian group structure.
Classification of manifolds
The answer to the organizing questions of the surgery theorySurgery theoryIn mathematics, specifically in geometric topology, surgery theory is a collection of techniques used to produce one manifold from another in a 'controlled' way, introduced by . Surgery refers to cutting out parts of the manifold and replacing it with a part of another manifold, matching up along...
can be formulated in terms of the surgery exact sequence. In both cases the answer is given in the form of a two-stage obstruction theory.
The existence question. Let
be a finite Poincaré complex. It is homotopy equivalent to a manifold if and only if the following two conditions are satisfied. Firstly,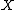 
must have a vector bundle reduction of its Spivak normal fibration. This condition can be also formulated as saying that the set of normal invariants 
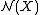is non-empty. Secondly, there must be a normal invariant 
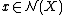such that 
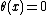. Equivalently, the surgery obstruction map 
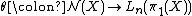hits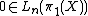 
.
The uniqueness question. Let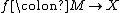
and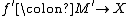 
represent two elements in the surgery structure set 
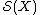. The question whether they represent the same element can be answered in two stages as follows. First there must be a normal cobordism between the degree one normal maps induced by 
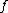and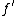 
, this means 
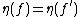in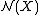 
. Denote the normal cobordism 
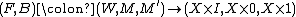. If the surgery obstruction 
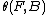in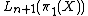 
to make this normal cobordism to an h-cobordismH-cobordismA cobordism W between M and N is an h-cobordism if the inclusion mapsare homotopy equivalences...
(or s-cobordism) relative to the boundary vanishes then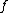
and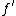 
in fact represent the same element in the surgery structure set.
1. Homotopy spheres
This is an example in the smooth category,Homotopy sphereIn algebraic topology, a branch of mathematics, a homotopy sphere is an n-manifold homotopy equivalent to the n-sphere. It thus has the same homotopy groups and the same homology groups, as the n-sphere...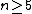
.
The idea of the surgery exact sequence is implicitly present already in the original article of Kervaire and Milnor on the groups of homotopy spheres. In the present terminology we have
the cobordism group of almost framed 
manifolds, 
where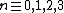 
mod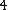 
(recall the 
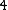-periodicity of the L-groupsL-theoryAlgebraic L-theory is the K-theory of quadratic forms; the term was coined by C. T. C. Wall,with L being used as the letter after K. Algebraic L-theory, also known as 'hermitian K-theory',is important in surgery theory.-Definition:...
)
The surgery exact sequence in this case is an exact sequence of abelian groups. In addition to the above identifications we have
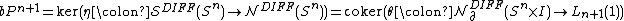
Because the odd-dimensional L-groups are trivial one obtains these exact sequences:
The results of Kervaire and Milnor are obtained by studying the middle map in the first two sequences and by relating the groups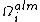
to stable homotopy theory.
2. Topological spheres
The generalized Poincaré conjectureGeneralized Poincaré conjectureIn the mathematical area of topology, the term Generalized Poincaré conjecture refers to a statement that a manifold which is a homotopy sphere 'is' a sphere. More precisely, one fixes a...
in dimension
can be phrased as saying that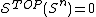 
. It has been proved for any 
by the work of Smale, Freedman and Perelman. From the surgery exact sequence for 
for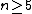 
in the topological category we see that
is an isomorphism. (In fact this can be extended to
by some ad-hoc methods.)
3. Complex projective spaces
The complex projective spaceProjective spaceIn mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
in the topological category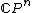
is a 
-dimensional topological manifold with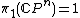 
. In addition it is known that in the case 
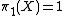in the topological category the surgery obstruction map 
is always surjective. Hence we have
From the work of Sullivan one can calculate
-
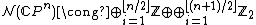and hence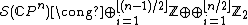 
4. Aspherical
An asphericalAsphericalAspherical may refer to:* Aspherical space, a concept in topology* Aspherical lens, a type of lens assembly used in photography which contains an aspheric lens...
manifolds in the topological category
-dimensional manifold 
is an 
-manifold such that 
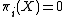for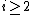 
. Hence the only non-trivial homotopy group is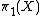 
One way to state the Borel conjectureBorel conjectureIn mathematics, specifically geometric topology, the Borel conjecture asserts that an aspherical closed manifold is determined by its fundamental group, up to homeomorphism...
is to say that for such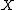
we have that the Whitehead groupWhitehead groupWhitehead group in mathematics may mean:* A group W with Ext=0; see Whitehead problem* For a ring, the Whitehead group Wh of a ring A, equal to K_1...
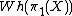is trivial and that
This conjecture was proven in many special cases - for example when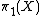
is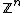 
, when it is the fundamental group of a negatively curved manifold or when it is a word-hyperbolic group or a CAT(0)-group.
The statement is equivalent to showing that the surgery obstruction map to the right of the surgery structure set is injective and the surgery obstruction map to the left of the surgery structure set is surjective. Most of the proofs of the above mentioned results are done by studying these maps or by studying the assembly mapsAssembly mapIn mathematics, assembly maps are an important concept in geometric topology. From the homotopy-theoretical viewpoint, an assembly map is a universal approximation of a homotopy invariant functor by a homology theory from the left...
with which they can be identified. See more details in Borel conjectureBorel conjectureIn mathematics, specifically geometric topology, the Borel conjecture asserts that an aspherical closed manifold is determined by its fundamental group, up to homeomorphism...
, Farrell-Jones Conjecture. -
