
Parallelizable manifold
Encyclopedia
In mathematics
, a parallelizable manifold is a smooth manifold of dimension n having vector field
is a smooth manifold of dimension n having vector field
s

such that at any point of
of  the tangent vector
the tangent vector
s
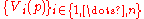
provide a basis of the tangent space
at . Equivalently, the tangent bundle
. Equivalently, the tangent bundle
is a trivial bundle, so that the associated principal bundle
of linear frames
has a section on .
.
A particular choice of such a basis of vector fields on is called a parallelization
is called a parallelization
(or an absolute parallelism) of .
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a parallelizable manifold
 is a smooth manifold of dimension n having vector field
is a smooth manifold of dimension n having vector fieldVector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
s

such that at any point
 of
of  the tangent vector
the tangent vectorTangent vector
A tangent vector is a vector that is tangent to a curve or surface at a given point.Tangent vectors are described in the differential geometry of curves in the context of curves in Rn. More generally, tangent vectors are elements of a tangent space of a differentiable manifold....
s
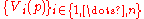
provide a basis of the tangent space
Tangent space
In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
at
 . Equivalently, the tangent bundle
. Equivalently, the tangent bundleTangent bundle
In differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
is a trivial bundle, so that the associated principal bundle
Principal bundle
In mathematics, a principal bundle is a mathematical object which formalizes some of the essential features of the Cartesian product X × G of a space X with a group G...
of linear frames
Frame bundle
In mathematics, a frame bundle is a principal fiber bundle F associated to any vector bundle E. The fiber of F over a point x is the set of all ordered bases, or frames, for Ex...
has a section on
 .
.A particular choice of such a basis of vector fields on
 is called a parallelization
is called a parallelizationParallelization (mathematics)
In mathematics, a parallelization of a manifold M\, of dimension n is a set of n global linearly independent vector fields.-Formal definition:...
(or an absolute parallelism) of
 .
.Examples
- An example with n = 1 is the circleCircleA circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
: we can take V1 to be the unit tangent vector field, say pointing in the anti-clockwise direction. The torusTorusIn geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
of dimension n is also parallelizable, as can be seen by expressing it as a cartesian productCartesian productIn mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
of circles. For example, take n = 2, and construct a torus from a square of graph paperGraph paperGraph paper, graphing paper, grid paper or millimeter paper is writing paper that is printed with fine lines making up a regular grid. The lines are often used as guides for plotting mathematical functions or experimental data and drawing diagrams. It is commonly found in mathematics and...
with opposite edges glued together, to get an idea of the two tangent directions at each point. More generally, any Lie groupLie groupIn mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
G is parallelizable, since a basis for the tangent space at the identity elementIdentity elementIn mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
can be moved around by the action of the translation group of G on G (any translation is a diffeomorphism and therefore these translations induce linear isomorphisms between tangent spaces of points in G).
- A classical problem was to determine which of the sphereSphereA sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
s Sn are parallelizable. The case S1 is the circle, which is parallelizable as has already been explained. The hairy ball theoremHairy ball theoremThe hairy ball theorem of algebraic topology states that there is no nonvanishing continuous tangent vector field on an even-dimensional n-sphere. An ordinary sphere is a 2-sphere, so that this theorem will hold for an ordinary sphere...
shows that S2 is not parallelizable. However S3 is parallelizable, since it is the Lie group SU(2). The only other parallelizable sphere is S7; this was proved in 1958, by Michel KervaireMichel KervaireMichel André Kervaire was a French mathematician who made significant contributions to topology and algebra. He was the first to show the existence of topological n-manifolds with no differentiable structure , and computed the number of exotic spheres in dimensions greater than four...
, and by Raoul BottRaoul BottRaoul Bott, FRS was a Hungarian mathematician known for numerous basic contributions to geometry in its broad sense...
and John MilnorJohn MilnorJohn Willard Milnor is an American mathematician known for his work in differential topology, K-theory and dynamical systems. He won the Fields Medal in 1962, the Wolf Prize in 1989, and the Abel Prize in 2011. Milnor is a distinguished professor at Stony Brook University...
, in independent work.
- Every Lie groupLie groupIn mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
is a parallelizable manifold.
- The product of parallelizable manifoldManifoldIn mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
s is parallelizable.
Remarks
- The term framed manifold (occasionally rigged manifold) is most usually applied to an embedded manifold with a given trivialisation of the normal bundleNormal bundleIn differential geometry, a field of mathematics, a normal bundle is a particular kind of vector bundle, complementary to the tangent bundle, and coming from an embedding .-Riemannian manifold:...
, and also for an abstract (i.e. non-embedded) manifold with a given stable trivialisation of the tangent bundleTangent bundleIn differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
.
See also
- Chart (topology)
- Differentiable manifoldDifferentiable manifoldA differentiable manifold is a type of manifold that is locally similar enough to a linear space to allow one to do calculus. Any manifold can be described by a collection of charts, also known as an atlas. One may then apply ideas from calculus while working within the individual charts, since...
- Frame bundleFrame bundleIn mathematics, a frame bundle is a principal fiber bundle F associated to any vector bundle E. The fiber of F over a point x is the set of all ordered bases, or frames, for Ex...
- Orthonormal frame bundle
- Principal bundlePrincipal bundleIn mathematics, a principal bundle is a mathematical object which formalizes some of the essential features of the Cartesian product X × G of a space X with a group G...
- Connection (mathematics)Connection (mathematics)In geometry, the notion of a connection makes precise the idea of transporting data along a curve or family of curves in a parallel and consistent manner. There are a variety of kinds of connections in modern geometry, depending on what sort of data one wants to transport...
- G-structureG-structureIn differential geometry, a G-structure on an n-manifold M, for a given structure group G, is a G-subbundle of the tangent frame bundle FM of M....

