
Hippopede
Encyclopedia
In geometry
, a hippopede (from ἱπποπέδη meaning "horse fetter" in ancient Greek) is a plane curve
determined by an equation of the form ,
,
where it is assumed that c>0 and c>d since the remaining cases either reduce to a single point or can be put into the given form with a rotation. Hippopedes are bicircular
rational algebraic curves
of degree 4 and symmetric with respect to both the x and y axes. When d>0 the curve has an oval form and is often known as an oval of Booth, and when d<0 the curve resembles a sideways figure eight, or lemniscate, and is often known as a lemniscate of Booth, after James Booth (1810–1878) who studied them. Hippopedes were also investigated by Proclus
(for whom they are sometimes called Hippopedes of Proclus) and Eudoxus
. For d = −c, the hippopede corresponds to the lemniscate of Bernoulli
.
and a plane, where the plane is parallel to the axis of the torus and tangent to it on the interior circle. Thus it is a spiric section
which in turn is a type of toric section
.
If a circle with radius a is rotated about an axis at distance b from its center, then the equation of the resulting hippopede in polar coordinates

or in Cartesian coordinates
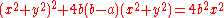 .
.
Note that when a>b the torus intersects itself, so it does not resemble the usual picture of a torus.
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, a hippopede (from ἱπποπέδη meaning "horse fetter" in ancient Greek) is a plane curve
Plane curve
In mathematics, a plane curve is a curve in a Euclidean plane . The most frequently studied cases are smooth plane curves , and algebraic plane curves....
determined by an equation of the form
 ,
,where it is assumed that c>0 and c>d since the remaining cases either reduce to a single point or can be put into the given form with a rotation. Hippopedes are bicircular
Circular algebraic curve
In geometry, a circular algebraic curve is a type of plane algebraic curve determined by an equation F = 0, where F is a polynomial with real coefficients and the highest-order terms of F form a polynomial divisible by x2 + y2...
rational algebraic curves
Algebraic curve
In algebraic geometry, an algebraic curve is an algebraic variety of dimension one. The theory of these curves in general was quite fully developed in the nineteenth century, after many particular examples had been considered, starting with circles and other conic sections.- Plane algebraic curves...
of degree 4 and symmetric with respect to both the x and y axes. When d>0 the curve has an oval form and is often known as an oval of Booth, and when d<0 the curve resembles a sideways figure eight, or lemniscate, and is often known as a lemniscate of Booth, after James Booth (1810–1878) who studied them. Hippopedes were also investigated by Proclus
Proclus
Proclus Lycaeus , called "The Successor" or "Diadochos" , was a Greek Neoplatonist philosopher, one of the last major Classical philosophers . He set forth one of the most elaborate and fully developed systems of Neoplatonism...
(for whom they are sometimes called Hippopedes of Proclus) and Eudoxus
Eudoxus
Eudoxus or Eudoxos was the name of two ancient Greeks:* Eudoxus of Cnidus , Greek astronomer and mathematician.* Eudoxus of Cyzicus , Greek navigator....
. For d = −c, the hippopede corresponds to the lemniscate of Bernoulli
Lemniscate of Bernoulli
In geometry, the lemniscate of Bernoulli is a plane curve defined from two given points F1 and F2, known as foci, at distance 2a from each other as the locus of points P so that PF1·PF2 = a2. The curve has a shape similar to the numeral 8 and to the ∞ symbol. Its name is from lemniscus, which is...
.
Definition as spiric sections
Hippopedes can be defined as the curve formed by the intersection of a torusTorus
In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
and a plane, where the plane is parallel to the axis of the torus and tangent to it on the interior circle. Thus it is a spiric section
Spiric section
In geometry, a spiric section, sometimes called a spiric of Perseus, is a quartic plane curve defined by equations of the form^2=dx^2+ey^2+f....
which in turn is a type of toric section
Toric section
A toric section is an intersection of a plane with a torus, just as a conic section is the intersection of a plane with a cone.-Mathematical formulae:In general, toric sections are fourth-order plane curves of the form...
.
If a circle with radius a is rotated about an axis at distance b from its center, then the equation of the resulting hippopede in polar coordinates

or in Cartesian coordinates
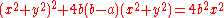 .
.Note that when a>b the torus intersects itself, so it does not resemble the usual picture of a torus.

