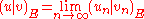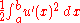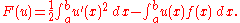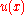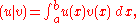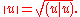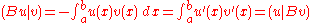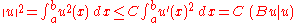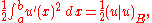Energetic space
Encyclopedia
In mathematics
, more precisely in functional analysis
, an energetic space is, intuitively, a subspace of a given real
Hilbert space
equipped with a new "energetic" inner product. The motivation for the name comes from physics
, as in many physical problems the energy
of a system can be expressed in terms of the energetic inner product. An example of this will be given later in the article.
 with the inner product
with the inner product  and the norm
and the norm
 . Let
. Let  be a linear subspace of
be a linear subspace of  and
and  be a strongly monotone symmetric linear operator, that is, a linear operator satisfying
be a strongly monotone symmetric linear operator, that is, a linear operator satisfying
The energetic inner product is defined as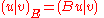 for all
for all  in
in 
and the energetic norm is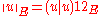 for all
for all  in
in 
The set together with the energetic inner product is a pre-Hilbert space. The energetic space
together with the energetic inner product is a pre-Hilbert space. The energetic space 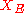 is defined as the completion of
is defined as the completion of  in the energetic norm.
in the energetic norm. 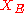 can be considered a subset of the original Hilbert space
can be considered a subset of the original Hilbert space 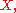 since any Cauchy sequence
since any Cauchy sequence
in the energetic norm is also Cauchy in the norm of (this follows from the strong monotonicity property of
(this follows from the strong monotonicity property of  ).
).
The energetic inner product is extended from to
to 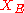 by
by
where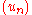 and
and 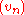 are sequences in Y that converge to points in
are sequences in Y that converge to points in 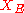 in the energetic norm.
in the energetic norm.
 admits an energetic extension
admits an energetic extension 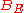
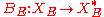
defined on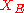 with values in the dual space
with values in the dual space
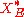 that is given by the formula
that is given by the formula
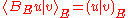 for all
for all  in
in 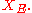
Here,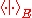 denotes the duality bracket between
denotes the duality bracket between 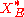 and
and 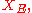 so
so 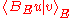 actually denotes
actually denotes 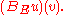
If and
and  are elements in the original subspace
are elements in the original subspace 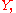 then
then
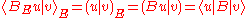
by the definition of the energetic inner product. If one views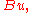 which is an element in
which is an element in 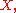 as an element in the dual
as an element in the dual 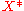 via the Riesz representation theorem
via the Riesz representation theorem
, then will also be in the dual
will also be in the dual 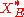 (by the strong monotonicity property of
(by the strong monotonicity property of  ). Via these identifications, it follows from the above formula that
). Via these identifications, it follows from the above formula that 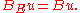 In different words, the original operator
In different words, the original operator  can be viewed as an operator
can be viewed as an operator  and then
and then 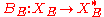 is simply the function extension of
is simply the function extension of  from
from  to
to 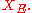
 Consider a string
Consider a string
whose endpoints are fixed at two points on the real line (here viewed as a horizontal line). Let the vertical outer force density
on the real line (here viewed as a horizontal line). Let the vertical outer force density
at each point
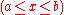 on the string be
on the string be  , where
, where  is a unit vector pointing vertically and
is a unit vector pointing vertically and 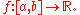 Let
Let 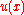 be the deflection
be the deflection
of the string at the point under the influence of the force. Assuming that the deflection is small, the elastic energy
under the influence of the force. Assuming that the deflection is small, the elastic energy
of the string is
and the total potential energy
of the string is
The deflection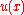 minimizing the potential energy will satisfy the differential equation
minimizing the potential energy will satisfy the differential equation
with boundary conditions
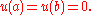
To study this equation, consider the space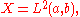 that is, the Lp space
that is, the Lp space
of all square integrable functions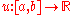 in respect to the Lebesgue measure
in respect to the Lebesgue measure
. This space is Hilbert in respect to the inner product
with the norm being given by
Let be the set of all twice continuously differentiable functions
be the set of all twice continuously differentiable functions
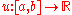 with the boundary conditionss
with the boundary conditionss 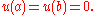 Then
Then  is a linear subspace of
is a linear subspace of 
Consider the operator given by the formula
given by the formula
so the deflection satisfies the equation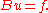 Using integration by parts
Using integration by parts
and the boundary conditions, one can see that
for any and
and  in
in  Therefore,
Therefore,  is a symmetric linear operator.
is a symmetric linear operator.
 is also strongly monotone, since, by the Friedrichs' inequality
is also strongly monotone, since, by the Friedrichs' inequality
for some
The energetic space in respect to the operator is then the Sobolev space
is then the Sobolev space
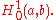 We see that the elastic energy of the string which motivated this study is
We see that the elastic energy of the string which motivated this study is
so it is half of the energetic inner product of with itself.
with itself.
To calculate the deflection minimizing the total potential energy
minimizing the total potential energy 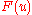 of the string, one writes this problem in the form
of the string, one writes this problem in the form
 for all
for all  in
in 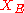 .
.
Next, one usually approximates by some
by some 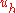 , a function in a finite-dimensional subspace of the true solution space. For example, one might let
, a function in a finite-dimensional subspace of the true solution space. For example, one might let 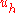 be a continuous piecewise-linear function in the energetic space, which gives the finite element method
be a continuous piecewise-linear function in the energetic space, which gives the finite element method
. The approximation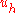 can be computed by solving a linear system of equations.
can be computed by solving a linear system of equations.
The energetic norm turns out to be the natural norm in which to measure the error between and
and 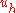 , see Céa's lemma
, see Céa's lemma
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, more precisely in functional analysis
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
, an energetic space is, intuitively, a subspace of a given real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
equipped with a new "energetic" inner product. The motivation for the name comes from physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, as in many physical problems the energy
Energy
In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
of a system can be expressed in terms of the energetic inner product. An example of this will be given later in the article.
Energetic space
Formally, consider a real Hilbert space with the inner product
with the inner product  and the norm
and the normNorm (mathematics)
In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
 . Let
. Let  be a linear subspace of
be a linear subspace of  and
and  be a strongly monotone symmetric linear operator, that is, a linear operator satisfying
be a strongly monotone symmetric linear operator, that is, a linear operator satisfying-
 for all
for all  in
in 
-
 for some constant
for some constant  and all
and all  in
in 
The energetic inner product is defined as
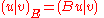 for all
for all  in
in 
and the energetic norm is
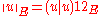 for all
for all  in
in 
The set
 together with the energetic inner product is a pre-Hilbert space. The energetic space
together with the energetic inner product is a pre-Hilbert space. The energetic space 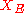 is defined as the completion of
is defined as the completion of  in the energetic norm.
in the energetic norm. 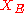 can be considered a subset of the original Hilbert space
can be considered a subset of the original Hilbert space 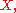 since any Cauchy sequence
since any Cauchy sequenceCauchy sequence
In mathematics, a Cauchy sequence , named after Augustin-Louis Cauchy, is a sequence whose elements become arbitrarily close to each other as the sequence progresses...
in the energetic norm is also Cauchy in the norm of
 (this follows from the strong monotonicity property of
(this follows from the strong monotonicity property of  ).
).The energetic inner product is extended from
 to
to 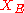 by
by
where
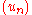 and
and 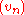 are sequences in Y that converge to points in
are sequences in Y that converge to points in 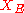 in the energetic norm.
in the energetic norm.Energetic extension
The operator admits an energetic extension
admits an energetic extension 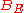
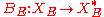
defined on
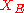 with values in the dual space
with values in the dual spaceDual space
In mathematics, any vector space, V, has a corresponding dual vector space consisting of all linear functionals on V. Dual vector spaces defined on finite-dimensional vector spaces can be used for defining tensors which are studied in tensor algebra...
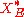 that is given by the formula
that is given by the formula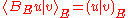 for all
for all  in
in 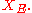
Here,
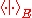 denotes the duality bracket between
denotes the duality bracket between 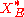 and
and 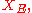 so
so 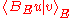 actually denotes
actually denotes 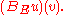
If
 and
and  are elements in the original subspace
are elements in the original subspace 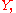 then
then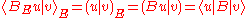
by the definition of the energetic inner product. If one views
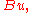 which is an element in
which is an element in 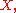 as an element in the dual
as an element in the dual 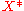 via the Riesz representation theorem
via the Riesz representation theoremRiesz representation theorem
There are several well-known theorems in functional analysis known as the Riesz representation theorem. They are named in honour of Frigyes Riesz.- The Hilbert space representation theorem :...
, then
 will also be in the dual
will also be in the dual 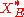 (by the strong monotonicity property of
(by the strong monotonicity property of  ). Via these identifications, it follows from the above formula that
). Via these identifications, it follows from the above formula that 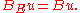 In different words, the original operator
In different words, the original operator  can be viewed as an operator
can be viewed as an operator  and then
and then 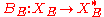 is simply the function extension of
is simply the function extension of  from
from  to
to 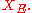
An example from physics

Rope
A rope is a length of fibres, twisted or braided together to improve strength for pulling and connecting. It has tensile strength but is too flexible to provide compressive strength...
whose endpoints are fixed at two points
 on the real line (here viewed as a horizontal line). Let the vertical outer force density
on the real line (here viewed as a horizontal line). Let the vertical outer force densityForce density
In fluid mechanics, the force density is the negative gradient of pressure. It has the physical dimensions of force per unit volume. Force density is a vector field representing the flux density of the hydrostatic force within the bulk of a fluid...
at each point

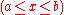 on the string be
on the string be  , where
, where  is a unit vector pointing vertically and
is a unit vector pointing vertically and 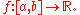 Let
Let 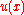 be the deflection
be the deflectionDeflection
Deflection or deflexion may refer to:* Deflection , the displacement of a structural element under load* Deflection , a technique of shooting ahead of a moving target so that the target and projectile will collide...
of the string at the point
 under the influence of the force. Assuming that the deflection is small, the elastic energy
under the influence of the force. Assuming that the deflection is small, the elastic energyElastic energy
Elastic energy is the potential mechanical energy stored in the configuration of a material or physical system as work is performed to distort its volume or shape....
of the string is
and the total potential energy
Potential energy
In physics, potential energy is the energy stored in a body or in a system due to its position in a force field or due to its configuration. The SI unit of measure for energy and work is the Joule...
of the string is
The deflection
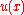 minimizing the potential energy will satisfy the differential equation
minimizing the potential energy will satisfy the differential equationDifferential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
with boundary conditions
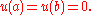
To study this equation, consider the space
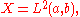 that is, the Lp space
that is, the Lp spaceLp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
of all square integrable functions
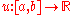 in respect to the Lebesgue measure
in respect to the Lebesgue measureLebesgue measure
In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
. This space is Hilbert in respect to the inner product
with the norm being given by
Let
 be the set of all twice continuously differentiable functions
be the set of all twice continuously differentiable functionsSmooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
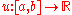 with the boundary conditionss
with the boundary conditionss 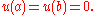 Then
Then  is a linear subspace of
is a linear subspace of 
Consider the operator
 given by the formula
given by the formulaso the deflection satisfies the equation
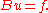 Using integration by parts
Using integration by partsIntegration by parts
In calculus, and more generally in mathematical analysis, integration by parts is a rule that transforms the integral of products of functions into other integrals...
and the boundary conditions, one can see that
for any
 and
and  in
in  Therefore,
Therefore,  is a symmetric linear operator.
is a symmetric linear operator. is also strongly monotone, since, by the Friedrichs' inequality
is also strongly monotone, since, by the Friedrichs' inequalityFriedrichs' inequality
In mathematics, Friedrichs' inequality is a theorem of functional analysis, due to Kurt Friedrichs. It places a bound on the Lp norm of a function using Lp bounds on the weak derivatives of the function and the geometry of the domain, and can be used to show that certain norms on Sobolev spaces are...
for some

The energetic space in respect to the operator
 is then the Sobolev space
is then the Sobolev spaceSobolev space
In mathematics, a Sobolev space is a vector space of functions equipped with a norm that is a combination of Lp-norms of the function itself as well as its derivatives up to a given order. The derivatives are understood in a suitable weak sense to make the space complete, thus a Banach space...
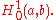 We see that the elastic energy of the string which motivated this study is
We see that the elastic energy of the string which motivated this study isso it is half of the energetic inner product of
 with itself.
with itself.To calculate the deflection
 minimizing the total potential energy
minimizing the total potential energy 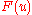 of the string, one writes this problem in the form
of the string, one writes this problem in the form for all
for all  in
in 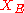 .
.Next, one usually approximates
 by some
by some 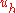 , a function in a finite-dimensional subspace of the true solution space. For example, one might let
, a function in a finite-dimensional subspace of the true solution space. For example, one might let 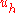 be a continuous piecewise-linear function in the energetic space, which gives the finite element method
be a continuous piecewise-linear function in the energetic space, which gives the finite element methodFinite element method
The finite element method is a numerical technique for finding approximate solutions of partial differential equations as well as integral equations...
. The approximation
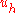 can be computed by solving a linear system of equations.
can be computed by solving a linear system of equations.The energetic norm turns out to be the natural norm in which to measure the error between
 and
and 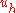 , see Céa's lemma
, see Céa's lemmaCéa's lemma
Céa's lemma is a lemma in mathematics. It is an important tool for proving error estimates for the finite element method applied to elliptic partial differential equations.-Lemma statement:Let V be a real Hilbert space with the norm \|\cdot\|...
.