Strongly monotone
Encyclopedia
In functional analysis
, an operator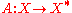
where X is a real Hilbert space
is said to be strongly monotone if
This is analogous to the notion of strictly increasing for scalar-valued functions of one scalar argument.
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
, an operator
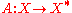where X is a real Hilbert spaceHilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
is said to be strongly monotone if
This is analogous to the notion of strictly increasing for scalar-valued functions of one scalar argument.