Bernoulli process
Encyclopedia
In probability
and statistics
, a Bernoulli process is a finite or infinite sequence of binary random variable
s, so it is a discrete-time
stochastic process
that takes only two values, canonically 0 and 1. The component Bernoulli variables Xi are identical and independent
. Prosaically, a Bernoulli process is repeated coin flipping
, possibly with an unfair coin - but one whose unfairness is constant.
Every variable Xi in the sequence may be associated with a Bernoulli trial
or experiment. They all have the same Bernoulli distribution.
The problem of determining the process, given only a limited sample of the Bernoulli trials, may be called the problem of checking if a coin is fair.
random variable
s X1, X2, X3, ..., such that
In other words, a Bernoulli process is a sequence of independent identically distributed Bernoulli trial
s.
Independence of the trials implies that the process is memoryless. Given that the probability p is known, past outcomes provide no information about future outcomes. (If p is unknown, however, the past informs about the future indirectly, through inferences about p.)
If the process is infinite, then from any point the future trials constitute a Bernoulli process identical to the whole process, the fresh-start property.
Two other common interpretations of the values are true or false and yes or no. Under any interpretation of the two values, the individual variables Xi may be called Bernoulli trial
s with parameter p.
In many applications time passes between trials, as the index i increases. In effect, the trials X1, X2, ... Xi, ... happen at "points in time" 1, 2, ..., i, .... That passage of time and the associated notions of "past" and "future" are not necessary, however. Most generally, any Xi and Xj in the process are simply two from a set of random variables indexed by {1, 2, ..., n} or by {1, 2, 3, ...}, the finite and infinite cases.
Several random variables and probability distributions beside the Bernoullis may be derived from the Bernoulli process:
The negative binomial variables may be interpreted as random waiting times.
s as a random sequence in {0, 1}, a single random variable.
A Bernoulli process is then a probability triple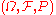
and a random variable
X mapping Ω into the set {0, 1}N such that for every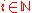
, one has 
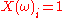with probability p and 
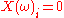with probability 1 − p.
Where there is no possible confusion, Xi(ω) may be written Xi.
of a Bernoulli process.
However, the term has an entirely different formal definition as given below.
Suppose a Bernoulli process formally defined as a single random variable (see preceding section). For every
there is a sequence
of integers
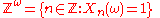
called the Bernoulli sequence associated with the Bernoulli process. For example, if ω represents a sequence of coin flips, then the associated Bernoulli sequence is the list of natural numbers or time-points for which the coin toss outcome is heads.
So defined, a Bernoulli sequence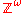
is also a random subset of the index set, the natural numbers 
.
Almost all
Bernoulli sequences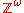
are ergodic sequences.
, which actually extracts uniform randomness.
Represent the observed process as a sequence of zeroes and ones, or bits, and group that input stream in non-overlapping pairs of successive bits, such as (11)(00)(10)... . Then for each pair,
This table summarizes the computation.
In the output stream 0 and 1 are equally likely, as 10 and 01 are equally likely in the original, both having probability pq = qp. This extraction of uniform randomness does not require the input trials to be independent, only uncorrelated
. More generally, it works for any exchangeable sequence of bits: all sequences that are finite rearrangements are equally likely.
The Von Neumann extractor uses two input bits to produce either zero or one output bits, so the output is shorter than the input by a factor of at least 2. On average the computation discards proportion p2 + (1 − p)2 of the input pairs, or proportion p2 + q2, which is near one when p is near zero or one.
The discard of input pairs is at least proportion 1/2, the minimum which occurs where p = 1/2 for the original process. In that case the output stream is 1/4 the length of the input on average.
.
Probability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
and statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, a Bernoulli process is a finite or infinite sequence of binary random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s, so it is a discrete-time
Discrete time
Discrete time is the discontinuity of a function's time domain that results from sampling a variable at a finite interval. For example, consider a newspaper that reports the price of crude oil once every day at 6:00AM. The newspaper is described as sampling the cost at a frequency of once per 24...
stochastic process
Stochastic process
In probability theory, a stochastic process , or sometimes random process, is the counterpart to a deterministic process...
that takes only two values, canonically 0 and 1. The component Bernoulli variables Xi are identical and independent
Statistical independence
In probability theory, to say that two events are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs...
. Prosaically, a Bernoulli process is repeated coin flipping
Coin flipping
Coin flipping or coin tossing or heads or tails is the practice of throwing a coin in the air to choose between two alternatives, sometimes to resolve a dispute between two parties...
, possibly with an unfair coin - but one whose unfairness is constant.
Every variable Xi in the sequence may be associated with a Bernoulli trial
Bernoulli trial
In the theory of probability and statistics, a Bernoulli trial is an experiment whose outcome is random and can be either of two possible outcomes, "success" and "failure"....
or experiment. They all have the same Bernoulli distribution.
The problem of determining the process, given only a limited sample of the Bernoulli trials, may be called the problem of checking if a coin is fair.
Definition
A Bernoulli process is a finite or infinite sequence of independentStatistical independence
In probability theory, to say that two events are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs...
random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s X1, X2, X3, ..., such that
- For each i, the value of Xi is either 0 or 1;
- For all values of i, the probability that Xi = 1 is the same number p.
In other words, a Bernoulli process is a sequence of independent identically distributed Bernoulli trial
Bernoulli trial
In the theory of probability and statistics, a Bernoulli trial is an experiment whose outcome is random and can be either of two possible outcomes, "success" and "failure"....
s.
Independence of the trials implies that the process is memoryless. Given that the probability p is known, past outcomes provide no information about future outcomes. (If p is unknown, however, the past informs about the future indirectly, through inferences about p.)
If the process is infinite, then from any point the future trials constitute a Bernoulli process identical to the whole process, the fresh-start property.
Interpretation
The two possible values of each Xi are often called "success" and "failure". Thus, when expressed as a number 0 or 1, the outcome may be called the number of successes on the ith "trial".Two other common interpretations of the values are true or false and yes or no. Under any interpretation of the two values, the individual variables Xi may be called Bernoulli trial
Bernoulli trial
In the theory of probability and statistics, a Bernoulli trial is an experiment whose outcome is random and can be either of two possible outcomes, "success" and "failure"....
s with parameter p.
In many applications time passes between trials, as the index i increases. In effect, the trials X1, X2, ... Xi, ... happen at "points in time" 1, 2, ..., i, .... That passage of time and the associated notions of "past" and "future" are not necessary, however. Most generally, any Xi and Xj in the process are simply two from a set of random variables indexed by {1, 2, ..., n} or by {1, 2, 3, ...}, the finite and infinite cases.
Several random variables and probability distributions beside the Bernoullis may be derived from the Bernoulli process:
- The number of successes in the first n trials, which has a binomial distribution B(n, p)
- The number of trials needed to get r successes, which has a negative binomial distributionNegative binomial distributionIn probability theory and statistics, the negative binomial distribution is a discrete probability distribution of the number of successes in a sequence of Bernoulli trials before a specified number of failures occur...
NB(r, p) - The number of trials needed to get one success, which has a geometric distribution NB(1, p), a special case of the negative binomial distribution
The negative binomial variables may be interpreted as random waiting times.
Formal definition
The Bernoulli process can be formalized in the language of probability spaceProbability space
In probability theory, a probability space or a probability triple is a mathematical construct that models a real-world process consisting of states that occur randomly. A probability space is constructed with a specific kind of situation or experiment in mind...
s as a random sequence in {0, 1}, a single random variable.
A Bernoulli process is then a probability triple
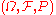and a random variableRandom variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
X mapping Ω into the set {0, 1}N such that for every
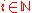, one has 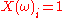with probability p and 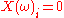with probability 1 − p.Where there is no possible confusion, Xi(ω) may be written Xi.
Bernoulli sequence
The term Bernoulli sequence is often used informally to refer to a realizationRealization (probability)
In probability and statistics, a realization, or observed value, of a random variable is the value that is actually observed . The random variable itself should be thought of as the process how the observation comes about...
of a Bernoulli process.
However, the term has an entirely different formal definition as given below.
Suppose a Bernoulli process formally defined as a single random variable (see preceding section). For every
there is a sequenceSequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
of integers
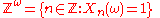
called the Bernoulli sequence associated with the Bernoulli process. For example, if ω represents a sequence of coin flips, then the associated Bernoulli sequence is the list of natural numbers or time-points for which the coin toss outcome is heads.
So defined, a Bernoulli sequence
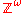is also a random subset of the index set, the natural numbers .Almost all
Almost all
In mathematics, the phrase "almost all" has a number of specialised uses."Almost all" is sometimes used synonymously with "all but finitely many" or "all but a countable set" ; see almost....
Bernoulli sequences
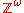are ergodic sequences.Randomness extraction
From any Bernoulli process one may derive a Bernoulli process with p = 1/2 by the von Neumann extractor, the earliest randomness extractorRandomness extractor
A randomness extractor, often simply called "an extractor," is a function which, when applied to a high-entropy source , generates a random output that is shorter, but uniformly distributed...
, which actually extracts uniform randomness.
Represent the observed process as a sequence of zeroes and ones, or bits, and group that input stream in non-overlapping pairs of successive bits, such as (11)(00)(10)... . Then for each pair,
- if the bits are equal, discard;
- if the bits are not equal, output the first bit.
This table summarizes the computation.
| input | output |
|---|---|
| 00 | discard |
| 01 | 0 |
| 10 | 1 |
| 11 | discard |
In the output stream 0 and 1 are equally likely, as 10 and 01 are equally likely in the original, both having probability pq = qp. This extraction of uniform randomness does not require the input trials to be independent, only uncorrelated
Uncorrelated
In probability theory and statistics, two real-valued random variables are said to be uncorrelated if their covariance is zero. Uncorrelatedness is by definition pairwise; i.e...
. More generally, it works for any exchangeable sequence of bits: all sequences that are finite rearrangements are equally likely.
The Von Neumann extractor uses two input bits to produce either zero or one output bits, so the output is shorter than the input by a factor of at least 2. On average the computation discards proportion p2 + (1 − p)2 of the input pairs, or proportion p2 + q2, which is near one when p is near zero or one.
The discard of input pairs is at least proportion 1/2, the minimum which occurs where p = 1/2 for the original process. In that case the output stream is 1/4 the length of the input on average.
Generalizations
The generalization of the Bernoulli process to more than two possible outcomes is called the Bernoulli schemeBernoulli scheme
In mathematics, the Bernoulli scheme or Bernoulli shift is a generalization of the Bernoulli process to more than two possible outcomes. Bernoulli schemes are important in the study of dynamical systems, as most such systems exhibit a repellor that is the product of the Cantor set and a smooth...
.
See also
- Bernoulli schemeBernoulli schemeIn mathematics, the Bernoulli scheme or Bernoulli shift is a generalization of the Bernoulli process to more than two possible outcomes. Bernoulli schemes are important in the study of dynamical systems, as most such systems exhibit a repellor that is the product of the Cantor set and a smooth...
- Bernoulli trialBernoulli trialIn the theory of probability and statistics, a Bernoulli trial is an experiment whose outcome is random and can be either of two possible outcomes, "success" and "failure"....
- Bernoulli map