A disphenoid is a polyhedron

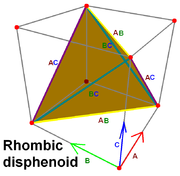
Polyhedron

In elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...

 whose four faces are identical triangles. The faces of a tetragonal disphenoid are isosceles; the faces of a rhombic disphenoid are scalene. If the faces are equilateral triangles, one obtains a regular tetrahedron, which is not normally considered a disphenoid.

All the solid angle

Solid angle

The solid angle, Ω, is the two-dimensional angle in three-dimensional space that an object subtends at a point. It is a measure of how large that object appears to an observer looking from that point...

s and vertex figure

Vertex figure

In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...

s of a disphenoid are the same. However, a disphenoid is not a regular polyhedron

Regular polyhedron

A regular polyhedron is a polyhedron whose faces are congruent regular polygons which are assembled in the same way around each vertex. A regular polyhedron is highly symmetrical, being all of edge-transitive, vertex-transitive and face-transitive - i.e. it is transitive on its flags...

, because its faces are not regular polygon

Regular polygon

A regular polygon is a polygon that is equiangular and equilateral . Regular polygons may be convex or star.-General properties:...

s.

Some tetragonal disphenoids will form honeycomb

Honeycomb (geometry)

In geometry, a honeycomb is a space filling or close packing of polyhedral or higher-dimensional cells, so that there are no gaps. It is an example of the more general mathematical tiling or tessellation in any number of dimensions....

s. The disphenoid whose four vertices are (-1, 0, 0), (1, 0, 0), (0, 1, 1), and (0, 1, -1) is such a disphenoid. Each of its four faces is an isosceles triangle with edges of lengths √3, √3, and 2. It can tesselate space to form the disphenoid tetrahedral honeycomb

Disphenoid tetrahedral honeycomb

The disphenoid tetrahedral honeycomb is a space-filling tessellation in Euclidean 3-space made up of identical nonregular tetrahedral cells....

. As Gibb describes, it can be folded without cutting or overlaps from a single sheet of a4 paper.

"Disphenoid" is also used to describe two forms of crystal

Crystal system

In crystallography, the terms crystal system, crystal family, and lattice system each refer to one of several classes of space groups, lattices, point groups, or crystals...

:

• A wedge-shaped crystal form of the tetragonal
  Tetragonal crystal system
  In crystallography, the tetragonal crystal system is one of the 7 lattice point groups. Tetragonal crystal lattices result from stretching a cubic lattice along one of its lattice vectors, so that the cube becomes a rectangular prism with a square base and height .There are two tetragonal Bravais...
  
   or orthorhombic system
  Orthorhombic crystal system
  In crystallography, the orthorhombic crystal system is one of the seven lattice point groups. Orthorhombic lattices result from stretching a cubic lattice along two of its orthogonal pairs by two different factors, resulting in a rectangular prism with a rectangular base and height , such that a,...
  
  . It has four triangular faces that are alike and that correspond in position to alternate faces of the tetragonal or orthorhombic dipyramid
  Bipyramid
  An n-gonal bipyramid or dipyramid is a polyhedron formed by joining an n-gonal pyramid and its mirror image base-to-base.The referenced n-gon in the name of the bipyramids is not an external face but an internal one, existing on the primary symmetry plane which connects the two pyramid halves.The...
  
  . It is symmetrical about each of three mutually perpendicular diad axes of symmetry in all classes except the tetragonal-disphenoidal, in which the form is generated by an inverse tetrad axis of symmetry.

• A crystal form bounded by eight scalene triangles arranged in pairs, constituting a tetragonal scalenohedron.

See also

• Snub disphenoid
  Snub disphenoid
  In geometry, the snub disphenoid is one of the Johnson solids . It is a three-dimensional solid that has only equilateral triangles as faces, and is therefore a deltahedron. It is not a regular polyhedron because some vertices have four faces and others have five...
  
   - A Johnson solid
  Johnson solid
  In geometry, a Johnson solid is a strictly convex polyhedron, each face of which is a regular polygon, but which is not uniform, i.e., not a Platonic solid, Archimedean solid, prism or antiprism. There is no requirement that each face must be the same polygon, or that the same polygons join around...
  
  with 12 equilateral triangle faces and D_2d symmetry.