Dolbeault cohomology
Encyclopedia
In mathematics
, in particular in algebraic geometry
and differential geometry, Dolbeault cohomology (named after Pierre Dolbeault
) is an analog of de Rham cohomology
for complex manifold
s. Let M be a complex manifold. Then the Dolbeault cohomology groups Hp,q(M,C) depend on a pair of integers p and q and are realized as a subquotient of the space of complex differential form
s of degree (p,q).
of complex differential forms of degree (p,q). In the article on complex forms
, the Dolbeault operator is defined as a differential operator on smooth sections
Since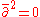
this operator has some associated cohomology
. Specifically, define the cohomology to be the quotient space
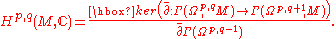
on a complex manifold X, then one can define likewise a fine resolution of the sheaf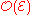
of holomorphic sections of E. This is therefore a recollection of the sheaf cohomology
of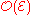
.
of the sheaf
of holomorphic differential forms. Specifically,
where Ωp is the sheaf of holomorphic p forms on M.
be the fine sheaf of 
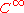forms of type 
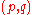. Then the 
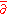-Poincare lemma says that the sequence
is exact. Like any long exact sequence, this sequence breaks up into short exact sequences. The long exact sequences of cohomology corresponding to these give the result, once one uses that the higher cohomologies of a fine sheaf vanish.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, in particular in algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
and differential geometry, Dolbeault cohomology (named after Pierre Dolbeault
Pierre Dolbeault
Pierre Dolbeault is a French mathematician.He studied with Henri Cartan and graduated in 1944 from the Ecole Normale Superieure. He taught in the 1950s in Montpellier and Bordeaux and later at the Universite Pierre et Marie Curie...
) is an analog of de Rham cohomology
De Rham cohomology
In mathematics, de Rham cohomology is a tool belonging both to algebraic topology and to differential topology, capable of expressing basic topological information about smooth manifolds in a form particularly adapted to computation and the concrete representation of cohomology classes...
for complex manifold
Complex manifold
In differential geometry, a complex manifold is a manifold with an atlas of charts to the open unit disk in Cn, such that the transition maps are holomorphic....
s. Let M be a complex manifold. Then the Dolbeault cohomology groups Hp,q(M,C) depend on a pair of integers p and q and are realized as a subquotient of the space of complex differential form
Complex differential form
In mathematics, a complex differential form is a differential form on a manifold which is permitted to have complex coefficients....
s of degree (p,q).
Construction of the cohomology groups
Let Ωp,q be the vector bundleVector bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
of complex differential forms of degree (p,q). In the article on complex forms
Complex differential form
In mathematics, a complex differential form is a differential form on a manifold which is permitted to have complex coefficients....
, the Dolbeault operator is defined as a differential operator on smooth sections
Since
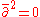
this operator has some associated cohomology
Cohomology
In mathematics, specifically in algebraic topology, cohomology is a general term for a sequence of abelian groups defined from a co-chain complex. That is, cohomology is defined as the abstract study of cochains, cocycles, and coboundaries...
. Specifically, define the cohomology to be the quotient space
Quotient space (linear algebra)
In linear algebra, the quotient of a vector space V by a subspace N is a vector space obtained by "collapsing" N to zero. The space obtained is called a quotient space and is denoted V/N ....
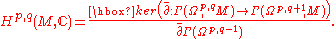
Dolbeault cohomology of vector bundles
If E is a holomorphic vector bundleHolomorphic vector bundle
In mathematics, a holomorphic vector bundle is a complex vector bundle over a complex manifold X such that the total space E is a complex manifold and the projection map \pi:E\to X is holomorphic. Fundamental examples are the holomorphic tangent bundle of a complex manifold, and its dual, the...
on a complex manifold X, then one can define likewise a fine resolution of the sheaf
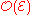of holomorphic sections of E. This is therefore a recollection of the sheaf cohomologySheaf cohomology
In mathematics, sheaf cohomology is the aspect of sheaf theory, concerned with sheaves of abelian groups, that applies homological algebra to make possible effective calculation of the global sections of a sheaf F...
of
.Dolbeault's theorem
Dolbeault's theorem is a complex analog of de Rham's theorem. It asserts that the Dolbeault cohomology is isomorphic to the sheaf cohomologySheaf cohomology
In mathematics, sheaf cohomology is the aspect of sheaf theory, concerned with sheaves of abelian groups, that applies homological algebra to make possible effective calculation of the global sections of a sheaf F...
of the sheaf
Sheaf (mathematics)
In mathematics, a sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space. The data can be restricted to smaller open sets, and the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of...
of holomorphic differential forms. Specifically,
where Ωp is the sheaf of holomorphic p forms on M.
Proof
Let be the fine sheaf of forms of type 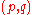. Then the 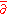-Poincare lemma says that the sequenceis exact. Like any long exact sequence, this sequence breaks up into short exact sequences. The long exact sequences of cohomology corresponding to these give the result, once one uses that the higher cohomologies of a fine sheaf vanish.