Curry–Howard - AbsoluteAstronomy.com

Programming language theory

Programming language theory is a branch of computer science that deals with the design, implementation, analysis, characterization, and classification of programming languages and their individual features. It falls within the discipline of computer science, both depending on and affecting...

and proof theory

Proof theory

Proof theory is a branch of mathematical logic that represents proofs as formal mathematical objects, facilitating their analysis by mathematical techniques. Proofs are typically presented as inductively-defined data structures such as plain lists, boxed lists, or trees, which are constructed...

, the Curry–Howard correspondence (also known as the Curry–Howard isomorphism or equivalence, or the proofs-as-programs and propositions- or formulae-as-types correspondence) is the direct relationship between computer programs and proofs. It is a generalization of a syntactic analogy

Analogy

Analogy is a cognitive process of transferring information or meaning from a particular subject to another particular subject , and a linguistic expression corresponding to such a process...

between systems of formal logic and computational calculi that was first discovered by the American mathematician

Mathematician

A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....

Haskell Curry

Haskell Brooks Curry was an American mathematician and logician. Curry is best known for his work in combinatory logic; while the initial concept of combinatory logic was based on a single paper by Moses Schönfinkel, much of the development was done by Curry. Curry is also known for Curry's...

and logician William Alvin Howard

William Alvin Howard

William Alvin Howard is a proof theorist best known for his work demonstrating formal similarity between intuitionistic logic and the simply typed lambda calculus that has come to be known as the Curry–Howard correspondence. He has also been active in the theory of proof-theoretic ordinals. He...

Origin, scope, and consequences

At the very beginning, the Curry–Howard correspondence is

the observation in 1934 by Curry
Haskell Curry
Haskell Brooks Curry was an American mathematician and logician. Curry is best known for his work in combinatory logic; while the initial concept of combinatory logic was based on a single paper by Moses Schönfinkel, much of the development was done by Curry. Curry is also known for Curry's...

that the type
Typed lambda calculus
A typed lambda calculus is a typed formalism that uses the lambda-symbol to denote anonymous function abstraction. In this context, types are usually objects of a syntactic nature that are assigned to lambda terms; the exact nature of a type depends on the calculus considered...

s of the combinators could be seen as axiom-schemes for intuitionistic
Intuitionism
In the philosophy of mathematics, intuitionism, or neointuitionism , is an approach to mathematics as the constructive mental activity of humans. That is, mathematics does not consist of analytic activities wherein deep properties of existence are revealed and applied...

implicational logic,
the observation in 1958 by Curry that a certain kind of proof system
Proof calculus
In mathematical logic, a proof calculus corresponds to a family of formal systems that use a common style of formal inference for its inference rules...

, referred to as Hilbert-style deduction system
Hilbert-style deduction system
In logic, especially mathematical logic, a Hilbert system, sometimes called Hilbert calculus or Hilbert–Ackermann system, is a type of system of formal deduction attributed to Gottlob Frege and David Hilbert...

s, coincides on some fragment to the typed fragment of a standard model of computation
Model of computation
In computability theory and computational complexity theory, a model of computation is the definition of the set of allowable operations used in computation and their respective costs...

known as combinatory logic
Combinatory logic
Combinatory logic is a notation introduced by Moses Schönfinkel and Haskell Curry to eliminate the need for variables in mathematical logic. It has more recently been used in computer science as a theoretical model of computation and also as a basis for the design of functional programming...

,
the observation in 1969 by Howard
William Alvin Howard
William Alvin Howard is a proof theorist best known for his work demonstrating formal similarity between intuitionistic logic and the simply typed lambda calculus that has come to be known as the Curry–Howard correspondence. He has also been active in the theory of proof-theoretic ordinals. He...

that another, more "high-level" proof system
Proof calculus
In mathematical logic, a proof calculus corresponds to a family of formal systems that use a common style of formal inference for its inference rules...

, referred to as natural deduction
Natural deduction
In logic and proof theory, natural deduction is a kind of proof calculus in which logical reasoning is expressed by inference rules closely related to the "natural" way of reasoning...

, can be directly interpreted in its intuitionistic version as a typed variant of the model of computation
Model of computation
In computability theory and computational complexity theory, a model of computation is the definition of the set of allowable operations used in computation and their respective costs...

known as lambda calculus
Lambda calculus
In mathematical logic and computer science, lambda calculus, also written as λ-calculus, is a formal system for function definition, function application and recursion. The portion of lambda calculus relevant to computation is now called the untyped lambda calculus...

.

In other words, the Curry–Howard correspondence is the observation that two families of formalisms which had seemed unrelated—namely, the proof systems on one hand, and the models of computation on the other—were, in the two examples considered by Curry and Howard, in fact structurally the same kind of objects.

If one now abstracts on the peculiarities of this or that formalism, the immediate generalization is the following claim: a proof is a program, the formula it proves is a type for the program. Most informally, this can be seen as an analogy

Analogy

Analogy is a cognitive process of transferring information or meaning from a particular subject to another particular subject , and a linguistic expression corresponding to such a process...

that states that the return type

Return type

In computer programming, the return type defines and constrains the data type of value returned from a method or function...

of a function (i.e., the type of values returned by a function) is analogous to a logical theorem, subject to hypotheses corresponding to the types of the argument values passed to the function; and that the program to compute that function is analogous to a proof of that theorem. This sets a form of logic programming

Logic programming

Logic programming is, in its broadest sense, the use of mathematical logic for computer programming. In this view of logic programming, which can be traced at least as far back as John McCarthy's [1958] advice-taker proposal, logic is used as a purely declarative representation language, and a...

on a rigorous foundation: proofs can be represented as programs, and especially as lambda terms, or proofs can be run.

The correspondence has been the starting point of a large spectrum of new research after its discovery, leading in particular to a new class of formal system

Formal system

In formal logic, a formal system consists of a formal language and a set of inference rules, used to derive an expression from one or more other premises that are antecedently supposed or derived . The axioms and rules may be called a deductive apparatus...

s designed to act both as a proof system

Proof calculus

In mathematical logic, a proof calculus corresponds to a family of formal systems that use a common style of formal inference for its inference rules...

and as a typed functional programming language. This includes Martin-Löf's intuitionistic type theory

Intuitionistic type theory

Intuitionistic type theory, or constructive type theory, or Martin-Löf type theory or just Type Theory is a logical system and a set theory based on the principles of mathematical constructivism. Intuitionistic type theory was introduced by Per Martin-Löf, a Swedish mathematician and philosopher,...

and Coquand's Calculus of Constructions

Calculus of constructions

The calculus of constructions is a formal language in which both computer programs and mathematical proofs can be expressed. This language forms the basis of theory behind the Coq proof assistant, which implements the derivative calculus of inductive constructions.-General traits:The CoC is a...

, two calculi in which proofs are regular objects of the discourse and in which one can state properties of proofs the same way as of any program. This field of research is usually referred to as modern type theory

Type theory

In mathematics, logic and computer science, type theory is any of several formal systems that can serve as alternatives to naive set theory, or the study of such formalisms in general...

.

Such typed lambda calculi

Typed lambda calculus

A typed lambda calculus is a typed formalism that uses the lambda-symbol to denote anonymous function abstraction. In this context, types are usually objects of a syntactic nature that are assigned to lambda terms; the exact nature of a type depends on the calculus considered...

derived from the Curry–Howard paradigm led to software like Coq

Coq

In computer science, Coq is an interactive theorem prover. It allows the expression of mathematical assertions, mechanically checks proofs of these assertions, helps to find formal proofs, and extracts a certified program from the constructive proof of its formal specification...

in which proofs seen as programs can be formalized, checked, and run.

A converse direction is to use a program to extract a proof, given its correctness— an area of research which is closely related to proof-carrying code

Proof-Carrying Code

Proof-carrying code is a software mechanism that allows a host system to verify properties about an application via a formal proof that accompanies the application's executable code. The host system can quickly verify the validity of the proof, and it can compare the conclusions of the proof to...

. This is only feasible if the programming language

Programming language

A programming language is an artificial language designed to communicate instructions to a machine, particularly a computer. Programming languages can be used to create programs that control the behavior of a machine and/or to express algorithms precisely....

the program is written for is very richly typed: the development of such type systems has been partly motivated by the wish to make the Curry–Howard correspondence practically relevant.

The Curry–Howard correspondence also raised new questions regarding the computational content of proof concepts which were not covered by the original works of Curry and Howard. In particular, classical logic

Classical logic

Classical logic identifies a class of formal logics that have been most intensively studied and most widely used. The class is sometimes called standard logic as well...

has been shown to correspond to the ability to manipulate the continuation

Continuation

In computer science and programming, a continuation is an abstract representation of the control state of a computer program. A continuation reifies the program control state, i.e...

of programs and the symmetry of sequent calculus

Sequent calculus

In proof theory and mathematical logic, sequent calculus is a family of formal systems sharing a certain style of inference and certain formal properties. The first sequent calculi, systems LK and LJ, were introduced by Gerhard Gentzen in 1934 as a tool for studying natural deduction in...

to express the duality between the two evaluation strategies

Evaluation strategy

In computer science, an evaluation strategy is a set of rules for evaluating expressions in a programming language. Emphasis is typically placed on functions or operators: an evaluation strategy defines when and in what order the arguments to a function are evaluated, when they are substituted...

known as call-by-name and call-by-value.

Speculatively, the Curry–Howard correspondence might be expected to lead to a substantial unification

Unifying theories in mathematics

There have been several attempts in history to reach a unified theory of mathematics. Some of the greatest mathematicians have expressed views that the whole subject should be fitted into one theory.-Historical perspective:...

between mathematical logic and foundational computer science:

Hilbert-style logic and natural deduction are but two kinds of proof systems among a large family of formalisms. Alternative syntaxes include sequent calculus

Sequent calculus

, proof net

Proof net

In proof theory, proof nets are a geometrical method of representing proofs thateliminates two forms of bureaucracy that differentiates proofs: irrelevant syntactical features of regular proof calculi such as the natural deduction calculus and the sequent calculus, and the order of rules applied...

s, calculus of structures

Calculus of structures

The calculus of structures is a proof calculus with deep inference for studying the structural proof theory of noncommutative logic. The calculus has since been applied to study linear logic, classical logic, modal logic, and process calculi, and many benefits are claimed to follow in these...

, etc. If one admits the Curry–Howard correspondence as the general principle that any proof system hides a model of computation, a theory of the underlying untyped computational structure of these kinds of proof system should be possible. Then, a natural question is whether something mathematically interesting can be said about these underlying computational calculi.

Conversely, combinatory logic

Combinatory logic

Combinatory logic is a notation introduced by Moses Schönfinkel and Haskell Curry to eliminate the need for variables in mathematical logic. It has more recently been used in computer science as a theoretical model of computation and also as a basis for the design of functional programming...

and simply-typed lambda calculus

Simply typed lambda calculus

The simply typed lambda calculus , a formof type theory, is a typed interpretation of the lambda calculus with only one type constructor: \to that builds function types. It is the canonical and simplest example of a typed lambda calculus...

are not the only models of computation, either. Girard's linear logic

Linear logic

Linear logic is a substructural logic proposed by Jean-Yves Girard as a refinement of classical and intuitionistic logic, joining the dualities of the former with many of the constructive properties of the latter...

was developed from the fine analysis of the use of resources in some models of lambda calculus; can we imagine a typed version of Turing's machine

Turing machine

A Turing machine is a theoretical device that manipulates symbols on a strip of tape according to a table of rules. Despite its simplicity, a Turing machine can be adapted to simulate the logic of any computer algorithm, and is particularly useful in explaining the functions of a CPU inside a...

that would behave as a proof system? Typed assembly language

Typed Assembly Language

In computer science, a typed assembly language is an assembly language that is extended to include a method of annotating the datatype of each value that is manipulated by the code. These annotations can then be used by a program that processes the assembly language code in order to analyse how...

s are such an instance of "low-level" models of computation that carry types.

Because of the possibility of writing non-terminating programs, Turing-complete models of computation (such as languages with arbitrary recursive functions

Recursion (computer science)

Recursion in computer science is a method where the solution to a problem depends on solutions to smaller instances of the same problem. The approach can be applied to many types of problems, and is one of the central ideas of computer science....

) must be interpreted with care, as naive application of the correspondence leads to an inconsistent logic. The best way of dealing with arbitrary computation from a logical point of view is still an actively-debated research question, but one popular approach is based on using monads to segregate provably terminating from potentially non-terminating code (an approach which also generalizes to much richer models of computation, and is itself related to modal logic by a natural extension of the Curry–Howard isomorphism). A more radical approach, advocated by total functional programming

Total functional programming

Total functional programming is a programming paradigm that restricts the range of programs to those that are provably terminating....

, is to eliminate unrestricted recursion (and forgo Turing-completeness, although still retaining high computational complexity), using more controlled corecursion

Corecursion

In computer science, corecursion is a type of operation that is dual to recursion. Corecursion and codata allow total languages to work with infinite data structures such as streams. Corecursion is often used in conjunction with lazy evaluation. Corecursion can produce both finite and infinite data...

where non-terminating behavior is actually desired.

General formulation

In its more general formulation, the Curry–Howard correspondence is a correspondence between formal proof calculi

Proof calculus

In mathematical logic, a proof calculus corresponds to a family of formal systems that use a common style of formal inference for its inference rules...

and type systems for models of computation

Model of computation

In computability theory and computational complexity theory, a model of computation is the definition of the set of allowable operations used in computation and their respective costs...

. In particular, it splits into two correspondences. One at the level of formulas and types

Data type

In computer programming, a data type is a classification identifying one of various types of data, such as floating-point, integer, or Boolean, that determines the possible values for that type; the operations that can be done on values of that type; the meaning of the data; and the way values of...

that is independent of which particular proof system or model of computation is considered, and one at the level of proofs

Mathematical proof

In mathematics, a proof is a convincing demonstration that some mathematical statement is necessarily true. Proofs are obtained from deductive reasoning, rather than from inductive or empirical arguments. That is, a proof must demonstrate that a statement is true in all cases, without a single...

and programs

Computer program

A computer program is a sequence of instructions written to perform a specified task with a computer. A computer requires programs to function, typically executing the program's instructions in a central processor. The program has an executable form that the computer can use directly to execute...

which, this time, is specific to the particular choice of proof system and model of computation considered.

At the level of formulas and types, the correspondence says that implication behaves the same as a function type, conjunction as a "product" type (this may be called a tuple, a struct, a list, or some other term depending on the language), disjunction as a sum type (this type may be called a union), the false formula as the empty type and the true formula as the singleton type (whose sole member is the null object). Quantifiers correspond to dependent

Dependent type

In computer science and logic, a dependent type is a type that depends on a value. Dependent types play a central role in intuitionistic type theory and in the design of functional programming languages like ATS, Agda and Epigram....

products or sums (as appropriate). This is summarized in the following table:

Logic side	Programming side
universal quantification Universal quantification In predicate logic, universal quantification formalizes the notion that something is true for everything, or every relevant thing....	dependent product type Dependent type In computer science and logic, a dependent type is a type that depends on a value. Dependent types play a central role in intuitionistic type theory and in the design of functional programming languages like ATS, Agda and Epigram....
existential quantification Existential quantification In predicate logic, an existential quantification is the predication of a property or relation to at least one member of the domain. It is denoted by the logical operator symbol ∃ , which is called the existential quantifier...	dependent sum type
implication	function type Function type In computer science, a function type is the type of a variable or parameter to which a function has or can be assigned or the result type of a higher-order function returning a function....
conjunction Logical conjunction In logic and mathematics, a two-place logical operator and, also known as logical conjunction, results in true if both of its operands are true, otherwise the value of false....	product type Product type In programming languages and type theory, a product of types is another, compounded, type in a structure. The "operands" of the product are types, and the structure of a product type is determined by the fixed order of the operands in the product. An instance of a product type retains the fixed...
disjunction Logical disjunction In logic and mathematics, a two-place logical connective or, is a logical disjunction, also known as inclusive disjunction or alternation, that results in true whenever one or more of its operands are true. E.g. in this context, "A or B" is true if A is true, or if B is true, or if both A and B are...	sum type
true formula	unit type Unit type In the area of mathematical logic, and computer science known as type theory, a unit type is a type that allows only one value . The carrier associated with a unit type can be any singleton set. There is an isomorphism between any two such sets, so it is customary to talk about the unit type and...
false formula	bottom type Bottom type In type theory, a theory within mathematical logic, the bottom type is the type that has no values. It is also called the zero or empty type, and is sometimes denoted with falsum .A function whose return type is bottom cannot return any value...

At the level of proof systems and models of computations, the correspondence mainly shows the identity of structure, first, between some particular formulations of systems known as Hilbert-style deduction system

Hilbert-style deduction system

In logic, especially mathematical logic, a Hilbert system, sometimes called Hilbert calculus or Hilbert–Ackermann system, is a type of system of formal deduction attributed to Gottlob Frege and David Hilbert...

and combinatory logic

Combinatory logic

, and, secondly, between some particular formulations of systems known as natural deduction

Natural deduction

In logic and proof theory, natural deduction is a kind of proof calculus in which logical reasoning is expressed by inference rules closely related to the "natural" way of reasoning...

and lambda calculus

Lambda calculus

In mathematical logic and computer science, lambda calculus, also written as λ-calculus, is a formal system for function definition, function application and recursion. The portion of lambda calculus relevant to computation is now called the untyped lambda calculus...

Logic side	Programming side
Hilbert-style deduction system Hilbert-style deduction system In logic, especially mathematical logic, a Hilbert system, sometimes called Hilbert calculus or Hilbert–Ackermann system, is a type of system of formal deduction attributed to Gottlob Frege and David Hilbert...	type system for combinatory logic Combinatory logic Combinatory logic is a notation introduced by Moses Schönfinkel and Haskell Curry to eliminate the need for variables in mathematical logic. It has more recently been used in computer science as a theoretical model of computation and also as a basis for the design of functional programming...
natural deduction Natural deduction In logic and proof theory, natural deduction is a kind of proof calculus in which logical reasoning is expressed by inference rules closely related to the "natural" way of reasoning...	type system for lambda calculus Lambda calculus In mathematical logic and computer science, lambda calculus, also written as λ-calculus, is a formal system for function definition, function application and recursion. The portion of lambda calculus relevant to computation is now called the untyped lambda calculus...

Between the natural deduction system and the lambda calculus there there are the following correspondences:

Logic side	Programming side
hypotheses	free variables
implication elimination (modus ponens)	application
implication introduction	abstraction

Correspondence between Hilbert-style deduction systems and combinatory logic

It was at the beginning a simple remark in Curry and Feys's 1958 book on combinatory logic: the simplest types for the basic combinators K and S of combinatory logic

Combinatory logic

surprisingly corresponded to the respective axiom schemes α → (β → α) and (α → (β → γ)) → ((α → β) → (α → γ)) used in Hilbert-style deduction system

Hilbert-style deduction system

s. For this reason, these schemes are now often called axioms K and S. Examples of programs seen as proofs in a Hilbert-style logic are given below.

If one restricts to the implicational intuitionistic fragment, a simple way to formalize logic in Hilbert's style is as follows. Let Γ be a finite collection of formulas, considered as hypotheses. We say that δ is derivable from Γ, and we write Γ δ, in the following cases:

δ is an hypothesis, i.e. it is a formula of Γ,
δ is an instance of an axiom scheme; i.e., under the most common axiom system:
- δ has the form α → (β → α), or
- δ has the form (α → (β → γ)) → ((α → β) → (α → γ)),
δ follows by deduction, i.e., for some α, both α → δ and α are already derivable from Γ (this is the rule of modus ponens
Modus ponens
In classical logic, modus ponendo ponens or implication elimination is a valid, simple argument form. It is related to another valid form of argument, modus tollens. Both Modus Ponens and Modus Tollens can be mistakenly used when proving arguments...

)

This can be formalized using inference rules, what we do in the left column of the following table.

We can formulate typed combinatory logic using a similar syntax: let Γ be a finite collection of variables, annotated with their types. A term T (also annotated with its type) will depend on these variables [Γ T:δ] when:

T is one of the variables in Γ,
T is a basic combinator; i.e., under the most common combinator basis:
- T is K:α → (β → α) [where α and β denote the types of its arguments], or
- T is S:(α → (β → γ)) → ((α → β) → (α → γ)),
T is the composition of two subterms which depend on the variables in Γ.

The generation rules defined here are given in the right-column below. Curry's remark simply states that both columns are in one-to-one correspondence. The restriction of the correspondence to intuitionistic logic

Intuitionistic logic

Intuitionistic logic, or constructive logic, is a symbolic logic system differing from classical logic in its definition of the meaning of a statement being true. In classical logic, all well-formed statements are assumed to be either true or false, even if we do not have a proof of either...

means that some classical

Classical logic

Classical logic identifies a class of formal logics that have been most intensively studied and most widely used. The class is sometimes called standard logic as well...

tautologies

Tautology (logic)

In logic, a tautology is a formula which is true in every possible interpretation. Philosopher Ludwig Wittgenstein first applied the term to redundancies of propositional logic in 1921; it had been used earlier to refer to rhetorical tautologies, and continues to be used in that alternate sense...

, such as Peirce's law

Peirce's law

In logic, Peirce's law is named after the philosopher and logician Charles Sanders Peirce. It was taken as an axiom in his first axiomatisation of propositional logic. It can be thought of as the law of excluded middle written in a form that involves only one sort of connective, namely...

((α → β) → α) → α, are excluded from the correspondence.

Hilbert-style intuitionistic implicational logic	Simply-typed combinatory logic

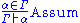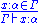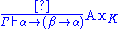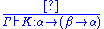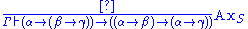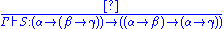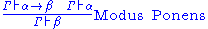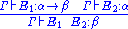Seen at a more abstract level, the correspondence can be restated as shown in the following table. Especially, the deduction theorem

Deduction theorem

In mathematical logic, the deduction theorem is a metatheorem of first-order logic. It is a formalization of the common proof technique in which an implication A → B is proved by assuming A and then proving B from this assumption. The deduction theorem explains why proofs of conditional...

specific to Hilbert-style logic matches the process of abstraction elimination of combinatory logic.

Logic side	Programming side
assumption	variable
axioms	combinators
modus ponens	application
deduction theorem Deduction theorem In mathematical logic, the deduction theorem is a metatheorem of first-order logic. It is a formalization of the common proof technique in which an implication A → B is proved by assuming A and then proving B from this assumption. The deduction theorem explains why proofs of conditional...	abstraction elimination

Thanks to the correspondence, results from combinatory logic can be transferred to Hilbert-style logic and vice-versa. For instance, the notion of reduction of terms in combinatory logic can be transferred to Hilbert-style logic and it provides a way to canonically transform proofs into other proofs of the same statement. One can also transfer the notion of normal terms to a notion of normal proofs, expressing that the hypotheses of the axioms never need to be all detached (since otherwise a simplification can happen).

Conversely, the non provability in intuitionistic logic of Peirce's law

Peirce's law

can be transferred back to combinatory logic: there is no typed term of combinatory logic that is typable with type ((α → β) → α) → α.

Results on the completeness of some sets of combinators or axioms can also be transferred. For instance, the fact that the combinator X constitutes a one-point basis of (extensional) combinatory logic implies that the single axiom scheme) → ((α → β) → (α → γ))) → ((δ → (ε → δ)) → ζ)) → ζ,
which is the principal type

Principal type

In type theory, the principal type of an expression is the most general possible type given an expression. One way to compute the principal type of an expression is by deploying Robinson's unification algorithm, which is used by the Hindley–Milner type inference algorithm.Expressions always...

of X, is an adequate replacement to the combination of the axiom schemes

α → (β → α) and) → ((α → β) → (α → γ)).

Correspondence between natural deduction and lambda calculus

After Curry

Haskell Curry

emphasized the syntactic correspondence between Hilbert-style deduction

Hilbert-style deduction system

and combinatory logic

Combinatory logic

, Howard

William Alvin Howard

made explicit in 1969 a syntactic analogy between the programs of simply-typed lambda calculus

Simply typed lambda calculus

and the proofs of natural deduction

Natural deduction

In logic and proof theory, natural deduction is a kind of proof calculus in which logical reasoning is expressed by inference rules closely related to the "natural" way of reasoning...

. Below, the left-hand side formalizes intuitionistic implicational natural deduction as a calculus of sequent

Sequent

In proof theory, a sequent is a formalized statement of provability that is frequently used when specifying calculi for deduction. In the sequent calculus, the name sequent is used for the construct which can be regarded as a specific kind of judgment, characteristic to this deduction system.-...

s (the use of sequents is standard in discussions of the Curry-Howard isomorphism as it allows the deduction rules to be stated more cleanly) with implicit weakening and the right-hand side shows the typing rules of lambda calculus

Lambda calculus

. In the left-hand side, Γ, Γ₁ and Γ₂ denote ordered sequences of formulas while in the right-hand side, they denote sequences of named formulas with all names different.

Intuitionistic implicational natural deduction	Lambda calculus type assignment rules

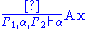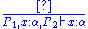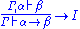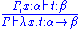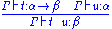To paraphrase the correspondence, proving Γ α means having a program that, given values with the types listed in Γ, manufactures an object of type α. An axiom corresponds to the introduction of a new variable with a new, unconstrained type, the → I rule corresponds to function abstraction and the → E rule corresponds to function application. Observe that the correspondence is not exact if the context Γ is taken to be a set of formulas as, e.g., the λ-terms λx.λy.x and λx.λy.y of type α → α → α would not be distinguished in the correspondence. Examples are given below.

Howard showed that the correspondence extends to other connectives of the logic and other constructions of simply-typed lambda calculus. Seen at an abstract level, the correspondence can then be summarized as shown in the following table. Especially, it also shows that the notion of normal forms in lambda calculus

Lambda calculus

matches Prawitz

Dag Prawitz

Dag Prawitz is a Swedish philosopher and logician. He is best known for his work on proof theory and the foundations of natural deduction....

's notion of normal deduction in natural deduction

Natural deduction

In logic and proof theory, natural deduction is a kind of proof calculus in which logical reasoning is expressed by inference rules closely related to the "natural" way of reasoning...

, from what we deduce, among others, that the algorithms for the type inhabitation problem

Type inhabitation problem

In type theory, a branch of mathematical logic, in a given typed calculus, the type inhabitation problem for this calculus is the following problem: given a type \tau and a type environment \Gamma, does there exist a \lambda-term M such that \Gamma \vdash M : \tau? With an empty type environment,...

can be turned into algorithms for deciding intuitionistic provability.

Logic side	Programming side
axiom	variable
introduction rule	constructor
elimination rule	destructor
normal deduction	normal form
normalisation of deductions	weak normalisation Normalization property (lambda-calculus) In mathematical logic and theoretical computer science, a rewrite system has the strong normalization property if every term is strongly normalizing; that is, if every sequence of rewrites eventually terminates to a term in normal form...
provability	type inhabitation problem Type inhabitation problem In type theory, a branch of mathematical logic, in a given typed calculus, the type inhabitation problem for this calculus is the following problem: given a type \tau and a type environment \Gamma, does there exist a \lambda-term M such that \Gamma \vdash M : \tau? With an empty type environment,...
intuitionistic tautology	inhabited type

Howard's correspondence naturally extends to other extensions of natural deduction

Natural deduction

In logic and proof theory, natural deduction is a kind of proof calculus in which logical reasoning is expressed by inference rules closely related to the "natural" way of reasoning...

and simply-typed lambda calculus

Simply typed lambda calculus

. Here is a non exhaustive list:

Girard-Reynolds System F
System F
System F, also known as the polymorphic lambda calculus or the second-order lambda calculus, is a typed lambda calculus that differs from the simply typed lambda calculus by the introduction of a mechanism of universal quantification over types...

as a common language for both second-order propositional logic and polymorphic lambda calculus,
higher-order logic
Higher-order logic
In mathematics and logic, a higher-order logic is a form of predicate logic that is distinguished from first-order logic by additional quantifiers and a stronger semantics...

and Girard's System F_ω
System F
System F, also known as the polymorphic lambda calculus or the second-order lambda calculus, is a typed lambda calculus that differs from the simply typed lambda calculus by the introduction of a mechanism of universal quantification over types...
inductive types as algebraic data type
Algebraic data type
In computer programming, particularly functional programming and type theory, an algebraic data type is a datatype each of whose values is data from other datatypes wrapped in one of the constructors of the datatype. Any wrapped datum is an argument to the constructor...
necessity in modal logic
Modal logic
Modal logic is a type of formal logic that extends classical propositional and predicate logic to include operators expressing modality. Modals — words that express modalities — qualify a statement. For example, the statement "John is happy" might be qualified by saying that John is...

and staged computation
possibility in modal logic
Modal logic
Modal logic is a type of formal logic that extends classical propositional and predicate logic to include operators expressing modality. Modals — words that express modalities — qualify a statement. For example, the statement "John is happy" might be qualified by saying that John is...

and monadic types for effects
The λ_I calculus corresponds to relevant logic.
The local truth (∇) modality in Grothendieck topology
Grothendieck topology
In category theory, a branch of mathematics, a Grothendieck topology is a structure on a category C which makes the objects of C act like the open sets of a topological space. A category together with a choice of Grothendieck topology is called a site.Grothendieck topologies axiomatize the notion...

or the equivalent "lax" modality (∘) of Benton, Bierman, and de Paiva (1998) correspond to CL-logic describing "computation types"
...

Correspondence between classical logic and control operators

At the time of Curry, and also at the time of Howard, the proof-as-program correspondence concerned only intuitionistic logic

Intuitionistic logic

, i.e. a logic in which, in particular, Peirce's law

Peirce's law

was not deducible. The extension of the correspondence to Peirce's law and hence to classical logic

Classical logic

Classical logic identifies a class of formal logics that have been most intensively studied and most widely used. The class is sometimes called standard logic as well...

became clear from the work of Griffin on typing operators that capture the evaluation context of a given program execution so that this evaluation context can be later on reinstalled. The basic Curry–Howard-style correspondence for classical logic is given below. Note the correspondence between the double-negation translation used to map classical proofs to intuitionistic logic and the continuation-passing-style

Continuation-passing style

In functional programming, continuation-passing style is a style of programming in which control is passed explicitly in the form of a continuation. Gerald Jay Sussman and Guy L. Steele, Jr...

translation used to map lambda terms involving control to pure lambda terms. More particularly, call-by-name continuation-passing-style translations relates to Kolmogorov's double negation translation and call-by-value continuation-passing-style translations relates to a kind of double-negation translation due to Kuroda.

Logic side	Programming side
Peirce's law Peirce's law In logic, Peirce's law is named after the philosopher and logician Charles Sanders Peirce. It was taken as an axiom in his first axiomatisation of propositional logic. It can be thought of as the law of excluded middle written in a form that involves only one sort of connective, namely... : ((α → β) → α) → α	call-with-current-continuation Call-with-current-continuation In functional programming, the function call-with-current-continuation, commonly abbreviated call/cc, is a control operator that originated in its current form in the Scheme programming language and now exists in several other programming languages....
double-negation translation	continuation-passing-style translation Continuation-passing style In functional programming, continuation-passing style is a style of programming in which control is passed explicitly in the form of a continuation. Gerald Jay Sussman and Guy L. Steele, Jr...

A finer Curry–Howard correspondence exists for classical logic if one defines classical logic not by adding an axiom such as Peirce's law

Peirce's law

, but by allowing several conclusions in sequents. In the case of classical natural deduction, there exists a proofs-as-programs correspondence with the typed programs of Parigot's λμ-calculus

Lambda-mu calculus

In mathematical logic and computer science, the lambda-mu calculus is an extension of the lambda calculus, and was introduced by M. Parigot. It introduces two new operators: the mu operator and the bracket operator...

Sequent calculus

A proofs-as-programs correspondence can be settled for the formalism known as Gentzen's sequent calculus

Sequent calculus

but it is not a correspondence with a well-defined pre-existing model of computation as it was for Hilbert-style and natural deductions.

Sequent calculus is characterized by the presence of left introduction rules, right introduction rule and a cut rule that can be eliminated. The structure of sequent calculus relates to a calculus whose structure is close to the one of some abstract machine

Abstract machine

An abstract machine, also called an abstract computer, is a theoretical model of a computer hardware or software system used in automata theory...

s. The informal correspondence is as follows:

Logic side	Programming side
cut elimination	reduction in a form of abstract machine
right introduction rules	constructors of code
left introduction rules	constructors of evaluation stacks
priority to right-hand side in cut-elimination	call-by-name reduction
priority to left-hand side in cut-elimination	call-by-value reduction

The role of de Bruijn

N. G. de Bruijn

Nicolaas Govert de Bruijn

Nicolaas Govert de Bruijn is a Dutch mathematician, affiliated as professor emeritus with the Eindhoven University of Technology. He received his Ph.D. in 1943 from Vrije Universiteit Amsterdam....

used the lambda notation for representing proofs of the theorem checker Automath, and represented propositions as "categories" of their proofs. It was in the late 1960s at the same period of time Howard wrote his manuscript; de Bruijn was likely unaware of Howard's work, and stated the correspondence independently (Sørensen & Urzyczyn [1998] 2006, pp 98–99). Some researchers tend to use the term Curry–Howard–de Bruijn correspondence in place of Curry–Howard correspondence.

BHK interpretation

The BHK interpretation

BHK interpretation

In mathematical logic, the Brouwer–Heyting–Kolmogorov interpretation, or BHK interpretation, of intuitionistic logic was proposed by L. E. J. Brouwer, Arend Heyting and independently by Andrey Kolmogorov...

interprets intuitionistic proofs as functions but it does not specify the class of functions relevant for the interpretation. If one takes lambda calculus for this class of function, then the BHK interpretation

BHK interpretation

tells the same as Howard's correspondence between natural deduction and lambda calculus.

Realizability

Kleene

Stephen Cole Kleene

Stephen Cole Kleene was an American mathematician who helped lay the foundations for theoretical computer science...

's recursive realizability

Realizability

Realizability is a part of proof theory which can be used to handle information about formulas instead of about the proofs of formulas. A natural number n is said to realize a statement in the language of arithmetic of natural numbers...

splits proofs of intuitionistic arithmetic into the pair of a recursive function and of
a proof of a formula expressing that the recursive function "realizes", i.e. correctly instantiates the disjunctions and existential quantifiers of the initial formula so that the formula gets true.

Kreisel

Georg Kreisel

Georg Kreisel FRS is an Austrian-born mathematical logician who has studied and worked in Great Britain and America. Kreisel came from a Jewish background; his family sent him to England before the Anschluss, where he studied mathematics at Trinity College, Cambridge and then, during World War...

's modified realizability applies to intuitionistic higher-order predicate logic and shows that the simply-typed lambda term

Simply typed lambda calculus

inductively extracted from the proof realizes the initial formula. In the case of propositional logic, it coincides with Howard's statement: the extracted lambda term is the proof itself (seen as an untyped lambda term) and the realizability statement is a paraphrase of the fact that the extracted lambda term has the type that the formula means (seen as a type).

Gödel

Kurt Gödel

Kurt Friedrich Gödel was an Austrian logician, mathematician and philosopher. Later in his life he emigrated to the United States to escape the effects of World War II. One of the most significant logicians of all time, Gödel made an immense impact upon scientific and philosophical thinking in the...

's dialectica interpretation

Dialectica interpretation

In proof theory, the Dialectica interpretation is a proof interpretation of intuitionistic arithmetic into a finite type extension of primitive recursive arithmetic, the so-called System T. It was developed by Kurt Gödel to provide a consistency proof of arithmetic...

realizes (an extension of) intuitionistic arithmetic with computable functions. The connection with lambda calculus is unclear, even in the case of natural deduction.

Curry–Howard–Lambek correspondence

Joachim Lambek

Joachim Lambek is Peter Redpath Emeritus Professor of Pure Mathematics at McGill University, where he earned his Ph.D. degree in 1950 with Hans Julius Zassenhaus as advisor. He is called Jim by his friends.- Scholarly work :...

showed in the early 1970s that the proofs of intuitionistic propositional logic and the combinators of typed combinatory logic

Combinatory logic

share a common equational theory which is the one of cartesian closed categories. The expression Curry–Howard–Lambek correspondence is now used by some people to refer to the three way isomorphism between intuitionistic logic, typed lambda calculus and cartesian closed categories, with objects being interpreted as types or propositions and morphisms as terms or proofs. The correspondence works at the equational level and is not the expression of a syntactic identity of structures as it is the case for each of Curry's and Howard's correspondences: i.e. the structure of a well-defined morphism in a cartesian-closed category is not comparable to the structure of a proof of the corresponding judgment in either Hilbert-style logic or natural deduction. To clarify this distinction, the underlying syntactic structure of cartesian closed categories is rephrased below.

Objects (types) are defined by

is an object
if and are objects then 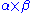and are objects.

Morphisms (terms) are defined by

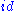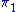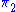, , , and are morphisms
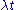if is a morphism, is a morphism
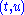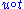if and are morphisms, and are morphisms.

Well-defined morphisms (typed terms) are defined by the following (typing) rules (in which the usual categorical morphism notation

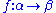is replaced with sequent calculus

Sequent calculus

notation

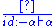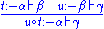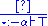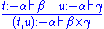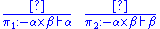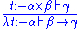Finally, the equations of the category are

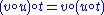
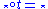
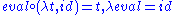
Now, there exists

such that

iff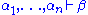

is provable in implicational intuitionistic logic,.

Examples

Thanks to the Curry–Howard correspondence, a typed expression whose type corresponds to a logical formula is analogous to a proof of that formula. Here are examples.

The identity combinator seen as a proof of `α → α` in Hilbert-style logic

As a simple example, we construct a proof of the theorem α → α. In lambda calculus

Lambda calculus

, this is the type of the identity function I = λx.x and in combinatory logic, the identity function is obtained by applying S twice to K. That is, we have I = ((S K) K). As a description of a proof, this says that to prove α → α, we can proceed as follows:

instantiate the second axiom scheme with the formulas α, β → α and α, so that to obtain a proof of (α → ((β → α) → α)) → ((α → (β → α)) → (α → α)),
instantiate the first axiom scheme once with α and β → α, so that to obtain a proof of α → ((β → α) → α),
instantiate the first axiom scheme a second time with α and β, so that to obtain a proof of α → (β → α),
apply modus ponens twice so that to obtain a proof of α → α

In general, the procedure is that whenever the program contains an application of the form (P Q), we should first prove theorems corresponding to the types of P and Q. Since P is being applied to Q, the type of P must have the form α → β and the type of Q must have the form α for some α and β. We can then detach the conclusion, β, via the modus ponens rule.

The composition combinator seen as a proof of `(β → α) → (γ → β) → γ → α` in Hilbert-style logic

As a more complicated example, let's look at the theorem that corresponds to the B function. The type of B is (β → α) → (γ → β) → γ → α. B is equivalent to (S (K S) K). This is our roadmap for the proof of the theorem (β → α) → (γ → β) → γ → α.

First we need to construct (K S). We make the antecedent of the K axiom look like the S axiom by setting α equal to (α → β → γ) → (α → β) → α → γ, and β equal to δ (to avoid variable collisions):

K : α → β → α

K[α = (α → β → γ) → (α → β) → α → γ, β=δ] : ((α → β → γ) → (α → β) → α → γ) → δ → (α → β → γ) → (α → β) → α → γ

Since the antecedent here is just S, we can detach the consequent using Modus Ponens:

K S : δ → (α → β → γ) → (α → β) → α → γ

This is the theorem that corresponds to the type of (K S). We now apply S to this expression. Taking S

S : (α → β → γ) → (α → β) → α → γ

we put α = δ, β = α → β → γ, and γ = (α → β) → α → γ, yielding

S[α = δ, β = α → β → γ, γ = (α → β) → α → γ] : (δ → (α → β → γ) → (α → β) → α → γ) → (δ → (α → β → γ)) → δ → (α → β) → α → γ

and we then detach the consequent:

S (K S) : (δ → α → β → γ) → δ → (α → β) → α → γ

This is the formula for the type of (S (K S)). A special
case of this theorem has δ = (β → γ):

S (K S)[δ = β → γ] : ((β → γ) → α → β → γ) → (β → γ) → (α → β) → α → γ

We need to apply this last formula to K. Again, we specialize K, this time by replacing α with (β → γ) and β with α:

K : α → β → α

K[α = β → γ, β = α] : (β → γ) → α → (β → γ)

This is the same as the antecedent of the prior formula, so we detach the consequent:

S (K S) K : (β → γ) → (α → β) → α → γ

Switching the names of the variables α and γ gives us

(β → α) → (γ → β) → γ → α

which was what we had to prove.

The normal proof of `(β → α) → (γ → β) → γ → α` in natural deduction seen as a λ-term

We give below a proof of (β → α) → (γ → β) → γ → α in natural deduction and show how it can be interpreted as the λ-expression λ a. λb. λ g.(a (b g)) of type (β → α) → (γ → β) → γ → α.

a:β → α, b:γ → β, g:γ b : γ → β a:β → α, b:γ → β, g:γ g : γ
——————————————————————————————————— ————————————————————————————————————————————————————————————————————
a:β → α, b:γ → β, g:γ a : β → α a:β → α, b:γ → β, g:γ b g : β
————————————————————————————————————————————————————————————————————————
a:β → α, b:γ → β, g:γ a (b g) : α
————————————————————————————————————
a:β → α, b:γ → β λ g. a (b g) : γ → α
————————————————————————————————————————
a:β → α λ b. λ g. a (b g) : (γ → β) -> γ → α
————————————————————————————————————
λ a. λ b. λ g. a (b g) : (β → α) -> (γ → β) -> γ → α

Other applications

Recently, the isomorphism has been proposed as a way to define search space partition in Genetic Programming

Genetic programming

In artificial intelligence, genetic programming is an evolutionary algorithm-based methodology inspired by biological evolution to find computer programs that perform a user-defined task. It is a specialization of genetic algorithms where each individual is a computer program...

. The method indexes sets of genotypes (the program trees evolved by the GP system) by their Curry–Howard isomorphic proof (referred to as a species).

Seminal references

, with 2 sections by William Craig, see paragraph 9E.
De Bruijn, Nicolaas (1968), Automath, a language for mathematics, Department of Mathematics, Eindhoven University of Technology, TH-report 68-WSK-05. Reprinted in revised form, with two pages commentary, in: Automation and Reasoning, vol 2, Classical papers on computational logic 1967–1970, Springer Verlag, 1983, pp. 159–200..

Extensions of the correspondence

refs= .... (Full version of the paper presented at Logic Colloquium '90, Helsinki. Abstract in JSL 56(3):1139–1140, 1991.).. (Full version of a paper presented at Logic Colloquium '91, Uppsala. Abstract in JSL 58(2):753–754, 1993.)... (Full version of a paper presented at 2nd WoLLIC'95, Recife. Abstract in Journal of the Interest Group in Pure and Applied Logics 4(2):330–332, 1996.), concerns the adaptation of proofs-as-programs program synthesis to coarse-grain and imperative program development problems, via a method the authors call the Curry–Howard protocol. Includes a discussion of the Curry–Howard correspondence from a Computer Science perspective.. (Full version of a paper presented at LSFA 2010, Natal, Brazil.)

Philosophical interpretations

. (Early version presented at Logic Colloquium '88, Padova. Abstract in JSL 55:425, 1990.). (Early version presented at Fourteenth International Wittgenstein Symposium (Centenary Celebration) held in Kirchberg/Wechsel, August 13–20, 1989.).

Synthetic papers

, the contribution of de Bruijn by himself., contains a synthetic introduction to the Curry–Howard correspondence., contains a synthetic introduction to the Curry–Howard correspondence.

Books

, reproduces the seminal papers of Curry-Feys and Howard, a paper by de Bruijn and a few other papers., notes on proof theory and type theory, that includes a presentation of the Curry–Howard correspondence, with a focus on the formulae-as-types correspondence

Girard, Jean-Yves (1987–90). Proof and Types. Translated by and with appendices by Lafont, Yves and Taylor, Paul. Cambridge University Press (Cambridge Tracts in Theoretical Computer Science, 7), ISBN 0-521-37181-3, notes on proof theory with a presentation of the Curry–Howard correspondence.
Thompson, Simon (1991). Type Theory and Functional Programming Addison–Wesley. ISBN 0-201-41667-0., concerns the adaptation of proofs-as-programs program synthesis to coarse-grain and imperative program development problems, via a method the authors call the Curry–Howard protocol. Includes a discussion of the Curry–Howard correspondence from a Computer Science perspective.
F. Binard and A. Felty, "Genetic programming with polymorphic types and higher-order functions." In Proceedings of the 10th annual conference on Genetic and evolutionary computation, pages 1187 1194, 2008.http://www.site.uottawa.ca/~afelty/dist/gecco08.pdf.

External links

The Curry–Howard Correspondence in Haskell
The Monad Reader 6: Adventures in Classical-Land: Curry–Howard in Haskell, Peirce's law.

The source of this article is wikipedia, the free encyclopedia. The text of this article is licensed under the GFDL.

Origin, scope, and consequences

General formulation

Correspondence between Hilbert-style deduction systems and combinatory logic

Correspondence between natural deduction and lambda calculus

Correspondence between classical logic and control operators

Sequent calculus

The role of de Bruijn

BHK interpretation

Realizability

Curry–Howard–Lambek correspondence

Examples

The identity combinator seen as a proof of α → α in Hilbert-style logic

The composition combinator seen as a proof of (β → α) → (γ → β) → γ → α in Hilbert-style logic

The normal proof of (β → α) → (γ → β) → γ → α in natural deduction seen as a λ-term

Other applications

Seminal references

Extensions of the correspondence

Philosophical interpretations

Synthetic papers

Books

Further reading

External links

The identity combinator seen as a proof of `α → α` in Hilbert-style logic

The composition combinator seen as a proof of `(β → α) → (γ → β) → γ → α` in Hilbert-style logic

The normal proof of `(β → α) → (γ → β) → γ → α` in natural deduction seen as a λ-term