Typed lambda calculus
Encyclopedia
A typed lambda calculus
is a typed formalism
that uses the lambda-symbol (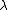
) to denote anonymous function abstraction. In this context, types are usually objects of a syntactic nature that are assigned to lambda terms; the exact nature of a type depends on the calculus considered (see kinds below). From a certain point of view, typed lambda calculi can be seen as refinements of the untyped lambda calculus but from another point of view, they can also be considered the more fundamental theory and untyped lambda calculus a special case with only one type.
Typed lambda calculi are foundational programming languages and are the base of typed functional programming languages such as ML
and Haskell
and, more indirectly, typed imperative programming languages
. Typed lambda calculi play an important role in the design of type systems for programming languages; here typability usually captures desirable properties of the program, e.g. the program will not cause a memory access violation.
Typed lambda calculi are closely related to mathematical logic
and proof theory
via the Curry–Howard isomorphism and they can be considered as the internal language of classes of categories
, e.g. the simply typed lambda calculus is the language of Cartesian closed categories
(CCCs).
are only base types (or type variables) and function types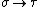
. System T
extends the simply typed lambda calculus with a type of natural numbers and higher order primitive recursion; in this system all functions provably recursive in Peano arithmetic are definable. System F
allows polymorphism by using universal quantification over all types; from a logical perspective it can describe all functions which are provably total in second-order logic
. Lambda calculi with dependent types are the base of intuitionistic type theory
, the calculus of constructions
and the logical framework
(LF), a pure lambda calculus with dependent types. Based on work by Berardi on pure type system
s, Barendregt
proposed the Lambda cube
to systematize the relations of pure typed lambda calculi (including simply typed lambda calculus, System F, LF and the calculus of constructions).
Some typed lambda calculi introduce a notion of subtyping
, i.e. if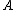
is a subtype of 
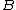, then all terms of type 
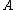also have type 
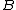. Typed lambda calculi with subtyping are the simply typed lambda calculus with conjunctive types and System F<:.
All the systems mentioned so far, with the exception of the untyped lambda calculus, are strongly normalizing: all computations terminate. As a consequence they are consistent as a logic, i.e. there are uninhabited types. There exist, however, typed lambda calculi that are not strongly normalizing. For example the dependently typed lambda calculus with a type of all types (Type : Type) is not normalizing due to Girard's paradox. This system is also the simplest pure type system, a formalism which generalizes the Lambda cube
. Systems with explicit recursion combinators, such as Plotkin's
PCF, are not normalizing, but they are not intended to be interpreted as a logic. Indeed, PCF
(for Programming language for Computable Functions) is a prototypical, typed functional programming language, where types are used to ensure that programs are well-behaved but not necessarily terminating.
has a notion of "inline agent" that makes it possible to define and manipulate typed lambda expressions directly, through such expressions as agent (p: PERSON): STRING do Result := p.spouse.name end, denoting an object that represents a function which returns a person's spouse's name.
Lambda calculus
In mathematical logic and computer science, lambda calculus, also written as λ-calculus, is a formal system for function definition, function application and recursion. The portion of lambda calculus relevant to computation is now called the untyped lambda calculus...
is a typed formalism
Formalism (mathematics)
In foundations of mathematics, philosophy of mathematics, and philosophy of logic, formalism is a theory that holds that statements of mathematics and logic can be thought of as statements about the consequences of certain string manipulation rules....
that uses the lambda-symbol (
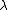) to denote anonymous function abstraction. In this context, types are usually objects of a syntactic nature that are assigned to lambda terms; the exact nature of a type depends on the calculus considered (see kinds below). From a certain point of view, typed lambda calculi can be seen as refinements of the untyped lambda calculus but from another point of view, they can also be considered the more fundamental theory and untyped lambda calculus a special case with only one type.Typed lambda calculi are foundational programming languages and are the base of typed functional programming languages such as ML
ML programming language
ML is a general-purpose functional programming language developed by Robin Milner and others in the early 1970s at the University of Edinburgh, whose syntax is inspired by ISWIM...
and Haskell
Haskell (programming language)
Haskell is a standardized, general-purpose purely functional programming language, with non-strict semantics and strong static typing. It is named after logician Haskell Curry. In Haskell, "a function is a first-class citizen" of the programming language. As a functional programming language, the...
and, more indirectly, typed imperative programming languages
Imperative programming
In computer science, imperative programming is a programming paradigm that describes computation in terms of statements that change a program state...
. Typed lambda calculi play an important role in the design of type systems for programming languages; here typability usually captures desirable properties of the program, e.g. the program will not cause a memory access violation.
Typed lambda calculi are closely related to mathematical logic
Mathematical logic
Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...
and proof theory
Proof theory
Proof theory is a branch of mathematical logic that represents proofs as formal mathematical objects, facilitating their analysis by mathematical techniques. Proofs are typically presented as inductively-defined data structures such as plain lists, boxed lists, or trees, which are constructed...
via the Curry–Howard isomorphism and they can be considered as the internal language of classes of categories
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, e.g. the simply typed lambda calculus is the language of Cartesian closed categories
Cartesian closed category
In category theory, a category is cartesian closed if, roughly speaking, any morphism defined on a product of two objects can be naturally identified with a morphism defined on one of the factors. These categories are particularly important in mathematical logic and the theory of programming, in...
(CCCs).
Kinds of typed lambda calculi
Various typed lambda calculi have been studied: The types of the simply typed lambda calculusSimply typed lambda calculus
The simply typed lambda calculus , a formof type theory, is a typed interpretation of the lambda calculus with only one type constructor: \to that builds function types. It is the canonical and simplest example of a typed lambda calculus...
are only base types (or type variables) and function types
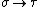. System TSystem T
In mathematics, System T can refer to:* A theory of arithmetic in all finite types use in Gödel's Dialectica interpretation* An axiom system of modal logic...
extends the simply typed lambda calculus with a type of natural numbers and higher order primitive recursion; in this system all functions provably recursive in Peano arithmetic are definable. System F
System F
System F, also known as the polymorphic lambda calculus or the second-order lambda calculus, is a typed lambda calculus that differs from the simply typed lambda calculus by the introduction of a mechanism of universal quantification over types...
allows polymorphism by using universal quantification over all types; from a logical perspective it can describe all functions which are provably total in second-order logic
Second-order logic
In logic and mathematics second-order logic is an extension of first-order logic, which itself is an extension of propositional logic. Second-order logic is in turn extended by higher-order logic and type theory....
. Lambda calculi with dependent types are the base of intuitionistic type theory
Intuitionistic type theory
Intuitionistic type theory, or constructive type theory, or Martin-Löf type theory or just Type Theory is a logical system and a set theory based on the principles of mathematical constructivism. Intuitionistic type theory was introduced by Per Martin-Löf, a Swedish mathematician and philosopher,...
, the calculus of constructions
Calculus of constructions
The calculus of constructions is a formal language in which both computer programs and mathematical proofs can be expressed. This language forms the basis of theory behind the Coq proof assistant, which implements the derivative calculus of inductive constructions.-General traits:The CoC is a...
and the logical framework
LF (logical framework)
In logic, a logical framework provides a means to define a logic as a signature in a higher-order type theory in such a way that provability of a formula in the original logic reduces to a type inhabitation problem in the framework type theory. This approach has been used successfully for ...
(LF), a pure lambda calculus with dependent types. Based on work by Berardi on pure type system
Pure type system
In the branches of mathematical logic known as proof theory and type theory, a pure type system , previously known as a generalized type system , is a form of typed lambda calculus that allows an arbitrary number of sorts and dependencies between any of these...
s, Barendregt
Barendregt
* Jaap Barendregt , a Dutch footballer* Hendrik Pieter Barendregt , a Dutch logician* Barendregt convention* Barendregt-Geuvers-Klop conjecture...
proposed the Lambda cube
Lambda cube
In mathematical logic and type theory, the λ-cube is a framework for exploring the axes of refinement in Coquand's calculus of constructions, starting from the simply typed lambda calculus as the vertex of a cube placed at the origin, and the calculus of constructions as its diametrically opposite...
to systematize the relations of pure typed lambda calculi (including simply typed lambda calculus, System F, LF and the calculus of constructions).
Some typed lambda calculi introduce a notion of subtyping
Subtype
In programming language theory, subtyping or subtype polymorphism is a form of type polymorphism in which a subtype is a datatype that is related to another datatype by some notion of substitutability, meaning that program constructs, typically subroutines or functions, written to operate on...
, i.e. if
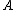is a subtype of 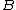, then all terms of type 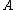also have type 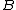. Typed lambda calculi with subtyping are the simply typed lambda calculus with conjunctive types and System F<:.All the systems mentioned so far, with the exception of the untyped lambda calculus, are strongly normalizing: all computations terminate. As a consequence they are consistent as a logic, i.e. there are uninhabited types. There exist, however, typed lambda calculi that are not strongly normalizing. For example the dependently typed lambda calculus with a type of all types (Type : Type) is not normalizing due to Girard's paradox. This system is also the simplest pure type system, a formalism which generalizes the Lambda cube
Lambda cube
In mathematical logic and type theory, the λ-cube is a framework for exploring the axes of refinement in Coquand's calculus of constructions, starting from the simply typed lambda calculus as the vertex of a cube placed at the origin, and the calculus of constructions as its diametrically opposite...
. Systems with explicit recursion combinators, such as Plotkin's
Gordon Plotkin
Gordon D. Plotkin, FRS, FRSE is a Scottish computer scientist.Gordon Plotkin is best-known for his introduction of structural operational semantics and his work on denotational semantics. In particular, his notes on A Structural Approach to Operational Semantics of 1981 were very influential...
PCF, are not normalizing, but they are not intended to be interpreted as a logic. Indeed, PCF
Programming language for Computable Functions
In computer science, Programming Computable Functions,"PCF is a programming language for computable functions, based on LCF, Scott’s logic of computable functions" . Programming Computable Functions is used by . It is also referred to as Programming with Computable Functions or Programming language...
(for Programming language for Computable Functions) is a prototypical, typed functional programming language, where types are used to ensure that programs are well-behaved but not necessarily terminating.
Applications to programming languages
In programming, the routines (functions, procedures, methods) of strongly typed programming languages closely correspond to typed lambda expressions. EiffelEiffel (programming language)
Eiffel is an ISO-standardized, object-oriented programming language designed by Bertrand Meyer and Eiffel Software. The design of the language is closely connected with the Eiffel programming method...
has a notion of "inline agent" that makes it possible to define and manipulate typed lambda expressions directly, through such expressions as agent (p: PERSON): STRING do Result := p.spouse.name end, denoting an object that represents a function which returns a person's spouse's name.
See Also
- Kappa calculusKappa calculusIn mathematical logic, category theory, andcomputer science, kappa calculus is aformal system for defining first-orderfunctions.Unlike lambda calculus, kappa calculus has nohigher-order functions; its functions arenot first class objects...
-- an analogue of typed lambda calculus which excludes higher-order functions