Hilbert-style deduction system
Encyclopedia
In logic
, especially mathematical logic
, a Hilbert system, sometimes called Hilbert calculus or Hilbert–Ackermann system, is a type of system of formal deduction
attributed to Gottlob Frege
and David Hilbert
. These deductive system
s are most often studied for first-order logic
, but are of interest for other logics as well.
Most variants of Hilbert systems take a characteristic tack in the way they balance a trade-off
between logical axioms and rules of inference
. Hilbert systems can be characterised by the choice of a large number of schemes
of logical axioms and a small set of rules of inference
. The most commonly studied Hilbert systems have either just one rule of inference —modus ponens
, for propositional logics— or two — with generalisation
, to handle predicate logic
s, as well— and several infinite axiom schemes. Hilbert systems for propositional modal logic
s, sometimes called Hilbert-Lewis systems, are generally axiomatised with two additional rules, the necessitation rule and the uniform substitution rule.
A characteristic feature of the many variants of Hilbert systems is that the context is not changed in any of their rules of inference, while both natural deduction
and sequent calculus
contain some context-changing rules. Thus, if we are interested only in the derivability of tautologies
, no hypothetical judgments, then we can formalize the Hilbert system in such a way that its rules of inference contain only judgment
s of a rather simple form. The same cannot be done with the other two deductions systems: as context is changed in some of their rules of inferences, they cannot be formalized so that hypothetical judgments could be avoided — not even if we want to use them just for proving derivability of tautologies.
Systems of natural deduction
take the opposite tack, including many deduction rules but very few or no axiom schemes.
Suppose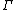
is a set of formulas, considered as hypotheses. For example 
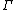could be a set of axioms for group theory
or set theory
. The notation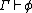
means that there is a deduction that ends with 
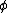using as axioms only logical axioms and elements of 
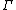. Thus, informally, 
means that 
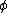is provable assuming all the formulas in 
.
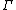Hilbert-style deduction systems are characterized by the use of numerous schemes of logical axioms. An axiom scheme is an infinite set of axioms obtained by substituting all formulas of some form into a specific pattern. The set of logical axioms includes not only those axioms generated from this pattern, but also any generalization of one of those axioms. A generalization of a formula is obtained by prefixing zero or more universal quantifiers on the formula; thus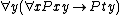
is a generalization of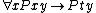
.
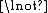and 
and only the quantifier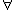 
. Later we show how the system can be extended to include additional logical connectives, such as 
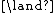and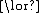 
, without enlarging the class of deducible formulas.
The first four logical axiom schemes allow (together with modus ponens) for the manipulation of logical connectives.
The axiom P1 is redundant, as it follows from P3, P2 and modus ponens. These axioms describe classical propositional logic; without axiom P4 we get (minimal) intuitionistic logic
. Full intuitionistic logic is achieved by adding instead the axiom P4i for ex falso quodlibet, which is an axiom of classical propositional logic.
Note that these are axiom schemes, which represent infinitely many specific instances of axioms. For example, P1 might represent the particular axiom instance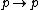
, or it might represent 
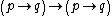: the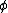 
is a place where any formula can be placed. A variable such as this that ranges over formulae is called a 'schematic variable'.
With a second rule of uniform substitution (US), we can change each of these axiom schemes into a single axiom, replacing each schematic variable by some propositional variable that isn't mentioned in any axiom to get what we call the substitutional axiomatisation. Both formalisations have variables, but where the one-rule axiomatisation has schematic variables that are outside the logic's language, the substitutional axiomatisation uses propositional variables that do the same work by expressing the idea of a variable ranging over formulae with a rule that uses substitution.
The next three logical axiom schemes provide ways to add, manipulate, and remove universal quantifiers.
These three additional rules extend the propositional system to axiomatise classical predicate logic. Likewise, these three rules extend system for intuitionstic propositional logic (with P1-3 and P4i) to intuitionistic predicate logic.
Universal quantification is often given an alternative axiomatisation using an extra rule of generalisation (see the section on Metatheorems), in which case the rules Q5 and Q6 are redundant.
The final axiom schemes are required to work with formulas involving the equality symbol.
s of the deduction theorem
that permit the use of additional connectives. These extensions are called conservative because if a formula φ involving new connectives is rewritten as a logically equivalent
formula θ involving only negation, implication, and universal quantification, then φ is derivable in the extended system if and only if θ is derivable in the original system. When fully extended, a Hilbert-style system will resemble more closely a system of natural deduction
.
Some common metatheorems of this form are:
had axioms P2 and P3 but four other axioms instead of axiom P4 (see Frege's propositional calculus
).
Russell
and Whitehead
also suggested a system with five propositional axioms.
base combinators I, K and S with the application operator. Proofs in the Hilbert system then correspond to combinator terms in combinatory logic. See also Curry-Howard correspondence.
).
Logic
In philosophy, Logic is the formal systematic study of the principles of valid inference and correct reasoning. Logic is used in most intellectual activities, but is studied primarily in the disciplines of philosophy, mathematics, semantics, and computer science...
, especially mathematical logic
Mathematical logic
Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...
, a Hilbert system, sometimes called Hilbert calculus or Hilbert–Ackermann system, is a type of system of formal deduction
Deductive reasoning
Deductive reasoning, also called deductive logic, is reasoning which constructs or evaluates deductive arguments. Deductive arguments are attempts to show that a conclusion necessarily follows from a set of premises or hypothesis...
attributed to Gottlob Frege
Gottlob Frege
Friedrich Ludwig Gottlob Frege was a German mathematician, logician and philosopher. He is considered to be one of the founders of modern logic, and made major contributions to the foundations of mathematics. He is generally considered to be the father of analytic philosophy, for his writings on...
and David Hilbert
David Hilbert
David Hilbert was a German mathematician. He is recognized as one of the most influential and universal mathematicians of the 19th and early 20th centuries. Hilbert discovered and developed a broad range of fundamental ideas in many areas, including invariant theory and the axiomatization of...
. These deductive system
Deductive system
A deductive system consists of the axioms and rules of inference that can be used to derive the theorems of the system....
s are most often studied for first-order logic
First-order logic
First-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
, but are of interest for other logics as well.
Most variants of Hilbert systems take a characteristic tack in the way they balance a trade-off
Trade-off
A trade-off is a situation that involves losing one quality or aspect of something in return for gaining another quality or aspect...
between logical axioms and rules of inference
Rule of inference
In logic, a rule of inference, inference rule, or transformation rule is the act of drawing a conclusion based on the form of premises interpreted as a function which takes premises, analyses their syntax, and returns a conclusion...
. Hilbert systems can be characterised by the choice of a large number of schemes
Axiom schema
In mathematical logic, an axiom schema generalizes the notion of axiom.An axiom schema is a formula in the language of an axiomatic system, in which one or more schematic variables appear. These variables, which are metalinguistic constructs, stand for any term or subformula of the system, which...
of logical axioms and a small set of rules of inference
Rule of inference
In logic, a rule of inference, inference rule, or transformation rule is the act of drawing a conclusion based on the form of premises interpreted as a function which takes premises, analyses their syntax, and returns a conclusion...
. The most commonly studied Hilbert systems have either just one rule of inference —modus ponens
Modus ponens
In classical logic, modus ponendo ponens or implication elimination is a valid, simple argument form. It is related to another valid form of argument, modus tollens. Both Modus Ponens and Modus Tollens can be mistakenly used when proving arguments...
, for propositional logics— or two — with generalisation
Generalization (logic)
In mathematical logic, generalization is an inference rule of predicate calculus. It states that if \vdash P has been derived, then \vdash \forall x \, P can be derived....
, to handle predicate logic
Predicate logic
In mathematical logic, predicate logic is the generic term for symbolic formal systems like first-order logic, second-order logic, many-sorted logic or infinitary logic. This formal system is distinguished from other systems in that its formulae contain variables which can be quantified...
s, as well— and several infinite axiom schemes. Hilbert systems for propositional modal logic
Modal logic
Modal logic is a type of formal logic that extends classical propositional and predicate logic to include operators expressing modality. Modals — words that express modalities — qualify a statement. For example, the statement "John is happy" might be qualified by saying that John is...
s, sometimes called Hilbert-Lewis systems, are generally axiomatised with two additional rules, the necessitation rule and the uniform substitution rule.
A characteristic feature of the many variants of Hilbert systems is that the context is not changed in any of their rules of inference, while both natural deduction
Natural deduction
In logic and proof theory, natural deduction is a kind of proof calculus in which logical reasoning is expressed by inference rules closely related to the "natural" way of reasoning...
and sequent calculus
Sequent calculus
In proof theory and mathematical logic, sequent calculus is a family of formal systems sharing a certain style of inference and certain formal properties. The first sequent calculi, systems LK and LJ, were introduced by Gerhard Gentzen in 1934 as a tool for studying natural deduction in...
contain some context-changing rules. Thus, if we are interested only in the derivability of tautologies
Tautology (logic)
In logic, a tautology is a formula which is true in every possible interpretation. Philosopher Ludwig Wittgenstein first applied the term to redundancies of propositional logic in 1921; it had been used earlier to refer to rhetorical tautologies, and continues to be used in that alternate sense...
, no hypothetical judgments, then we can formalize the Hilbert system in such a way that its rules of inference contain only judgment
Judgment (mathematical logic)
In mathematical logic, a judgment can be for example an assertion about occurrence of a free variable in an expression of the object language, or about provability of a proposition ; but judgments can be also other inductively definable assertions in the metatheory...
s of a rather simple form. The same cannot be done with the other two deductions systems: as context is changed in some of their rules of inferences, they cannot be formalized so that hypothetical judgments could be avoided — not even if we want to use them just for proving derivability of tautologies.
Systems of natural deduction
Natural deduction
In logic and proof theory, natural deduction is a kind of proof calculus in which logical reasoning is expressed by inference rules closely related to the "natural" way of reasoning...
take the opposite tack, including many deduction rules but very few or no axiom schemes.
Formal deductions
In a Hilbert-style deduction system, a formal deduction is a finite sequence of formulas in which each formula is either an axiom or is obtained from previous formulas by a rule of inference. These formal deductions are meant to mirror natural-language proofs, although they are far more detailed.Suppose
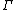is a set of formulas, considered as hypotheses. For example 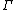could be a set of axioms for group theoryGroup theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
or set theory
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
. The notation
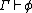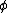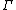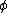means that there is a deduction that ends with using as axioms only logical axioms and elements of . Thus, informally, means that is provable assuming all the formulas in 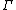.Hilbert-style deduction systems are characterized by the use of numerous schemes of logical axioms. An axiom scheme is an infinite set of axioms obtained by substituting all formulas of some form into a specific pattern. The set of logical axioms includes not only those axioms generated from this pattern, but also any generalization of one of those axioms. A generalization of a formula is obtained by prefixing zero or more universal quantifiers on the formula; thus
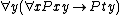
is a generalization of
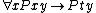.Logical axioms
There are several variant axiomatisations of predicate logic, since for any logic there is freedom in choosing axioms and rules that characterise that logic. We describe here a Hilbert system with nine axioms and just the rule modus ponens, which we call the one-rule axiomatisation and which describes classical equational logic. We deal with a minimal language for this logic, where formulas use only the connectives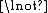 and and only the quantifier 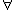. Later we show how the system can be extended to include additional logical connectives, such as 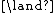and 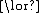, without enlarging the class of deducible formulas.The first four logical axiom schemes allow (together with modus ponens) for the manipulation of logical connectives.
- P1.
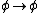
- P2.
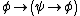
- P3.
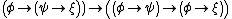
- P4.
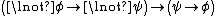
The axiom P1 is redundant, as it follows from P3, P2 and modus ponens. These axioms describe classical propositional logic; without axiom P4 we get (minimal) intuitionistic logic
Intuitionistic logic
Intuitionistic logic, or constructive logic, is a symbolic logic system differing from classical logic in its definition of the meaning of a statement being true. In classical logic, all well-formed statements are assumed to be either true or false, even if we do not have a proof of either...
. Full intuitionistic logic is achieved by adding instead the axiom P4i for ex falso quodlibet, which is an axiom of classical propositional logic.
- P4i.
Note that these are axiom schemes, which represent infinitely many specific instances of axioms. For example, P1 might represent the particular axiom instance
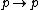, or it might represent 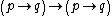: the 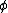is a place where any formula can be placed. A variable such as this that ranges over formulae is called a 'schematic variable'.With a second rule of uniform substitution (US), we can change each of these axiom schemes into a single axiom, replacing each schematic variable by some propositional variable that isn't mentioned in any axiom to get what we call the substitutional axiomatisation. Both formalisations have variables, but where the one-rule axiomatisation has schematic variables that are outside the logic's language, the substitutional axiomatisation uses propositional variables that do the same work by expressing the idea of a variable ranging over formulae with a rule that uses substitution.
- US. Let
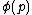be a formula with one or more instances of the propositional variable 
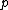, and let 
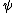be another formula. Then from 
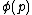, infer 
.
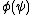The next three logical axiom schemes provide ways to add, manipulate, and remove universal quantifiers.
- Q5.
where t may be substituted for x in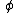 
- Q6.
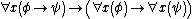
- Q7.
where x is not a free variable of 
.
These three additional rules extend the propositional system to axiomatise classical predicate logic. Likewise, these three rules extend system for intuitionstic propositional logic (with P1-3 and P4i) to intuitionistic predicate logic.
Universal quantification is often given an alternative axiomatisation using an extra rule of generalisation (see the section on Metatheorems), in which case the rules Q5 and Q6 are redundant.
The final axiom schemes are required to work with formulas involving the equality symbol.
- I8.
for every variable x. - I9.
Conservative extensions
It is common to include in a Hilbert-style deduction system only axioms for implication and negation. Given these axioms, it is possible to form conservative extensionConservative extension
In mathematical logic, a logical theory T_2 is a conservative extension of a theory T_1 if the language of T_2 extends the language of T_1; every theorem of T_1 is a theorem of T_2; and any theorem of T_2 which is in the language of T_1 is already a theorem of T_1.More generally, if Γ is a set of...
s of the deduction theorem
Deduction theorem
In mathematical logic, the deduction theorem is a metatheorem of first-order logic. It is a formalization of the common proof technique in which an implication A → B is proved by assuming A and then proving B from this assumption. The deduction theorem explains why proofs of conditional...
that permit the use of additional connectives. These extensions are called conservative because if a formula φ involving new connectives is rewritten as a logically equivalent
Logical equivalence
In logic, statements p and q are logically equivalent if they have the same logical content.Syntactically, p and q are equivalent if each can be proved from the other...
formula θ involving only negation, implication, and universal quantification, then φ is derivable in the extended system if and only if θ is derivable in the original system. When fully extended, a Hilbert-style system will resemble more closely a system of natural deduction
Natural deduction
In logic and proof theory, natural deduction is a kind of proof calculus in which logical reasoning is expressed by inference rules closely related to the "natural" way of reasoning...
.
Existential quantification
- Introduction
- Elimination
where 
is not a free variable of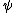 
.
Conjunction and Disjunction
- Conjunction introduction and elimination
- introduction:
- elimination left:
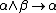
- elimination right:
- Disjunction introduction and elimination
- introduction left:
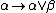
- introduction right:
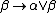
- elimination:
Metatheorems
Because Hilbert-style systems have very few deduction rules, it is common to prove metatheorems that show that additional deduction rules add no deductive power, in the sense that a deduction using the new deduction rules can be converted into a deduction using only the original deduction rules.Some common metatheorems of this form are:
- The deduction theorem:
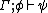if and only if 
. -
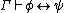if and only if 
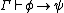and 
. - Contraposition: If
then 
. - Generalization: If
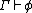and x does not occur free in any formula of 
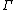then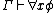 
.
Alternative axiomatizations
The axiom 3 above is credited to Łukasiewicz. The original system by FregeGottlob Frege
Friedrich Ludwig Gottlob Frege was a German mathematician, logician and philosopher. He is considered to be one of the founders of modern logic, and made major contributions to the foundations of mathematics. He is generally considered to be the father of analytic philosophy, for his writings on...
had axioms P2 and P3 but four other axioms instead of axiom P4 (see Frege's propositional calculus
Frege's propositional calculus
In mathematical logic Frege's propositional calculus was the first axiomatization of propositional calculus. It was invented by Gottlob Frege, who also invented predicate calculus, in 1879 as part of his second-order predicate calculus .It...
).
Russell
Bertrand Russell
Bertrand Arthur William Russell, 3rd Earl Russell, OM, FRS was a British philosopher, logician, mathematician, historian, and social critic. At various points in his life he considered himself a liberal, a socialist, and a pacifist, but he also admitted that he had never been any of these things...
and Whitehead
Alfred North Whitehead
Alfred North Whitehead, OM FRS was an English mathematician who became a philosopher. He wrote on algebra, logic, foundations of mathematics, philosophy of science, physics, metaphysics, and education...
also suggested a system with five propositional axioms.
Further connections
Axioms P1, P2 and P3, with the deduction rule modus ponens (formalising intuitionistic propositional logic), correspond to combinatory logicCombinatory logic
Combinatory logic is a notation introduced by Moses Schönfinkel and Haskell Curry to eliminate the need for variables in mathematical logic. It has more recently been used in computer science as a theoretical model of computation and also as a basis for the design of functional programming...
base combinators I, K and S with the application operator. Proofs in the Hilbert system then correspond to combinator terms in combinatory logic. See also Curry-Howard correspondence.
External links
It describes (among others) a part of the Hilbert-style deduction system (restricted to propositional calculusPropositional calculus
In mathematical logic, a propositional calculus or logic is a formal system in which formulas of a formal language may be interpreted as representing propositions. A system of inference rules and axioms allows certain formulas to be derived, called theorems; which may be interpreted as true...
).