Type inhabitation problem
Encyclopedia
In type theory
, a branch of mathematical logic
, in a given typed calculus, the type inhabitation problem for this calculus is the following problem: given a type
and a type environment 
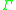, does there exist a 
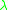-term M such that 
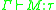? With an empty type environment, such an M is said to be an inhabitant of 
.
, a type has an inhabitant if and only if its corresponding proposition is a tautology
of minimal implicative logic. Similarly, a System F
type has an inhabitant if and only if its corresponding proposition is a tautology of second-order logic
.
proved that for simply typed lambda calculus
the type inhabitation problem is PSPACE-complete
. For other calculi, like System F
, the problem is even undecidable
.
Type theory
In mathematics, logic and computer science, type theory is any of several formal systems that can serve as alternatives to naive set theory, or the study of such formalisms in general...
, a branch of mathematical logic
Mathematical logic
Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...
, in a given typed calculus, the type inhabitation problem for this calculus is the following problem: given a type
and a type environment 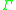, does there exist a 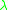-term M such that 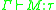? With an empty type environment, such an M is said to be an inhabitant of .Relationship to logic
In the case of simply typed lambda calculusSimply typed lambda calculus
The simply typed lambda calculus , a formof type theory, is a typed interpretation of the lambda calculus with only one type constructor: \to that builds function types. It is the canonical and simplest example of a typed lambda calculus...
, a type has an inhabitant if and only if its corresponding proposition is a tautology
Tautology (logic)
In logic, a tautology is a formula which is true in every possible interpretation. Philosopher Ludwig Wittgenstein first applied the term to redundancies of propositional logic in 1921; it had been used earlier to refer to rhetorical tautologies, and continues to be used in that alternate sense...
of minimal implicative logic. Similarly, a System F
System F
System F, also known as the polymorphic lambda calculus or the second-order lambda calculus, is a typed lambda calculus that differs from the simply typed lambda calculus by the introduction of a mechanism of universal quantification over types...
type has an inhabitant if and only if its corresponding proposition is a tautology of second-order logic
Second-order logic
In logic and mathematics second-order logic is an extension of first-order logic, which itself is an extension of propositional logic. Second-order logic is in turn extended by higher-order logic and type theory....
.
Formal properties
For most typed calculus, the type inhabitation problem is very hard. Richard StatmanRichard Statman
Richard Statman is an American computer scientist whose principal research interest is the theory of computation, especially symbolic computation. His research involves lambda calculus, type theory and combinatory algebra.-Career:...
proved that for simply typed lambda calculus
Simply typed lambda calculus
The simply typed lambda calculus , a formof type theory, is a typed interpretation of the lambda calculus with only one type constructor: \to that builds function types. It is the canonical and simplest example of a typed lambda calculus...
the type inhabitation problem is PSPACE-complete
PSPACE-complete
In complexity theory, a decision problem is PSPACE-complete if it is in the complexity class PSPACE, and every problem in PSPACE can be reduced to it in polynomial time...
. For other calculi, like System F
System F
System F, also known as the polymorphic lambda calculus or the second-order lambda calculus, is a typed lambda calculus that differs from the simply typed lambda calculus by the introduction of a mechanism of universal quantification over types...
, the problem is even undecidable
Decision problem
In computability theory and computational complexity theory, a decision problem is a question in some formal system with a yes-or-no answer, depending on the values of some input parameters. For example, the problem "given two numbers x and y, does x evenly divide y?" is a decision problem...
.