In mathematical logic

Mathematical logic

Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...

 and computer science

Computer science

Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...

, the lambda-mu calculus is an extension of the lambda calculus

Lambda calculus

In mathematical logic and computer science, lambda calculus, also written as λ-calculus, is a formal system for function definition, function application and recursion. The portion of lambda calculus relevant to computation is now called the untyped lambda calculus...

, and was introduced by M. Parigot. It introduces two new operators: the mu

Mu

- Language :* Mu , Μ or μ, a letter in the Greek alphabet* Mu , represented by the Japanese kana む or ム* 無, Mu , a Japanese and Korean word important in Zen practice...

 operator (which is completely different both from the mu operator

Mu operator

In computability theory, the μ operator, minimization operator, or unbounded search operator searches for the least natural number with a given property.- Definition :...

 found in computability theory

Computability theory

Computability theory, also called recursion theory, is a branch of mathematical logic that originated in the 1930s with the study of computable functions and Turing degrees. The field has grown to include the study of generalized computability and definability...

 and from the μ operator of modal μ-calculus) and the bracket operator. Proof-theoretically

Proof theory

Proof theory is a branch of mathematical logic that represents proofs as formal mathematical objects, facilitating their analysis by mathematical techniques. Proofs are typically presented as inductively-defined data structures such as plain lists, boxed lists, or trees, which are constructed...

, it provides a well-behaved formulation of Classical natural deduction.

One of the main goals of this extended calculus is to be able to describe expressions corresponding to theorems in classical logic

Classical logic

Classical logic identifies a class of formal logics that have been most intensively studied and most widely used. The class is sometimes called standard logic as well...

. According to the Curry–Howard isomorphism, lambda calculus on its own can express theorems in intuitionistic logic

Intuitionistic logic

Intuitionistic logic, or constructive logic, is a symbolic logic system differing from classical logic in its definition of the meaning of a statement being true. In classical logic, all well-formed statements are assumed to be either true or false, even if we do not have a proof of either...

 only, and several classical logical theorems can't be written at all. However with these new operators one is able to write terms that have the type of, for example the law of noncontradiction

Law of noncontradiction

In classical logic, the law of non-contradiction is the second of the so-called three classic laws of thought. It states that contradictory statements cannot both at the same time be true, e.g...

, or Peirce's law

Peirce's law

In logic, Peirce's law is named after the philosopher and logician Charles Sanders Peirce. It was taken as an axiom in his first axiomatisation of propositional logic. It can be thought of as the law of excluded middle written in a form that involves only one sort of connective, namely...

.

Semantically these operators correspond to continuations found in some functional programming languages.

Formal definition

We can augment the definition of a lambda expression to gain one in the context of lambda-mu calculus. The three main expressions found in lambda calculus are as follows:

1. V, a variable, where V is any identifier
   Identifier
   An identifier is a name that identifies either a unique object or a unique class of objects, where the "object" or class may be an idea, physical [countable] object , or physical [noncountable] substance...
   
   .
2. λV.E, an abstraction, where V is any identifier and E is any lambda expression.
3. (E E′), an application, where E and E′ are any lambda expressions.

For details, see the corresponding article.

In addition to the traditional λ-variables, the lambda-mu calculus includes a distinct set of μ-variables. These μ-variables can be used to name or freeze arbitrary subterms, allowing us to later abstract on those names. The set of terms contains unnamed (all traditional lambda expressions are of this kind) and named terms. The terms that are added by the lambda-mu calculus are of the form:

1. [α]t is a named term, where α is a μ-variable and t is an unnamed term.
2. (μ α. E) is an unnamed term, where α is a μ-variable and E is a named term.

Reduction

The basic reduction rules used in the lambda-mu calculus are the following:

logical reduction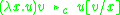
structural reduction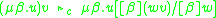
renaming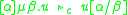
the equivalent of η-reduction	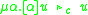, for α not freely occurring in u

These rules cause the calculus to be confluent

Confluence (term rewriting)

In computer science, confluence is a property of rewriting systems, describing that terms in this system can be rewritten in more than one way, to yield the same result. This article describes the properties in the most abstract setting of an abstract rewriting system.- Motivating example :Consider...

. Further reduction rules could be added to provide us with a stronger notion of normal form, though this would be at the expense of confluence.

See also

• Lambda Calculus
  Lambda calculus
  In mathematical logic and computer science, lambda calculus, also written as λ-calculus, is a formal system for function definition, function application and recursion. The portion of lambda calculus relevant to computation is now called the untyped lambda calculus...
  
  
• Classical pure type systems for typed generalizations of lambda calculi with control

External links

• Lambda-mu relevant discussion on Lambda the Ultimate.