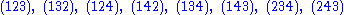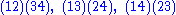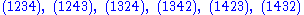Cycle notation
Encyclopedia
In combinatorial
mathematics
, the cycle notation is a useful convention for writing down a permutation
in terms of its constituent cycle
s. This is also called circular notation and the permutation called a cyclic or circular permutation.
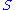 be a finite set, and
be a finite set, and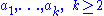
be distinct elements of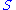 . The expression
. The expression
denotes the cycle σ whose action
is
For each index i,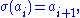
where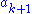 is taken to mean
is taken to mean 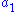 .
.
There are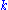 different expressions for the same cycle; the following all represent the same cycle:
different expressions for the same cycle; the following all represent the same cycle:
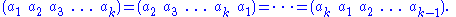
A 1-element cycle such as (3) is the identity
permutation. The identity permutation can also be written as an empty cycle, "".
 be a permutation of
be a permutation of 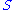 , and let
, and let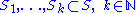
be the orbits of with more than 1 element. Consider an element
with more than 1 element. Consider an element 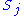 ,
,  , let
, let 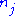 denote the cardinality of
denote the cardinality of 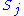 ,
,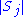 =
=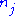 . Also, choose an
. Also, choose an 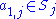 , and define
, and define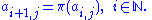
We can now express as a product of disjoint cycles, namely
as a product of disjoint cycles, namely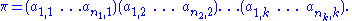
Note that the usual convention in cycle notation is to multiply from left to right (in contrast with composition of functions
, which is normally done from right to left). For example, the product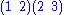 is equal to
is equal to 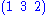 not
not 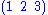 .
.
on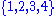 expressed using the cycle notation, and grouped according to their conjugacy class
expressed using the cycle notation, and grouped according to their conjugacy class
es:
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the cycle notation is a useful convention for writing down a permutation
Permutation
In mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
in terms of its constituent cycle
Cycle (mathematics)
In mathematics, and in particular in group theory, a cycle is a permutation of the elements of some set X which maps the elements of some subset S to each other in a cyclic fashion, while fixing all other elements...
s. This is also called circular notation and the permutation called a cyclic or circular permutation.
Definition
Let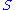 be a finite set, and
be a finite set, and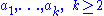
be distinct elements of
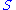 . The expression
. The expression
denotes the cycle σ whose action
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
is

For each index i,
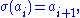
where
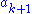 is taken to mean
is taken to mean 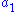 .
.There are
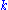 different expressions for the same cycle; the following all represent the same cycle:
different expressions for the same cycle; the following all represent the same cycle: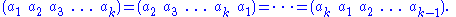
A 1-element cycle such as (3) is the identity
Identity function
In mathematics, an identity function, also called identity map or identity transformation, is a function that always returns the same value that was used as its argument...
permutation. The identity permutation can also be written as an empty cycle, "".
Permutation as product of cycles
Let be a permutation of
be a permutation of 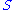 , and let
, and let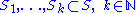
be the orbits of
 with more than 1 element. Consider an element
with more than 1 element. Consider an element 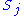 ,
,  , let
, let 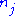 denote the cardinality of
denote the cardinality of 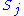 ,
,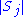 =
=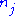 . Also, choose an
. Also, choose an 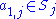 , and define
, and define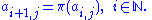
We can now express
 as a product of disjoint cycles, namely
as a product of disjoint cycles, namely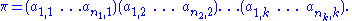
Note that the usual convention in cycle notation is to multiply from left to right (in contrast with composition of functions
Function composition
In mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
, which is normally done from right to left). For example, the product
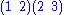 is equal to
is equal to 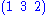 not
not 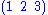 .
.Example
Here are the 24 elements of the symmetric groupSymmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
on
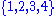 expressed using the cycle notation, and grouped according to their conjugacy class
expressed using the cycle notation, and grouped according to their conjugacy classConjugacy class
In mathematics, especially group theory, the elements of any group may be partitioned into conjugacy classes; members of the same conjugacy class share many properties, and study of conjugacy classes of non-abelian groups reveals many important features of their structure...
es:


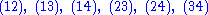 (
(