Vertex separator
Encyclopedia
In graph theory
, a vertex subset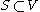
is a vertex separator for nonadjacent vertices 
and 
if the removal of 
from the graph separates 
and 
into distinct connected component
s.
To give another class of examples, every free tree T has a separator S consisting of a single vertex, the removal of which
partitions T into two or more connected components, each of size at most n/2. More precisely, there is always exactly one or exactly
two vertices, which amount to such a separator, depending on whether the tree is centered
or bicentered
.
As opposed to these examples, not all vertex separators are balanced, but that property is most useful for applications in computer science, such as the planar separator theorem
.
Lemma. A vertex separator S in G is minimal if and only if the graph
, obtained by removing S from G, has two connected components 
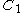and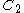 
such that each vertex in S is both adjacent to some vertex in 
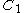and to some vertex in 
.
The minimal separators also form an algebraic structure
: For two fixed vertices a and b of a given graph G, an (a,b)-separator S can be regarded as a predecessor of another (a,b)-separator T, if every path from a to b meets S before it meets T. More rigorously, the predecessor relation is defined as follows: Let S and T be two (a,b)-separators in 'G'. Then S is a predecessor of T, in symbols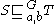
, if for each 
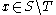, every path connecting x to b meets T. It follows from the definition that the predecessor relation yields a preorder
on the set of all (a,b)-separators. Furthermore, proved that the predecessor relation gives rise to a complete lattice
when restricted to the set of minimal (a,b)-separators in G.
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, a vertex subset
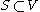is a vertex separator for nonadjacent vertices and if the removal of from the graph separates and into distinct connected componentConnected component (graph theory)
In graph theory, a connected component of an undirected graph is a subgraph in which any two vertices are connected to each other by paths, and which is connected to no additional vertices. For example, the graph shown in the illustration on the right has three connected components...
s.
Examples
Consider a grid graph with r rows and c columns; the total number n of vertices is r*c. For instance, in the illustration, r = 5, c = 8, and n = 40. If r is odd, there is a single central row, and otherwise there are two rows equally close to the center; similarly, if c is odd, there is a single central column, and otherwise there are two columns equally close to the center. Choosing S to be any of these central rows or columns, and removing S from the graph, partitions the graph into two smaller connected subgraphs A and B, each of which has at most n/2 vertices. If r ≤ c (as in the illustration), then choosing a central column will give a separator S with r ≤ √n vertices, and similarly if c ≤ r then choosing a central row will give a separator with at most √n vertices. Thus, every grid graph has a separator S of size at most √n, the removal of which partitions it into two connected components, each of size at most n/2.partitions T into two or more connected components, each of size at most n/2. More precisely, there is always exactly one or exactly
two vertices, which amount to such a separator, depending on whether the tree is centered
Centered tree
In discrete mathematics, a centered tree is a tree with only one center, and a bicentered tree is a tree with two centers.Given a graph, the eccentricity of a vertex v is defined as the greatest distance from v to any other vertex. A center of a graph is a vertex with minimal eccentricity. A graph...
or bicentered
Centered tree
In discrete mathematics, a centered tree is a tree with only one center, and a bicentered tree is a tree with two centers.Given a graph, the eccentricity of a vertex v is defined as the greatest distance from v to any other vertex. A center of a graph is a vertex with minimal eccentricity. A graph...
.
As opposed to these examples, not all vertex separators are balanced, but that property is most useful for applications in computer science, such as the planar separator theorem
Planar separator theorem
In graph theory, the planar separator theorem is a form of isoperimetric inequality for planar graphs, that states that any planar graph can be split into smaller pieces by removing a small number of vertices...
.
Minimal separators
Let S be an (a,b)-separator, that is, a vertex subset that separates two nonadjacent vertices a and b. Then S is a minimal (a,b)-separator if no proper subset of S separates a and b. More generally, S is called a minimal separator if it is a minimal separator for some pair (a,b) of nonadjacent vertices. The following is a well-known result characterizing the minimal separators:Lemma. A vertex separator S in G is minimal if and only if the graph
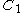, obtained by removing S from G, has two connected components and 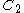such that each vertex in S is both adjacent to some vertex in 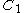and to some vertex in .The minimal separators also form an algebraic structure
Algebraic structure
In abstract algebra, an algebraic structure consists of one or more sets, called underlying sets or carriers or sorts, closed under one or more operations, satisfying some axioms. Abstract algebra is primarily the study of algebraic structures and their properties...
: For two fixed vertices a and b of a given graph G, an (a,b)-separator S can be regarded as a predecessor of another (a,b)-separator T, if every path from a to b meets S before it meets T. More rigorously, the predecessor relation is defined as follows: Let S and T be two (a,b)-separators in 'G'. Then S is a predecessor of T, in symbols
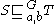, if for each 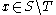, every path connecting x to b meets T. It follows from the definition that the predecessor relation yields a preorderPreorder
In mathematics, especially in order theory, preorders are binary relations that are reflexive and transitive.For example, all partial orders and equivalence relations are preorders...
on the set of all (a,b)-separators. Furthermore, proved that the predecessor relation gives rise to a complete lattice
Complete lattice
In mathematics, a complete lattice is a partially ordered set in which all subsets have both a supremum and an infimum . Complete lattices appear in many applications in mathematics and computer science...
when restricted to the set of minimal (a,b)-separators in G.