.gif)
Cardinal point (optics)
Encyclopedia
In Gaussian optics
, the cardinal points consist of three pairs of points
located on the optical axis
of an ideal, rotationally symmetric, focal, optical system. For ideal systems, the basic imaging properties (e.g., image size, location, and orientation) are completely determined by the locations of the cardinal points; in fact only four points are necessary: the focal points and either the principal or nodal points. However, the only ideal system that has been achieved in practice is the plane mirror
. Consequently, the practical utility of cardinal points would be very limited. However, the cardinal points are widely used to approximate the behavior of real rotationally symmetric, focal, systems.
The three pairs of cardinal points are:
for each ray
entering an optical system a single, unique, ray exits. In mathematical terms, the optical system simply performs a transformation mapping any object ray to an image ray. The object ray and its associated image ray are called conjugates; one can say that the image ray is conjugate to its corresponding object ray or vice versa. This term also applies to corresponding pairs of object and image points and planes.
associated with a refractive index
. The analysis of optical systems is greatly simplified by the use of optical spaces which enable designers to place the origin of a coordinate system at any of several convenient locations. In the design of optical systems two optical spaces, object space and image space, are always employed. Additional intermediate spaces are often used as well.
Optical spaces extend to infinity in all directions. The object space does not exist only on the "input" side of the system, nor the image space only on the "output" side. All optical spaces thus overlap completely. Typically, the origin and at least some of the coordinate axes of each space are different. It may not be possible to discern from an illustration to which space a point, ray, or plane belongs unless some convention is adopted. A common convention uses capital letters to label points and lower case letters to indicate distances. Unprimed letters indicate object space and primed letters image space. Intermediate spaces are indicated by additional primes. The same letter is used to indicate a conjugate relationship either between points or distances. The only exception is the use of F and F' to indicate respectively object and image space focal points (which are not conjugate). The term "object point" does not necessarily refer to a point on a specific object but rather to a point in object space; similarly for "image point".
One may wonder how an object point can exist on the "output" side of an optical system or conversely how an image point could be located on the "input" side of an optical system. The answer in both cases is that the points are virtual. Optical spaces are divided into real and virtual parts. Thus, an object point on the "output" side of the system is in the virtual part of object space and is referred to as a virtual object point. Object points on the "input" side are in the real part of object space and are real object points. The situation is reversed for image points.
It is common practice to designate the horizontal axis of an optical space as the z-axis with the positive direction left to right. Similarly, the y-axis is vertical with the positive direction upward.
, or simply "the axis". Any point on the axis (in any space) is an axial point.
Rotational symmetry greatly simplifies the analysis of optical systems, which otherwise must be analyzed in three dimensions. Rotational symmetry allows the system to be analyzed by considering only rays confined to a single transverse plane containing the optical axis. Such a plane is called a meridional plane; it is a cross-section
through the system.
It is common practice to place the horizontal axes of both object and image space on the optical axis, so the z-axis, z'-axis and optical axis all overlap. However, in general the origins of object and image space do not conincide but are located at different positions along the optical axis. Likewise, the y and y' axes of object and image space do not overlap.
In some optical systems imaging is stigmatic for one or perhaps a few object points, but to be an ideal system imaging must be stigmatic for every object point. The word originating is in quotes because in geometrical optics the term ray is not used in quite the same way as mathematicians typically use the term in geometry
. In mathematics a line extends infinitely in both directions but a ray extends infinitely in one direction with a definite terminus in the other direction. In optics a ray extends infinitely in both directions so it is analogous to a geometrical line. In stigmatic imaging an object ray intersecting any specific point, A, in object space must be conjugate to an image ray intersecting the conjugate point A' in image space. A consequence is that every point on an object ray is necessarily conjugate to some point on the conjugate image ray.
Geometrical similarity implies the image is a scale model of the object. There is no restriction on the image's orientation. The image may be inverted or otherwise rotated with respect to the object.
 The cardinal points lie on the optical axis
The cardinal points lie on the optical axis
of the optical system. Each point is defined by the effect the optical system has on rays
that pass through that point, in the paraxial approximation
. The paraxial approximation assumes that rays travel at shallow angles with respect to the optical axis, so that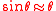 and
and 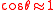 . Aperture effects are ignored: rays that do not pass through the aperture stop of the system are not considered in the discussion below.
. Aperture effects are ignored: rays that do not pass through the aperture stop of the system are not considered in the discussion below.
 The front and rear (or back) focal planes are defined as the planes, perpendicular to the optic axis, which pass through the front and rear focal points. An object infinitely far from the optical system forms an image
The front and rear (or back) focal planes are defined as the planes, perpendicular to the optic axis, which pass through the front and rear focal points. An object infinitely far from the optical system forms an image
at the rear focal plane. For objects a finite distance away, the image is formed at a different location, but rays that leave the object parallel to one another cross at the rear focal plane.
 A diaphragm
A diaphragm
or "stop" at the rear focal plane can be used to filter rays by angle, since:
Note that the aperture must be centered on the optical axis for this to work as indicated. Using a sufficiently small aperture in the focal plane will make the lens telecentric
.
Similarly, the allowed range of angles on the output side of the lens can be filtered by putting an aperture at the front focal plane of the lens (or a lens group within the overall lens). This is important for DSLR cameras having CCD
sensors. The pixels in these sensors are more sensitive to rays that hit them straight on than to those that strike at an angle. A lens that does not control the angle of incidence at the detector will produce pixel vignetting in the images.
of the system. The principal points are the points where the principal planes cross the optical axis.
If the medium surrounding the optical system has a refractive index
of 1 (e.g., air or vacuum
), then the distance from the principal planes to their corresponding focal points is just the focal length
of the system. In the more general case, the distance to the foci is the focal length multiplied by the index of refraction of the medium.
For a thin lens
in air, the principal planes both lie at the location of the lens. The point where they cross the optical axis is sometimes misleadingly called the optical centre of the lens. Note, however, that for a real lens the principal planes do not necessarily pass through the centre of the lens, and in general may not lie inside the lens at all.
In anatomy
, the surface vertices of the eye's lens
are called the anterior and posterior poles of the lens.
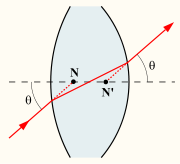 The front and rear nodal points have the property that a ray aimed at one of them will be refracted by the lens such that it appears to have come from the other, and with the same angle with respect to the optical axis. The nodal points therefore do for angles what the principal planes do for transverse distance. If the medium on both sides of the optical system is the same (e.g., air), then the front and rear nodal points coincide with the front and rear principal points, respectively.
The front and rear nodal points have the property that a ray aimed at one of them will be refracted by the lens such that it appears to have come from the other, and with the same angle with respect to the optical axis. The nodal points therefore do for angles what the principal planes do for transverse distance. If the medium on both sides of the optical system is the same (e.g., air), then the front and rear nodal points coincide with the front and rear principal points, respectively.
The nodal points are widely misunderstood in photography
, where it is commonly asserted that the light rays "intersect" at "the nodal point", that the iris diaphragm of the lens is located there, and that this is the correct pivot point for panoramic photography
, so as to avoid parallax
error. These claims generally arise from confusion about the optics of camera lenses, as well as confusion between the nodal points and the other cardinal points of the system. (A better choice of the point about which to pivot a camera for panoramic photography can be shown to be the centre of the system's entrance pupil
. On the other hand, swing-lens cameras with fixed film position rotate the lens about the rear nodal point to stabilize the image on the film.)
Gaussian optics
Gaussian optics is a technique in geometrical optics that describes the behaviour of light rays in optical systems by using the paraxial approximation, in which only rays which make small angles with the optical axis of the system are considered. In this approximation, trigonometric functions can...
, the cardinal points consist of three pairs of points
Point (geometry)
In geometry, topology and related branches of mathematics a spatial point is a primitive notion upon which other concepts may be defined. In geometry, points are zero-dimensional; i.e., they do not have volume, area, length, or any other higher-dimensional analogue. In branches of mathematics...
located on the optical axis
Optical axis
An optical axis is a line along which there is some degree of rotational symmetry in an optical system such as a camera lens or microscope.The optical axis is an imaginary line that defines the path along which light propagates through the system...
of an ideal, rotationally symmetric, focal, optical system. For ideal systems, the basic imaging properties (e.g., image size, location, and orientation) are completely determined by the locations of the cardinal points; in fact only four points are necessary: the focal points and either the principal or nodal points. However, the only ideal system that has been achieved in practice is the plane mirror
Plane mirror
A plane mirror is a mirror with a plane reflective surface.For light rays striking a plane mirror, the angle of reflection equals the angle of incidence...
. Consequently, the practical utility of cardinal points would be very limited. However, the cardinal points are widely used to approximate the behavior of real rotationally symmetric, focal, systems.
The three pairs of cardinal points are:
- The focal pointsFocus (optics)In geometrical optics, a focus, also called an image point, is the point where light rays originating from a point on the object converge. Although the focus is conceptually a point, physically the focus has a spatial extent, called the blur circle. This non-ideal focusing may be caused by...
- The principal points
- The nodal points
Modeling optical systems as mathematical transformations
In geometrical opticsGeometrical optics
Geometrical optics, or ray optics, describes light propagation in terms of "rays". The "ray" in geometric optics is an abstraction, or "instrument", which can be used to approximately model how light will propagate. Light rays are defined to propagate in a rectilinear path as far as they travel in...
for each ray
Ray (optics)
In optics, a ray is an idealized narrow beam of light. Rays are used to model the propagation of light through an optical system, by dividing the real light field up into discrete rays that can be computationally propagated through the system by the techniques of ray tracing. This allows even very...
entering an optical system a single, unique, ray exits. In mathematical terms, the optical system simply performs a transformation mapping any object ray to an image ray. The object ray and its associated image ray are called conjugates; one can say that the image ray is conjugate to its corresponding object ray or vice versa. This term also applies to corresponding pairs of object and image points and planes.
Optical spaces
Optical spaces facilitate the modeling of optical systems as mathematical transformations. An optical space is a mathematical coordinate system such as a Cartesian coordinate systemCartesian coordinate system
A Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
associated with a refractive index
Refractive index
In optics the refractive index or index of refraction of a substance or medium is a measure of the speed of light in that medium. It is expressed as a ratio of the speed of light in vacuum relative to that in the considered medium....
. The analysis of optical systems is greatly simplified by the use of optical spaces which enable designers to place the origin of a coordinate system at any of several convenient locations. In the design of optical systems two optical spaces, object space and image space, are always employed. Additional intermediate spaces are often used as well.
Optical spaces extend to infinity in all directions. The object space does not exist only on the "input" side of the system, nor the image space only on the "output" side. All optical spaces thus overlap completely. Typically, the origin and at least some of the coordinate axes of each space are different. It may not be possible to discern from an illustration to which space a point, ray, or plane belongs unless some convention is adopted. A common convention uses capital letters to label points and lower case letters to indicate distances. Unprimed letters indicate object space and primed letters image space. Intermediate spaces are indicated by additional primes. The same letter is used to indicate a conjugate relationship either between points or distances. The only exception is the use of F and F' to indicate respectively object and image space focal points (which are not conjugate). The term "object point" does not necessarily refer to a point on a specific object but rather to a point in object space; similarly for "image point".
One may wonder how an object point can exist on the "output" side of an optical system or conversely how an image point could be located on the "input" side of an optical system. The answer in both cases is that the points are virtual. Optical spaces are divided into real and virtual parts. Thus, an object point on the "output" side of the system is in the virtual part of object space and is referred to as a virtual object point. Object points on the "input" side are in the real part of object space and are real object points. The situation is reversed for image points.
It is common practice to designate the horizontal axis of an optical space as the z-axis with the positive direction left to right. Similarly, the y-axis is vertical with the positive direction upward.
Rotationally symmetric optical systems; Optical axis, axial points, and meridional planes
An optical system is rotationally symmetric if its imaging properties are unchanged by any rotation about some axis. Occasionally, an optical system is folded using plane mirrors. An optical system is considered rotationally symmetric if it possesses rotational symmetry when unfolded. The (unique) axis of rotational symmetry is the optical axisOptical axis
An optical axis is a line along which there is some degree of rotational symmetry in an optical system such as a camera lens or microscope.The optical axis is an imaginary line that defines the path along which light propagates through the system...
, or simply "the axis". Any point on the axis (in any space) is an axial point.
Rotational symmetry greatly simplifies the analysis of optical systems, which otherwise must be analyzed in three dimensions. Rotational symmetry allows the system to be analyzed by considering only rays confined to a single transverse plane containing the optical axis. Such a plane is called a meridional plane; it is a cross-section
Cross section (geometry)
In geometry, a cross-section is the intersection of a figure in 2-dimensional space with a line, or of a body in 3-dimensional space with a plane, etc...
through the system.
It is common practice to place the horizontal axes of both object and image space on the optical axis, so the z-axis, z'-axis and optical axis all overlap. However, in general the origins of object and image space do not conincide but are located at different positions along the optical axis. Likewise, the y and y' axes of object and image space do not overlap.
Ideal, rotationally symmetric, optical imaging system
An ideal, rotationally symmetric, optical imaging system must meet three criteria:- All rays "originating" from any object point converge to a single image point (Imaging is stigmatic).
- Object planes perpendicular to the optical axis are conjugate to image planes perpendicular to the axis.
- The image of an object confined to a plane normal to the axis is geometrically similar to the object.
In some optical systems imaging is stigmatic for one or perhaps a few object points, but to be an ideal system imaging must be stigmatic for every object point. The word originating is in quotes because in geometrical optics the term ray is not used in quite the same way as mathematicians typically use the term in geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
. In mathematics a line extends infinitely in both directions but a ray extends infinitely in one direction with a definite terminus in the other direction. In optics a ray extends infinitely in both directions so it is analogous to a geometrical line. In stigmatic imaging an object ray intersecting any specific point, A, in object space must be conjugate to an image ray intersecting the conjugate point A' in image space. A consequence is that every point on an object ray is necessarily conjugate to some point on the conjugate image ray.
Geometrical similarity implies the image is a scale model of the object. There is no restriction on the image's orientation. The image may be inverted or otherwise rotated with respect to the object.
Focal and afocal systems, focal points
In afocal systems an object ray parallel to the optical axis is conjugate to an image ray parallel to the optical axis. Such systems have no focal points (hence afocal) and also lack principal and nodal points. The system is focal if an object ray parallel to the axis is conjugate to an image ray that intersects the optical axis. The intersection of the image ray with the optical axis is the focal point in image space F'. Focal systems also have an axial object point F such that any ray intersecting is conjugate to a ray parallel to the optical axis. F is the object space focal point of the system.Detailed explanations

Optical axis
An optical axis is a line along which there is some degree of rotational symmetry in an optical system such as a camera lens or microscope.The optical axis is an imaginary line that defines the path along which light propagates through the system...
of the optical system. Each point is defined by the effect the optical system has on rays
Ray (optics)
In optics, a ray is an idealized narrow beam of light. Rays are used to model the propagation of light through an optical system, by dividing the real light field up into discrete rays that can be computationally propagated through the system by the techniques of ray tracing. This allows even very...
that pass through that point, in the paraxial approximation
Paraxial approximation
In geometric optics, the paraxial approximation is a small-angle approximation used in Gaussian optics and ray tracing of light through an optical system ....
. The paraxial approximation assumes that rays travel at shallow angles with respect to the optical axis, so that
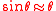 and
and 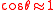 . Aperture effects are ignored: rays that do not pass through the aperture stop of the system are not considered in the discussion below.
. Aperture effects are ignored: rays that do not pass through the aperture stop of the system are not considered in the discussion below.Focal planes
The front focal point of an optical system, by definition, has the property that any ray that passes through it will emerge from the system parallel to the optical axis. The rear (or back) focal point of the system has the reverse property: rays that enter the system parallel to the optical axis are focused such that they pass through the rear focal point.
Image
An image is an artifact, for example a two-dimensional picture, that has a similar appearance to some subject—usually a physical object or a person.-Characteristics:...
at the rear focal plane. For objects a finite distance away, the image is formed at a different location, but rays that leave the object parallel to one another cross at the rear focal plane.

Diaphragm (optics)
In optics, a diaphragm is a thin opaque structure with an opening at its center. The role of the diaphragm is to stop the passage of light, except for the light passing through the aperture...
or "stop" at the rear focal plane can be used to filter rays by angle, since:
- It only allows rays to pass that are emitted at an angle (relative to the optical axisOptical axisAn optical axis is a line along which there is some degree of rotational symmetry in an optical system such as a camera lens or microscope.The optical axis is an imaginary line that defines the path along which light propagates through the system...
) that is sufficiently small. (An infinitely small aperture would only allow rays that are emitted along the optical axis to pass.) - No matter where on the object the ray comes from, the ray will pass through the aperture as long as the angle at which it is emitted from the object is small enough.
Note that the aperture must be centered on the optical axis for this to work as indicated. Using a sufficiently small aperture in the focal plane will make the lens telecentric
Telecentric lens
A telecentric lens is a compound lens which has its entrance or exit pupil at infinity; in the prior case, this produces an orthographic view of the subject. This means that the chief rays are parallel to the optical axis in front of or behind the system, respectively...
.
Similarly, the allowed range of angles on the output side of the lens can be filtered by putting an aperture at the front focal plane of the lens (or a lens group within the overall lens). This is important for DSLR cameras having CCD
Charge-coupled device
A charge-coupled device is a device for the movement of electrical charge, usually from within the device to an area where the charge can be manipulated, for example conversion into a digital value. This is achieved by "shifting" the signals between stages within the device one at a time...
sensors. The pixels in these sensors are more sensitive to rays that hit them straight on than to those that strike at an angle. A lens that does not control the angle of incidence at the detector will produce pixel vignetting in the images.
Principal planes and points
The two principal planes have the property that a ray emerging from the lens appears to have crossed the rear principal plane at the same distance from the axis that that ray appeared to cross the front principal plane, as viewed from the front of the lens. This means that the lens can be treated as if all of the refraction happened at the principal planes. The principal planes are crucial in defining the optical properties of the system, since it is the distance of the object and image from the front and rear principal planes that determines the magnificationMagnification
Magnification is the process of enlarging something only in appearance, not in physical size. This enlargement is quantified by a calculated number also called "magnification"...
of the system. The principal points are the points where the principal planes cross the optical axis.
If the medium surrounding the optical system has a refractive index
Refractive index
In optics the refractive index or index of refraction of a substance or medium is a measure of the speed of light in that medium. It is expressed as a ratio of the speed of light in vacuum relative to that in the considered medium....
of 1 (e.g., air or vacuum
Vacuum
In everyday usage, vacuum is a volume of space that is essentially empty of matter, such that its gaseous pressure is much less than atmospheric pressure. The word comes from the Latin term for "empty". A perfect vacuum would be one with no particles in it at all, which is impossible to achieve in...
), then the distance from the principal planes to their corresponding focal points is just the focal length
Focal length
The focal length of an optical system is a measure of how strongly the system converges or diverges light. For an optical system in air, it is the distance over which initially collimated rays are brought to a focus...
of the system. In the more general case, the distance to the foci is the focal length multiplied by the index of refraction of the medium.
For a thin lens
Thin lens
[Image:Lens1.svg|thumb|A lens can be considered a thin lens if d [Image:Lens1.svg|thumb|A lens can be considered a thin lens if d [Image:Lens1.svg|thumb|A lens can be considered a thin lens if d...
in air, the principal planes both lie at the location of the lens. The point where they cross the optical axis is sometimes misleadingly called the optical centre of the lens. Note, however, that for a real lens the principal planes do not necessarily pass through the centre of the lens, and in general may not lie inside the lens at all.
Surface vertices
The surface vertices are the points where each surface crosses the optical axis. They are important primarily because they are the physically measurable parameters for the position of the optical elements, and so the positions of the other cardinal points must be known with respect to the vertices to describe the physical system.In anatomy
Anatomy
Anatomy is a branch of biology and medicine that is the consideration of the structure of living things. It is a general term that includes human anatomy, animal anatomy , and plant anatomy...
, the surface vertices of the eye's lens
Lens (anatomy)
The crystalline lens is a transparent, biconvex structure in the eye that, along with the cornea, helps to refract light to be focused on the retina. The lens, by changing shape, functions to change the focal distance of the eye so that it can focus on objects at various distances, thus allowing a...
are called the anterior and posterior poles of the lens.
Nodal points

The nodal points are widely misunderstood in photography
Photography
Photography is the art, science and practice of creating durable images by recording light or other electromagnetic radiation, either electronically by means of an image sensor or chemically by means of a light-sensitive material such as photographic film...
, where it is commonly asserted that the light rays "intersect" at "the nodal point", that the iris diaphragm of the lens is located there, and that this is the correct pivot point for panoramic photography
Panoramic photography
Panoramic photography is a technique of photography, using specialized equipment or software, that captures images with elongated fields of view. It is sometimes known as wide format photography. The term has also been applied to a photograph that is cropped to a relatively wide aspect ratio...
, so as to avoid parallax
Parallax
Parallax is a displacement or difference in the apparent position of an object viewed along two different lines of sight, and is measured by the angle or semi-angle of inclination between those two lines. The term is derived from the Greek παράλλαξις , meaning "alteration"...
error. These claims generally arise from confusion about the optics of camera lenses, as well as confusion between the nodal points and the other cardinal points of the system. (A better choice of the point about which to pivot a camera for panoramic photography can be shown to be the centre of the system's entrance pupil
Entrance pupil
In an optical system, the entrance pupil is the optical image of the physical aperture stop, as 'seen' through the front of the lens system. The corresponding image of the aperture as seen through the back of the lens system is called the exit pupil...
. On the other hand, swing-lens cameras with fixed film position rotate the lens about the rear nodal point to stabilize the image on the film.)
See also
- Film planeFilm planeA film plane is the area inside any image taking device with a lens and a digital sensor or film; such as a camera. The film plane varies in distance from the lens focal point in each manufacturer...
- Pinhole camera modelPinhole camera modelThe pinhole camera model describes the mathematical relationship between the coordinates of a 3D point and its projection onto the image plane of an ideal pinhole camera, where the camera aperture is described as a point and no lenses are used to focus light...
- Radius of curvature (optics)Radius of curvature (optics)Radius of curvature has specific meaning and sign convention in optical design. A spherical lens or mirror surface has a center of curvature located in either along or decentered from the system local optical axis. The vertex of the lens surface is located on the local optical axis...
- Vergence (optics)Vergence (optics)The vergence of a light bundle in optics is the reciprocal of the distance between the point of focus and a reference plane. It is measured in dioptres . Vergence can also be understood as a measure of the curvature of the optical wavefront...

