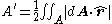Cross section (geometry)
Encyclopedia
In geometry
, a cross-section is the intersection
of a figure in 2-dimensional space with a line, or of a body in 3-dimensional space with a plane, etc. More plainly, when cutting an object into slices one gets many parallel cross-sections.
Cavalieri's principle
states that solids with corresponding cross-sections of equal areas have equal volumes.
The cross-sectional area ( ) of an object when viewed from a particular angle is the total area of the orthographic projection of the object from that angle. For example, a cylinder of height h and radius r has
) of an object when viewed from a particular angle is the total area of the orthographic projection of the object from that angle. For example, a cylinder of height h and radius r has  when viewed along its central axis, and
when viewed along its central axis, and 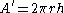 when viewed from an orthogonal direction. A sphere of radius r has
when viewed from an orthogonal direction. A sphere of radius r has  when viewed from any angle. More generically,
when viewed from any angle. More generically,  can be calculated by evaluating the following surface integral:
can be calculated by evaluating the following surface integral:
where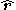 is a unit vector pointing along the viewing direction toward the viewer,
is a unit vector pointing along the viewing direction toward the viewer, 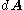 is a surface element with outward-pointing normal, and the integral is taken only over the top-most surface, that part of the surface that is "visible" from the perspective of the viewer. For a convex body
is a surface element with outward-pointing normal, and the integral is taken only over the top-most surface, that part of the surface that is "visible" from the perspective of the viewer. For a convex body
, each ray through the object from the viewer's perspective crosses just two surfaces. For such objects, the integral may be taken over the entire surface (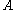 ) by taking the absolute value of the integrand (so that the "top" and "bottom" of the object do not subtract away, as would be required by the Divergence Theorem
) by taking the absolute value of the integrand (so that the "top" and "bottom" of the object do not subtract away, as would be required by the Divergence Theorem
applied to the constant vector field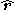 ) and dividing by two:
) and dividing by two:
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, a cross-section is the intersection
Intersection (set theory)
In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B , but no other elements....
of a figure in 2-dimensional space with a line, or of a body in 3-dimensional space with a plane, etc. More plainly, when cutting an object into slices one gets many parallel cross-sections.
Cavalieri's principle
Cavalieri's principle
In geometry, Cavalieri's principle, sometimes called the method of indivisibles, named after Bonaventura Cavalieri, is as follows:* 2-dimensional case: Suppose two regions in a plane are included between two parallel lines in that plane...
states that solids with corresponding cross-sections of equal areas have equal volumes.
The cross-sectional area (
 ) of an object when viewed from a particular angle is the total area of the orthographic projection of the object from that angle. For example, a cylinder of height h and radius r has
) of an object when viewed from a particular angle is the total area of the orthographic projection of the object from that angle. For example, a cylinder of height h and radius r has  when viewed along its central axis, and
when viewed along its central axis, and 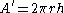 when viewed from an orthogonal direction. A sphere of radius r has
when viewed from an orthogonal direction. A sphere of radius r has  when viewed from any angle. More generically,
when viewed from any angle. More generically,  can be calculated by evaluating the following surface integral:
can be calculated by evaluating the following surface integral:where
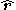 is a unit vector pointing along the viewing direction toward the viewer,
is a unit vector pointing along the viewing direction toward the viewer, 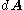 is a surface element with outward-pointing normal, and the integral is taken only over the top-most surface, that part of the surface that is "visible" from the perspective of the viewer. For a convex body
is a surface element with outward-pointing normal, and the integral is taken only over the top-most surface, that part of the surface that is "visible" from the perspective of the viewer. For a convex bodyConvex body
In mathematics, a convex body in n-dimensional Euclidean space Rn is a compact convex set with non-empty interior.A convex body K is called symmetric if it is centrally symmetric with respect to the origin, i.e. a point x lies in K if and only if its antipode, −x, also lies in K...
, each ray through the object from the viewer's perspective crosses just two surfaces. For such objects, the integral may be taken over the entire surface (
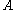 ) by taking the absolute value of the integrand (so that the "top" and "bottom" of the object do not subtract away, as would be required by the Divergence Theorem
) by taking the absolute value of the integrand (so that the "top" and "bottom" of the object do not subtract away, as would be required by the Divergence TheoremDivergence theorem
In vector calculus, the divergence theorem, also known as Gauss' theorem , Ostrogradsky's theorem , or Gauss–Ostrogradsky theorem is a result that relates the flow of a vector field through a surface to the behavior of the vector field inside the surface.More precisely, the divergence theorem...
applied to the constant vector field
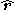 ) and dividing by two:
) and dividing by two:See also
- Descriptive geometryDescriptive geometryDescriptive geometry is the branch of geometry which allows the representation of three-dimensional objects in two dimensions, by using a specific set of procedures. The resulting techniques are important for engineering, architecture, design and in art...
- Exploded view drawing
- Graphical projectionGraphical projectionGraphical projection is a protocol by which an image of a three-dimensional object is projected onto a planar surface without the aid of mathematical calculation, used in technical drawing.- Overview :...
- Plans (drawings)Plans (drawings)Plans are a set of drawings or two-dimensional diagrams used to describe a place or object, or to communicate building or fabrication instructions. Usually plans are drawn or printed on paper, but they can take the form of a digital file.- Overview :...