
Radius of curvature (optics)
Encyclopedia
Radius of curvature has specific meaning and sign convention
in optical design. A spherical lens
or mirror
surface has a center of curvature
located in (x, y, z) either along or decentered from the system local optical axis
. The vertex of the lens surface is located on the local optical axis. The distance from the vertex to the center of curvature is the radius of curvature
of the surface. The sign convention for the optical radius of curvature is as follows:
Thus when viewing a biconvex lens from the side, the left surface radius of curvature is positive, and the right surface has a negative radius of curvature.
Note however that in areas of optics other than design, other sign conventions are sometimes used. In particular, many undergraduate physics textbooks use an alternate sign convention in which convex surfaces of lenses are always positive. Care should be taken when using formulas taken from different sources.
es, also have a radius of curvature. These surfaces are typically designed such that their profile is described by the equation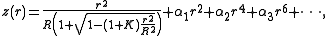
where the optic axis is presumed to lie in the z direction, and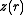 is the sag—the z-component of the displacement
is the sag—the z-component of the displacement
of the surface from the vertex, at distance from the axis. If
from the axis. If 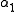 and
and 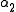 are zero, then
are zero, then 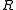 is the radius of curvature and
is the radius of curvature and 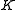 is the conic constant
is the conic constant
, as measured at the vertex (where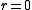 ). The coefficients
). The coefficients 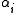 describe the deviation of the surface from the axially symmetric
describe the deviation of the surface from the axially symmetric
quadric surface specified by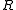 and
and 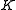 .
.
Sign convention
In physics, a sign convention is a choice of the physical significance of signs for a set of quantities, in a case where the choice of sign is arbitrary. "Arbitrary" here means that the same physical system can be correctly described using different choices for the signs, as long as one set of...
in optical design. A spherical lens
Lens (optics)
A lens is an optical device with perfect or approximate axial symmetry which transmits and refracts light, converging or diverging the beam. A simple lens consists of a single optical element...
or mirror
Mirror
A mirror is an object that reflects light or sound in a way that preserves much of its original quality prior to its contact with the mirror. Some mirrors also filter out some wavelengths, while preserving other wavelengths in the reflection...
surface has a center of curvature
Center of curvature
In geometry, center of curvature of a curve is found at a point that is at a distance equal to the radius of curvature lying on the normal vector. It is the point at infinity if the curvature is zero. The osculating circle to the curve is centered at the center of curvature....
located in (x, y, z) either along or decentered from the system local optical axis
Optical axis
An optical axis is a line along which there is some degree of rotational symmetry in an optical system such as a camera lens or microscope.The optical axis is an imaginary line that defines the path along which light propagates through the system...
. The vertex of the lens surface is located on the local optical axis. The distance from the vertex to the center of curvature is the radius of curvature
Radius
In classical geometry, a radius of a circle or sphere is any line segment from its center to its perimeter. By extension, the radius of a circle or sphere is the length of any such segment, which is half the diameter. If the object does not have an obvious center, the term may refer to its...
of the surface. The sign convention for the optical radius of curvature is as follows:
- If the vertex lies to the left of the center of curvature, the radius of curvature is positive.
- If the vertex lies to the right of the center of curvature, the radius of curvature is negative.
Thus when viewing a biconvex lens from the side, the left surface radius of curvature is positive, and the right surface has a negative radius of curvature.
Note however that in areas of optics other than design, other sign conventions are sometimes used. In particular, many undergraduate physics textbooks use an alternate sign convention in which convex surfaces of lenses are always positive. Care should be taken when using formulas taken from different sources.
Aspheric surfaces
Optical surfaces with non-spherical profiles, such as the surfaces of aspheric lensAspheric lens
An aspheric lens or asphere is a lens whose surface profiles are not portions of a sphere or cylinder. In photography, a lens assembly that includes an aspheric element is often called an aspherical lens....
es, also have a radius of curvature. These surfaces are typically designed such that their profile is described by the equation
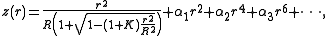
where the optic axis is presumed to lie in the z direction, and
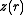 is the sag—the z-component of the displacement
is the sag—the z-component of the displacementDisplacement (vector)
A displacement is the shortest distance from the initial to the final position of a point P. Thus, it is the length of an imaginary straight path, typically distinct from the path actually travelled by P...
of the surface from the vertex, at distance
 from the axis. If
from the axis. If 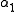 and
and 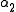 are zero, then
are zero, then 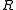 is the radius of curvature and
is the radius of curvature and 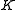 is the conic constant
is the conic constantConic constant
In geometry, the conic constant is a quantity describing conic sections, and is represented by the letter K...
, as measured at the vertex (where
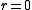 ). The coefficients
). The coefficients 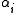 describe the deviation of the surface from the axially symmetric
describe the deviation of the surface from the axially symmetricAxial symmetry
Axial symmetry is symmetry around an axis; an object is axially symmetric if its appearance is unchanged if rotated around an axis . For example, a baseball bat or a tea saucer looks the same if it is rotated by any angle about the line passing lengthwise through its center, so it is axially...
quadric surface specified by
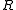 and
and 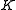 .
.See also
- Radius of curvature (applications)
- RadiusRadiusIn classical geometry, a radius of a circle or sphere is any line segment from its center to its perimeter. By extension, the radius of a circle or sphere is the length of any such segment, which is half the diameter. If the object does not have an obvious center, the term may refer to its...
- Base curve radiusBase curve radiusBase curve radius or simply base curve, abbreviated BCR or BC, is the measure of one important parameter of a lens in optometry. On a spectacle lens, it is the flatter curvature of the front surface and on a contact lens it is the curvature of the back surface. Typical values for a contact lens are...
- Cardinal point (optics)Cardinal point (optics)In Gaussian optics, the cardinal points consist of three pairs of points located on the optical axis of an ideal, rotationally symmetric, focal, optical system...
- Vergence (optics)Vergence (optics)The vergence of a light bundle in optics is the reciprocal of the distance between the point of focus and a reference plane. It is measured in dioptres . Vergence can also be understood as a measure of the curvature of the optical wavefront...

