Capillary surface
Encyclopedia
In fluid mechanics
and mathematics
, a capillary surface is a surface
that represents the interface between two different fluid
s. As a consequence of being a surface
, a capillary surface has no thickness in slight contrast with most real fluid interfaces.
Capillary surfaces are of interest in mathematics because the problems involved are very nonlinear and have interesting properties, such as discontinuous dependence on boundary data at isolated points. In particular, static capillary surfaces with gravity absent have constant mean curvature
, so that a minimal surface
is a special case of static capillary surface.
They are also of practical interest for fluid management in space (or other environments free of body force
s), where both flow and static configuration are often dominated by capillary effects.
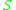, the equation reads
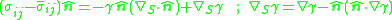
where
is the unit normal
pointing toward the "other" fluid (the one whose quantities are notated with bars),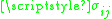
is the stress tensor (note that on the left is a tensor-vector product
),
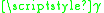is the surface tension
associated with the interface, and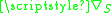
is the surface gradient
. Note that the quantity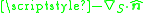
is twice the mean curvature
of the surface.
In fluid mechanics
, this equation serves as a boundary condition for interfacial flows, typically complementing the Navier–Stokes equations. It describes the discontinuity in stress
that is balanced by forces at the surface. As a boundary condition, it is somewhat unusual in that it introduces a new variable: the surface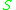
that defines the interface. It's not too surprising then that the stress balance equation normally mandates its own boundary conditions.
For best use, this vector equation is normally turned into 3 scalar equations via dot product with the unit normal and two selected unit tangents:
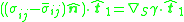
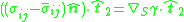
Note that the products lacking dots are tensor product
s of tensors with vectors (resulting in vectors similar to a matrix-vector product), those with dots are dot product
s. The first equation is called the normal stress equation, or the normal stress boundary condition. The second two equations are called tangential stress equations.
and pressure. Its actual form will depend on the specific fluid being dealt with, for the common case of incompressible Newtonian flow the stress tensor is given by
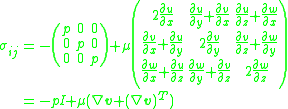
where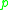
is the pressure
in the fluid,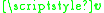
is the velocity, and 
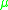is the viscosity
.
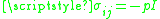, regardless of fluid type or compressibility. Considering the normal and tangential equations,
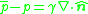
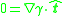
The first equation establishes that curvature forces are balanced by pressure forces. The second equation implies that a static interface cannot exist in the presence of nonzero surface tension gradient.
If gravity is the only body force
present, the Navier–Stokes equations simplify significantly:
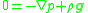
If coordinates are chosen so that gravity is nonzero only in the
direction, this equation degrades to a particularly simple form:
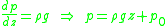
where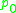
is an integration constant that represents some reference pressure at 
. Substituting this into the normal stress equation yields what is known as the Young-Laplace equation:
where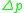
is the (constant) pressure difference across the interface, and 
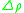is the difference in density
. Note that, since this equation defines a surface,
is the 
coordinate of the capillary surface. This nonlinear partial differential equation
when supplied with the right boundary conditions will define the static interface.
The pressure difference above is a constant, but its value will change if the
coordinate is shifted. The linear solution to pressure implies that, unless the gravity term is absent, it is always possible to define the 
coordinate so that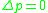 
. Nondimensionalized
, the Young-Laplace equation is usually studied in the form
where (if gravity is in the negative
direction) 
is positive if the denser fluid is "inside" the interface, negative if it is "outside", and zero if there is no gravity or if there is no difference in density between the fluids.
This nonlinear equation has some rich properties, especially in terms of existence of unique solutions. For example, the nonexistence of solution to some boundary value problem
implies that, physically, the problem can't be static. If a solution does exist, normally it'll exist for very specific values of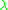
, which is representative of the pressure jump across the interface. This is interesting because there isn't another physical equation to determine the pressure difference. In a capillary tube, for example, implementing the contact angle boundary condition will yield a unique solution for exactly one value of 
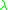. Solutions often aren't unique, this implies that there are multiple static interfaces possible; while they may all solve the same boundary value problem, the minimization of energy will normally favor one. Different solutions are called configurations of the interface.
that is imparted by surface tension:
where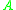
is the area of the surface being considered, and the total energy
is the summation of all energies. Note that every interface imparts energy. For example, if there are two different fluids (say liquid and gas) inside a solid container with gravity and other energy potentials absent, the energy of the system is
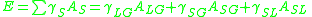
where the subscripts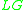
, 
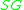, and 
respectively indicate the liquid–gas, solid–gas, and solid–liquid interfaces. Note that inclusion of gravity would require consideration of the volume enclosed by the capillary surface and the solid walls.
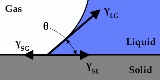
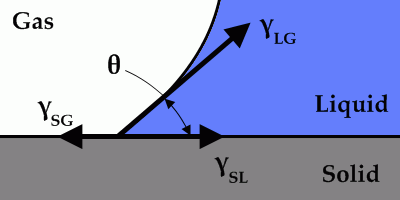Typically the surface tension values between the solid–gas and solid–liquid interfaces are not known. This does not pose a problem; since only changes in energy are of primary interest. If the net solid area 
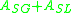is a constant, and the contact angle
is known, it may be shown that (again, for two different fluids in a solid container)
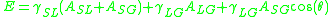
so that
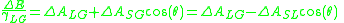
where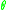
is the contact angle
and the capital delta indicates the change from one configuration to another. To obtain this result, it's necessary to sum (distributed) forces at the contact line (where solid, gas, and liquid meet) in a direction tangent to the solid interface and perpendicular to the contact line:
where the sum is zero because of the static
state. When solutions to the Young-Laplace equation aren't unique, the most physically favorable solution is the one of minimum energy, though experiments (especially low gravity) show that metastable surfaces can be surprisingly persistent, and that the most stable configuration can become metastable through mechanical jarring without too much difficulty. On the other hand, a metastable surface can sometimes spontaneously achieve lower energy without any input (seemingly at least) given enough time.
For static surfaces, the most common contact line boundary condition is the implementation of the contact angle
, which specifies the angle that one of the fluids meets the solid wall. The contact angle condition on the surface
is normally written as:
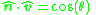
where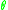
is the contact angle. This condition is imposed on the boundary (or boundaries) 
of the surface.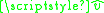 
is the unit outward normal to the solid surface, and 
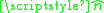is a unit normal to 
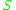. Choice of 
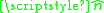depends on which fluid the contact angle is specified for.
For dynamic interfaces, the boundary condition showed above works well if the contact line velocity is low. If the velocity is high, the contact angle will change ("dynamic contact angle"), and as of 2007 the mechanics of the moving contact line (or even the validity of the contact angle as a parameter) is not known and an area of active research.
Fluid mechanics
Fluid mechanics is the study of fluids and the forces on them. Fluid mechanics can be divided into fluid statics, the study of fluids at rest; fluid kinematics, the study of fluids in motion; and fluid dynamics, the study of the effect of forces on fluid motion...
and mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a capillary surface is a surface
Surface
In mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...
that represents the interface between two different fluid
Fluid
In physics, a fluid is a substance that continually deforms under an applied shear stress. Fluids are a subset of the phases of matter and include liquids, gases, plasmas and, to some extent, plastic solids....
s. As a consequence of being a surface
Surface
In mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...
, a capillary surface has no thickness in slight contrast with most real fluid interfaces.
Capillary surfaces are of interest in mathematics because the problems involved are very nonlinear and have interesting properties, such as discontinuous dependence on boundary data at isolated points. In particular, static capillary surfaces with gravity absent have constant mean curvature
Mean curvature
In mathematics, the mean curvature H of a surface S is an extrinsic measure of curvature that comes from differential geometry and that locally describes the curvature of an embedded surface in some ambient space such as Euclidean space....
, so that a minimal surface
Minimal surface
In mathematics, a minimal surface is a surface with a mean curvature of zero.These include, but are not limited to, surfaces of minimum area subject to various constraints....
is a special case of static capillary surface.
They are also of practical interest for fluid management in space (or other environments free of body force
Body force
A body force is a force that acts throughout the volume of a body, in contrast to contact forces.Gravity and electromagnetic forces are examples of body forces. Centrifugal and Coriolis forces can also be viewed as body forces.This can be put into contrast to the classical definition of surface...
s), where both flow and static configuration are often dominated by capillary effects.
The stress balance equation
The defining equation for a capillary surface is called the stress balance equation, which can be derived by considering the forces and stresses acting on a small volume that is partly bounded by a capillary surface. For a fluid meeting another fluid (the "other" fluid notated with bars) at a surface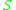, the equation reads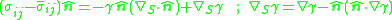where
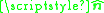is the unit normalSurface normal
A surface normal, or simply normal, to a flat surface is a vector that is perpendicular to that surface. A normal to a non-flat surface at a point P on the surface is a vector perpendicular to the tangent plane to that surface at P. The word "normal" is also used as an adjective: a line normal to a...
pointing toward the "other" fluid (the one whose quantities are notated with bars),
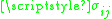is the stress tensor (note that on the left is a tensor-vector productTensor product
In mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
),
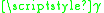is the surface tensionSurface tension
Surface tension is a property of the surface of a liquid that allows it to resist an external force. It is revealed, for example, in floating of some objects on the surface of water, even though they are denser than water, and in the ability of some insects to run on the water surface...
associated with the interface, and
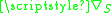is the surface gradientSurface gradient
In vector calculus, the surface gradient is a vector differential operator that is similar to the conventional gradient. The distinction is that the surface gradient takes effect along a surface....
. Note that the quantity
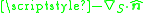is twice the mean curvatureMean curvature
In mathematics, the mean curvature H of a surface S is an extrinsic measure of curvature that comes from differential geometry and that locally describes the curvature of an embedded surface in some ambient space such as Euclidean space....
of the surface.
In fluid mechanics
Fluid mechanics
Fluid mechanics is the study of fluids and the forces on them. Fluid mechanics can be divided into fluid statics, the study of fluids at rest; fluid kinematics, the study of fluids in motion; and fluid dynamics, the study of the effect of forces on fluid motion...
, this equation serves as a boundary condition for interfacial flows, typically complementing the Navier–Stokes equations. It describes the discontinuity in stress
Stress (physics)
In continuum mechanics, stress is a measure of the internal forces acting within a deformable body. Quantitatively, it is a measure of the average force per unit area of a surface within the body on which internal forces act. These internal forces are a reaction to external forces applied on the body...
that is balanced by forces at the surface. As a boundary condition, it is somewhat unusual in that it introduces a new variable: the surface
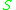that defines the interface. It's not too surprising then that the stress balance equation normally mandates its own boundary conditions.For best use, this vector equation is normally turned into 3 scalar equations via dot product with the unit normal and two selected unit tangents:
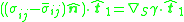
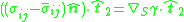
Note that the products lacking dots are tensor product
Tensor product
In mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
s of tensors with vectors (resulting in vectors similar to a matrix-vector product), those with dots are dot product
Dot product
In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
s. The first equation is called the normal stress equation, or the normal stress boundary condition. The second two equations are called tangential stress equations.
The stress tensor
The stress tensor is related to velocityVelocity
In physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...
and pressure. Its actual form will depend on the specific fluid being dealt with, for the common case of incompressible Newtonian flow the stress tensor is given by
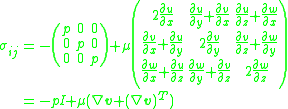
where
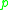is the pressurePressure
Pressure is the force per unit area applied in a direction perpendicular to the surface of an object. Gauge pressure is the pressure relative to the local atmospheric or ambient pressure.- Definition :...
in the fluid,
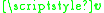is the velocity, and 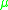is the viscosityViscosity
Viscosity is a measure of the resistance of a fluid which is being deformed by either shear or tensile stress. In everyday terms , viscosity is "thickness" or "internal friction". Thus, water is "thin", having a lower viscosity, while honey is "thick", having a higher viscosity...
.
Static interfaces
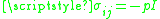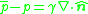
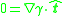
In the absence of motion, the stress tensors yield only hydrostatic pressure so that, regardless of fluid type or compressibility. Considering the normal and tangential equations,The first equation establishes that curvature forces are balanced by pressure forces. The second equation implies that a static interface cannot exist in the presence of nonzero surface tension gradient.
If gravity is the only body force
Body force
A body force is a force that acts throughout the volume of a body, in contrast to contact forces.Gravity and electromagnetic forces are examples of body forces. Centrifugal and Coriolis forces can also be viewed as body forces.This can be put into contrast to the classical definition of surface...
present, the Navier–Stokes equations simplify significantly:
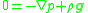
If coordinates are chosen so that gravity is nonzero only in the
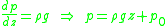
direction, this equation degrades to a particularly simple form:where
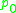is an integration constant that represents some reference pressure at . Substituting this into the normal stress equation yields what is known as the Young-Laplace equation:where
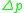is the (constant) pressure difference across the interface, and 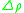is the difference in densityDensity
The mass density or density of a material is defined as its mass per unit volume. The symbol most often used for density is ρ . In some cases , density is also defined as its weight per unit volume; although, this quantity is more properly called specific weight...
. Note that, since this equation defines a surface,
is the coordinate of the capillary surface. This nonlinear partial differential equationPartial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
when supplied with the right boundary conditions will define the static interface.
The pressure difference above is a constant, but its value will change if the
coordinate is shifted. The linear solution to pressure implies that, unless the gravity term is absent, it is always possible to define the coordinate so that 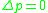. NondimensionalizedScale analysis
Scale analysis may refer to:* Scale analysis * Scale analysis...
, the Young-Laplace equation is usually studied in the form
where (if gravity is in the negative
direction) is positive if the denser fluid is "inside" the interface, negative if it is "outside", and zero if there is no gravity or if there is no difference in density between the fluids.This nonlinear equation has some rich properties, especially in terms of existence of unique solutions. For example, the nonexistence of solution to some boundary value problem
Boundary value problem
In mathematics, in the field of differential equations, a boundary value problem is a differential equation together with a set of additional restraints, called the boundary conditions...
implies that, physically, the problem can't be static. If a solution does exist, normally it'll exist for very specific values of
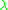, which is representative of the pressure jump across the interface. This is interesting because there isn't another physical equation to determine the pressure difference. In a capillary tube, for example, implementing the contact angle boundary condition will yield a unique solution for exactly one value of 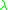. Solutions often aren't unique, this implies that there are multiple static interfaces possible; while they may all solve the same boundary value problem, the minimization of energy will normally favor one. Different solutions are called configurations of the interface.Energy consideration
A deep property of capillary surfaces is the surface energySurface energy
Surface energy quantifies the disruption of intermolecular bonds that occur when a surface is created. In the physics of solids, surfaces must be intrinsically less energetically favorable than the bulk of a material, otherwise there would be a driving force for surfaces to be created, removing...
that is imparted by surface tension:
where
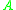is the area of the surface being considered, and the total energyEnergy
In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
is the summation of all energies. Note that every interface imparts energy. For example, if there are two different fluids (say liquid and gas) inside a solid container with gravity and other energy potentials absent, the energy of the system is
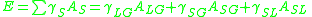
where the subscripts
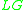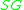, , and respectively indicate the liquid–gas, solid–gas, and solid–liquid interfaces. Note that inclusion of gravity would require consideration of the volume enclosed by the capillary surface and the solid walls. 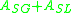is a constant, and the contact angleContact angle
The contact angle is the angle at which a liquid/vapor interface meets a solid surface. The contact angle is specific for any given system and is determined by the interactions across the three interfaces. Most often the concept is illustrated with a small liquid droplet resting on a flat...
is known, it may be shown that (again, for two different fluids in a solid container)
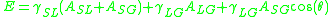
so that
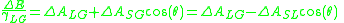
where
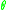is the contact angleContact angle
The contact angle is the angle at which a liquid/vapor interface meets a solid surface. The contact angle is specific for any given system and is determined by the interactions across the three interfaces. Most often the concept is illustrated with a small liquid droplet resting on a flat...
and the capital delta indicates the change from one configuration to another. To obtain this result, it's necessary to sum (distributed) forces at the contact line (where solid, gas, and liquid meet) in a direction tangent to the solid interface and perpendicular to the contact line:
where the sum is zero because of the static
Statics
Statics is the branch of mechanics concerned with the analysis of loads on physical systems in static equilibrium, that is, in a state where the relative positions of subsystems do not vary over time, or where components and structures are at a constant velocity...
state. When solutions to the Young-Laplace equation aren't unique, the most physically favorable solution is the one of minimum energy, though experiments (especially low gravity) show that metastable surfaces can be surprisingly persistent, and that the most stable configuration can become metastable through mechanical jarring without too much difficulty. On the other hand, a metastable surface can sometimes spontaneously achieve lower energy without any input (seemingly at least) given enough time.
Boundary conditions
Boundary conditions for stress balance describe the capillary surface at the contact line: the line where a solid meets the capillary interface; also, volume constraints can serve as boundary conditions (a suspended drop, for example, has no contact line but clearly must admit a unique solution).For static surfaces, the most common contact line boundary condition is the implementation of the contact angle
Contact angle
The contact angle is the angle at which a liquid/vapor interface meets a solid surface. The contact angle is specific for any given system and is determined by the interactions across the three interfaces. Most often the concept is illustrated with a small liquid droplet resting on a flat...
, which specifies the angle that one of the fluids meets the solid wall. The contact angle condition on the surface
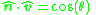
is normally written as:where
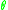is the contact angle. This condition is imposed on the boundary (or boundaries) of the surface. 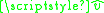is the unit outward normal to the solid surface, and 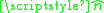is a unit normal to 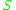. Choice of 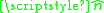depends on which fluid the contact angle is specified for.For dynamic interfaces, the boundary condition showed above works well if the contact line velocity is low. If the velocity is high, the contact angle will change ("dynamic contact angle"), and as of 2007 the mechanics of the moving contact line (or even the validity of the contact angle as a parameter) is not known and an area of active research.