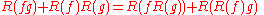Butcher group
Encyclopedia
In mathematics
, the Butcher group, named after the New Zealand mathematician John C. Butcher
by , is an infinite-dimensional group
first introduced in numerical analysis
to study solutions of non-linear ordinary differential equation
s by the Runge–Kutta method. It arose from an algebraic formalism involving rooted trees that provides formal power series
solutions of the differential equation modeling the flow of a vector field
. It was , prompted by the work of Sylvester
on change of variables in differential calculus
, who first noted that the derivatives of a composition of functions
can be conveniently expressed in terms of rooted trees and their combinatorics.
pointed out that the Butcher group is the group of characters of the Hopf algebra
of rooted trees that had arisen independently in their own work on renormalization
in quantum field theory
and Connes
' work with Moscovici on local index theorems. This Hopf algebra, often called the Connes-Kreimer algebra, is essentially equivalent to the Butcher group, since its dual can be identified with the universal enveloping algebra
of the Lie algebra
of the Butcher group. As they commented:
with a distinguished node, called the root, in which every other node is connected to the root by a unique path. If the root of a tree t is removed and the nodes connected to the original node by a single bond are taken as new roots, the tree t breaks up into rooted trees t1, t2, ... Reversing this process a new tree t = [t1, t2, ...] can be constructed by joining the roots of the trees to a new common root. The number of nodes in a tree is denoted by |t|. A heap-ordering of a rooted tree t is an allocation of the numbers 1 through |t| to the nodes so that the numbers increase on any path going away from the root. Two heap orderings are equivalent, if there is an automorphism
of rooted trees mapping one of them on the other. The number of equivalence classes of heap-orderings on a particular tree is denoted by α(t) and can be computed using the Butcher's formula:
where St denotes the symmetry group
of t and the tree factorial is defined recursively by
with the tree factorial of an isolated root defined to be 1
The ordinary differential equation for the flow of a vector field
on an open subset U of RN can be written
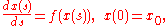
where x(s) takes values in U, f is a smooth function from U to RN and x0 is the starting point of the flow at time s = 0.
gave a method to compute the higher order derivatives x(m)(s) in terms of rooted trees. His formula can be conveniently expressed using the elementary differentials introduced by Butcher. These are defined inductively by
With this notation
giving the power series expansion
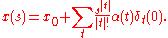
As an example when N = 1, so that x and f are real-valued functions of a single real variable, the formula yields
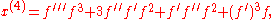
where the four terms correspond to the four rooted trees from left to right in Figure 3 above.
In a single variable this formula is the same as Faà di Bruno's formula
of 1855; however in several variables it has to be written more carefully in the form
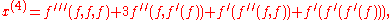
where the tree structure is crucial.
H of rooted trees was defined by in connection with Kreimer
's previous work on renormalization
in quantum field theory
. It was later discovered that the Hopf algebra was the dual of a Hopf algebra defined earlier by in a different context. The characters of H, i.e. the homomorphisms of the underlying commutative algebra into R, form a group, called the Butcher group. It corresponds to the formal group
structure discovered in numerical analysis
by .
The Hopf algebra of rooted trees H is defined to be the polynomial ring
in the variables t, where t runs through rooted trees.
where the sum is over all proper rooted subtrees s of t;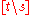
is the monomial given by the product the variables ti formed by the rooted trees that arise on erasing all the nodes of s and connected links from t. The number of such trees is denoted by n(t\s).
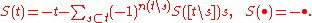
The Butcher group is defined to be the set of algebra homomorphims φ of H into R with group structure
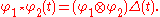
The inverse in the Butcher group is given by
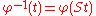
and the identity by the counit ε.
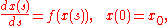
can be solved approximately by the Runge-Kutta method. This iterative scheme requires an m x m matrix
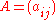
and a vector
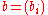
with m components.
The scheme defines vectors xn by first finding a solution X1, ... , Xm of
and then setting
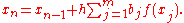
showed that the solution of the corresponding ordinary differential equations
has the power series expansion
where φj and φ are determined recursively by
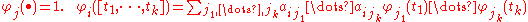
and
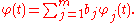
The power series above are called B-series or Butcher series. The corresponding assignment φ is an element of the Butcher group. The homomorphism corresponding to the actual flow has
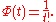
Butcher showed that the Runge-Kutta method gives an nth order approximation of the actual flow provided that φ and Φ agree on all trees with n nodes or less. Moreover showed that the homomorphisms defined by the Runge-Kutta method form a dense subgroup of the Butcher group: in fact he showed that, given a homomorphism φ', there is a Runge-Kutta homomorphism φ agreeing with φ' to order n; and that if given homomorphims φ and φ' corresponding to Runge-Kutta data (A, b) and (A' , b' ), the product homomorphism
corresponds to the data
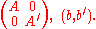
proved that the Butcher group acts naturally on the functions f. Indeed setting
they proved that
of a Lie algebra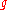
. Connes and Kreimer explicitly identify 
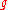with a space of derivation
s θ of H into R, i.e. linear maps such that
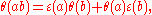
the formal tangent space of G at the identity ε. This forms a Lie algebra with Lie bracket
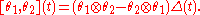
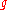is generated by the derivations θt defined by
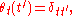
for each rooted tree t.
ic methods to give a simple mathematical formulation of renormalization
in quantum field theory
. Renormalization was interpreted as Birkhoff factorization of loops in the character group of the associated Hopf algebra. The models considered by had Hopf algebra H and character group G, the Butcher group. has given an account of this renormalization process in terms of Runge-Kutta data.
In this simplified setting, a renormalizable model has two pieces of input data:
Note that R satisfies the Rota-Baxter identity if and only if id – R does. An important example is the minimal subtraction scheme
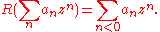
In addition there is a projection P of H onto the augmentation ideal
ker ε given by
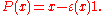
To define the renormalized Feynman rules, note that the antipode S satisfies
so that
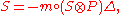
The renormalized Feynman rules are given by a homomorphism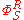
of H into V obtained by twisting the homomorphism Φ • S. The homomorphism 
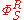is uniquely specified by
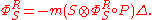
Because of the precise form of Δ, this gives a recursive formula for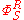
.
For the minimal subtraction scheme, this process can be interpreted in terms of Birkhoff factorization in the complex Butcher group. Φ can be regarded as a map γ of the unit circle into the complexification GC of G (maps into C instead of R). As such it has a Birkhoff factorization
where γ+ is holomorphic on the interior of the closed unit disk and γ– is holomorphic on its complement in the Riemann sphere
C
with γ–(∞) = 1. The loop γ+ corresponds to the renormalized homomorphism. The evaluation at z = 0 of γ+ or the renormalized homomorphism gives the dimensionally regularized values for each rooted tree.
In example, the Feynman rules depend on additional parameter μ, a "unit of mass". showed that
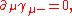
so that γμ– is independent of μ.
The complex Butcher group comes with a natural one-parameter group λw of automorphisms, dual to that on H
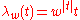
for w ≠ 0 in C.
The loops γμ and λw · γμ have the same negative part and, for t real,
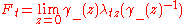
defines a one-parameter subgroup of the complex Butcher group GC called the renormalization group flow
(RG).
Its infinitesimal generator β is an element of the Lie algebra of GC and is defined by
It is called the beta-function
of the model.
In any given model, there is usually a finite-dimensional space of complex coupling constants. The complex Butcher group acts by diffeomorphims on this space. In particular the renormalization group defines a flow on the space of coupling constants, with the beta function giving the corresponding vector field.
More general models in quantum field theory require rooted trees to be replaced by Feynman diagram
s with vertices decorated by symbols from a finite index set. Connes and Kreimer have also defined Hopf algebras in this setting and have shown how they can be used to systematize standard computations in renormalization theory.
for H and the algebra V. If c is a positive integer and qμ = q / μ is a dimensionless constant, Feynman rules can be defined recursively by
where z = 1 – D/2 is the regularization parameter. These integrals can be computed explicitly in terms of the Gamma function
using the formula
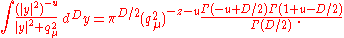
In particular
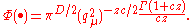
Taking the renormalization scheme R of minimal subtraction, the renormalized quantities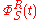
are polynomial
s in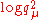
when evaluated at z = 0.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Butcher group, named after the New Zealand mathematician John C. Butcher
John C. Butcher
John Charles Butcher is a mathematician who specialises in numerical methods for the solution of ordinary differential equations. Butcher works on multistage methods for initial value problems, such as Runge-Kutta and general linear methods...
by , is an infinite-dimensional group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
first introduced in numerical analysis
Numerical analysis
Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
to study solutions of non-linear ordinary differential equation
Ordinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
s by the Runge–Kutta method. It arose from an algebraic formalism involving rooted trees that provides formal power series
Formal power series
In mathematics, formal power series are a generalization of polynomials as formal objects, where the number of terms is allowed to be infinite; this implies giving up the possibility to substitute arbitrary values for indeterminates...
solutions of the differential equation modeling the flow of a vector field
Vector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
. It was , prompted by the work of Sylvester
James Joseph Sylvester
James Joseph Sylvester was an English mathematician. He made fundamental contributions to matrix theory, invariant theory, number theory, partition theory and combinatorics...
on change of variables in differential calculus
Differential calculus
In mathematics, differential calculus is a subfield of calculus concerned with the study of the rates at which quantities change. It is one of the two traditional divisions of calculus, the other being integral calculus....
, who first noted that the derivatives of a composition of functions
Faà di Bruno's formula
Faà di Bruno's formula is an identity in mathematics generalizing the chain rule to higher derivatives, named after , though he was not the first to state or prove the formula...
can be conveniently expressed in terms of rooted trees and their combinatorics.
pointed out that the Butcher group is the group of characters of the Hopf algebra
Hopf algebra
In mathematics, a Hopf algebra, named after Heinz Hopf, is a structure that is simultaneously an algebra and a coalgebra, with these structures' compatibility making it a bialgebra, and that moreover is equipped with an antiautomorphism satisfying a certain property.Hopf algebras occur naturally...
of rooted trees that had arisen independently in their own work on renormalization
Renormalization
In quantum field theory, the statistical mechanics of fields, and the theory of self-similar geometric structures, renormalization is any of a collection of techniques used to treat infinities arising in calculated quantities....
in quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
and Connes
Alain Connes
Alain Connes is a French mathematician, currently Professor at the Collège de France, IHÉS, The Ohio State University and Vanderbilt University.-Work:...
' work with Moscovici on local index theorems. This Hopf algebra, often called the Connes-Kreimer algebra, is essentially equivalent to the Butcher group, since its dual can be identified with the universal enveloping algebra
Universal enveloping algebra
In mathematics, for any Lie algebra L one can construct its universal enveloping algebra U. This construction passes from the non-associative structure L to a unital associative algebra which captures the important properties of L.Any associative algebra A over the field K becomes a Lie algebra...
of the Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
of the Butcher group. As they commented:
Differentials and rooted trees
A rooted tree is a graphGraph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
with a distinguished node, called the root, in which every other node is connected to the root by a unique path. If the root of a tree t is removed and the nodes connected to the original node by a single bond are taken as new roots, the tree t breaks up into rooted trees t1, t2, ... Reversing this process a new tree t = [t1, t2, ...] can be constructed by joining the roots of the trees to a new common root. The number of nodes in a tree is denoted by |t|. A heap-ordering of a rooted tree t is an allocation of the numbers 1 through |t| to the nodes so that the numbers increase on any path going away from the root. Two heap orderings are equivalent, if there is an automorphism
Automorphism
In mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism...
of rooted trees mapping one of them on the other. The number of equivalence classes of heap-orderings on a particular tree is denoted by α(t) and can be computed using the Butcher's formula:
where St denotes the symmetry group
Symmetry group
The symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation...
of t and the tree factorial is defined recursively by
with the tree factorial of an isolated root defined to be 1
The ordinary differential equation for the flow of a vector field
Vector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
on an open subset U of RN can be written
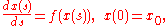
where x(s) takes values in U, f is a smooth function from U to RN and x0 is the starting point of the flow at time s = 0.
gave a method to compute the higher order derivatives x(m)(s) in terms of rooted trees. His formula can be conveniently expressed using the elementary differentials introduced by Butcher. These are defined inductively by
With this notation
giving the power series expansion
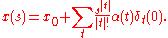
As an example when N = 1, so that x and f are real-valued functions of a single real variable, the formula yields
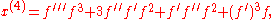
where the four terms correspond to the four rooted trees from left to right in Figure 3 above.
In a single variable this formula is the same as Faà di Bruno's formula
Faà di Bruno's formula
Faà di Bruno's formula is an identity in mathematics generalizing the chain rule to higher derivatives, named after , though he was not the first to state or prove the formula...
of 1855; however in several variables it has to be written more carefully in the form
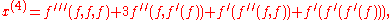
where the tree structure is crucial.
Definition using Hopf algebra of rooted trees
The Hopf algebraHopf algebra
In mathematics, a Hopf algebra, named after Heinz Hopf, is a structure that is simultaneously an algebra and a coalgebra, with these structures' compatibility making it a bialgebra, and that moreover is equipped with an antiautomorphism satisfying a certain property.Hopf algebras occur naturally...
H of rooted trees was defined by in connection with Kreimer
Dirk Kreimer
Dirk Kreimer is a German physicist who pioneered the Hopf-algebraic approach to quantum field theory with Alain Connes and other co-authors. He is currently affiliated with IHES and Boston University.-External links:*...
's previous work on renormalization
Renormalization
In quantum field theory, the statistical mechanics of fields, and the theory of self-similar geometric structures, renormalization is any of a collection of techniques used to treat infinities arising in calculated quantities....
in quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
. It was later discovered that the Hopf algebra was the dual of a Hopf algebra defined earlier by in a different context. The characters of H, i.e. the homomorphisms of the underlying commutative algebra into R, form a group, called the Butcher group. It corresponds to the formal group
Formal group
In mathematics, a formal group law is a formal power series behaving as if it were the product of a Lie group. They were introduced by . The term formal group sometimes means the same as formal group law, and sometimes means one of several generalizations. Formal groups are intermediate between...
structure discovered in numerical analysis
Numerical analysis
Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
by .
The Hopf algebra of rooted trees H is defined to be the polynomial ring
Polynomial ring
In mathematics, especially in the field of abstract algebra, a polynomial ring is a ring formed from the set of polynomials in one or more variables with coefficients in another ring. Polynomial rings have influenced much of mathematics, from the Hilbert basis theorem, to the construction of...
in the variables t, where t runs through rooted trees.
- Its comultiplication
is defined by
where the sum is over all proper rooted subtrees s of t;
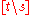is the monomial given by the product the variables ti formed by the rooted trees that arise on erasing all the nodes of s and connected links from t. The number of such trees is denoted by n(t\s).- Its counit is the homomorphism ε of H into R sending each variable t to zero.
- Its antipodeAntipodeAntipode, Antipodes, or Antipodeans may refer to:* Antipodal point, the diametrically opposite point on a sphere* Antipodes Water Company, a premium bottled water brand...
S can be defined recursively by the formula
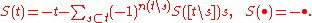
The Butcher group is defined to be the set of algebra homomorphims φ of H into R with group structure
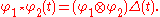
The inverse in the Butcher group is given by
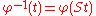
and the identity by the counit ε.
Butcher series and Runge–Kutta method
The non-linear ordinary differential equation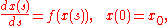can be solved approximately by the Runge-Kutta method. This iterative scheme requires an m x m matrix
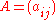
and a vector
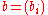
with m components.
The scheme defines vectors xn by first finding a solution X1, ... , Xm of
and then setting
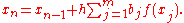
showed that the solution of the corresponding ordinary differential equations
has the power series expansion
where φj and φ are determined recursively by
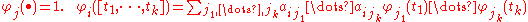
and
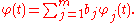
The power series above are called B-series or Butcher series. The corresponding assignment φ is an element of the Butcher group. The homomorphism corresponding to the actual flow has
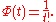
Butcher showed that the Runge-Kutta method gives an nth order approximation of the actual flow provided that φ and Φ agree on all trees with n nodes or less. Moreover showed that the homomorphisms defined by the Runge-Kutta method form a dense subgroup of the Butcher group: in fact he showed that, given a homomorphism φ', there is a Runge-Kutta homomorphism φ agreeing with φ' to order n; and that if given homomorphims φ and φ' corresponding to Runge-Kutta data (A, b) and (A' , b' ), the product homomorphism
corresponds to the data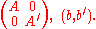proved that the Butcher group acts naturally on the functions f. Indeed setting
they proved that
Lie algebra
showed that associated with the Butcher group G is an infinite-dimensional Lie algebra. The existence of this Lie algebra is predicted by a theorem of : the commutativity and natural grading on H implies that the dual H* can be identified with the universal enveloping algebraUniversal enveloping algebra
In mathematics, for any Lie algebra L one can construct its universal enveloping algebra U. This construction passes from the non-associative structure L to a unital associative algebra which captures the important properties of L.Any associative algebra A over the field K becomes a Lie algebra...
of a Lie algebra
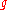. Connes and Kreimer explicitly identify 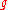with a space of derivationDerivation
Derivation may refer to:* Derivation , a function on an algebra which generalizes certain features of the derivative operator* Derivation * Derivation in differential algebra, a unary function satisfying the Leibniz product law...
s θ of H into R, i.e. linear maps such that
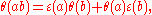
the formal tangent space of G at the identity ε. This forms a Lie algebra with Lie bracket
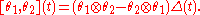
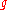is generated by the derivations θt defined by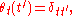for each rooted tree t.
Renormalization
provided a general context for using Hopf algebraHopf algebra
In mathematics, a Hopf algebra, named after Heinz Hopf, is a structure that is simultaneously an algebra and a coalgebra, with these structures' compatibility making it a bialgebra, and that moreover is equipped with an antiautomorphism satisfying a certain property.Hopf algebras occur naturally...
ic methods to give a simple mathematical formulation of renormalization
Renormalization
In quantum field theory, the statistical mechanics of fields, and the theory of self-similar geometric structures, renormalization is any of a collection of techniques used to treat infinities arising in calculated quantities....
in quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
. Renormalization was interpreted as Birkhoff factorization of loops in the character group of the associated Hopf algebra. The models considered by had Hopf algebra H and character group G, the Butcher group. has given an account of this renormalization process in terms of Runge-Kutta data.
In this simplified setting, a renormalizable model has two pieces of input data:
- a set of Feynman rules given by an algebra homomorphism Φ of H into the algebra V of Laurent seriesLaurent seriesIn mathematics, the Laurent series of a complex function f is a representation of that function as a power series which includes terms of negative degree. It may be used to express complex functions in cases where...
in z with poles of finite order; - a renormalization scheme given by a linear operator R on V such that R satisfies the Rota-Baxter identity
-
- and the image of R – id lies in the algebra V+ of power series in z.
Note that R satisfies the Rota-Baxter identity if and only if id – R does. An important example is the minimal subtraction scheme
Minimal subtraction scheme
In quantum field theory, the minimal subtraction scheme, or MS scheme is a particular renormalization scheme used to absorb the infinities that arise in perturbative calculations beyond leading order, introduced independently by and...
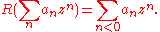
In addition there is a projection P of H onto the augmentation ideal
Augmentation ideal
In algebra, an augmentation ideal is an ideal that can be defined in any group ring. If G is a group and R a commutative ring, there is a ring homomorphism \varepsilon, called the augmentation map, from the group ring...
ker ε given by
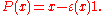
To define the renormalized Feynman rules, note that the antipode S satisfies
so that
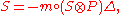
The renormalized Feynman rules are given by a homomorphism
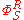of H into V obtained by twisting the homomorphism Φ • S. The homomorphism 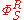is uniquely specified by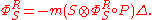Because of the precise form of Δ, this gives a recursive formula for
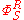.For the minimal subtraction scheme, this process can be interpreted in terms of Birkhoff factorization in the complex Butcher group. Φ can be regarded as a map γ of the unit circle into the complexification GC of G (maps into C instead of R). As such it has a Birkhoff factorization
where γ+ is holomorphic on the interior of the closed unit disk and γ– is holomorphic on its complement in the Riemann sphere
Riemann sphere
In mathematics, the Riemann sphere , named after the 19th century mathematician Bernhard Riemann, is the sphere obtained from the complex plane by adding a point at infinity...
C
with γ–(∞) = 1. The loop γ+ corresponds to the renormalized homomorphism. The evaluation at z = 0 of γ+ or the renormalized homomorphism gives the dimensionally regularized values for each rooted tree.In example, the Feynman rules depend on additional parameter μ, a "unit of mass". showed that
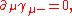
so that γμ– is independent of μ.
The complex Butcher group comes with a natural one-parameter group λw of automorphisms, dual to that on H
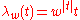
for w ≠ 0 in C.
The loops γμ and λw · γμ have the same negative part and, for t real,
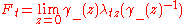
defines a one-parameter subgroup of the complex Butcher group GC called the renormalization group flow
Renormalization group
In theoretical physics, the renormalization group refers to a mathematical apparatus that allows systematic investigation of the changes of a physical system as viewed at different distance scales...
(RG).
Its infinitesimal generator β is an element of the Lie algebra of GC and is defined by
It is called the beta-function
Beta-function
In theoretical physics, specifically quantum field theory, a beta function β encodes the dependence of a coupling parameter, g, on the energy scale, \mu of a given physical process....
of the model.
In any given model, there is usually a finite-dimensional space of complex coupling constants. The complex Butcher group acts by diffeomorphims on this space. In particular the renormalization group defines a flow on the space of coupling constants, with the beta function giving the corresponding vector field.
More general models in quantum field theory require rooted trees to be replaced by Feynman diagram
Feynman diagram
Feynman diagrams are a pictorial representation scheme for the mathematical expressions governing the behavior of subatomic particles, first developed by the Nobel Prize-winning American physicist Richard Feynman, and first introduced in 1948...
s with vertices decorated by symbols from a finite index set. Connes and Kreimer have also defined Hopf algebras in this setting and have shown how they can be used to systematize standard computations in renormalization theory.
Example
has given a "toy model" involving dimensional regularizationDimensional regularization
In theoretical physics, dimensional regularization is a method introduced by Giambiagi and Bollini for regularizing integrals in the evaluation of Feynman diagrams; in other words, assigning values to them that are meromorphic functions of an auxiliary complex parameter d, called the...
for H and the algebra V. If c is a positive integer and qμ = q / μ is a dimensionless constant, Feynman rules can be defined recursively by
where z = 1 – D/2 is the regularization parameter. These integrals can be computed explicitly in terms of the Gamma function
Gamma function
In mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...
using the formula
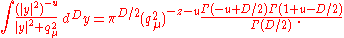
In particular
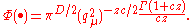
Taking the renormalization scheme R of minimal subtraction, the renormalized quantities
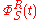are polynomialPolynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
s in
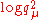when evaluated at z = 0.