Bracket (mathematics)
Encyclopedia
In mathematics
, various typographical forms of bracket
s are frequently used in mathematical notation
such as parentheses ( ), square brackets [ ], curly brackets { }, and angle brackets
. In the typical use, a mathematical expression is enclosed between an "opening bracket" and a matching "closing bracket". Generally such bracketing denotes some form of grouping: in evaluating an expression containing a bracketed sub-expression, the operators in the sub-expression take precedence over those surrounding it. Additionally, there are several specific uses and meanings for the various brackets.
Historically, other notations, such as the vinculum, were similarly used for grouping; in present-day use, these notations have all specific meanings. The earliest use of brackets to indicate aggregation (i.e. grouping) was suggested in 1608 by Christoforus Clavius and in 1629 by Albert Girard
.
In the Z
formal specification
language, curly braces denote a set and angle brackets denote a sequence.
text it is common to use the less-than (<) and greater-than (>) signs to represent angle brackets. Unicode
has three pairs of dedicated characters:
In LaTeX
the markup is \langle and \rangle: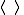
.
parentheses, , are used to specify the order of operations
, terms inside the bracket are evaluated first, hence 2×(3 + 4) is 14 and (2×3) + 4 is 10. This notation is extended to cover more general algebra
involving variables: for example
. Square brackets are also often used in place of a second set of parentheses when they are nested, to provide a visual distinction.
Also in mathematical expressions in general, parentheses are used to indicate grouping (that is, which parts belong together) when necessary to avoid ambiguities, or for the sake of clarity. For example, in the formula (εη)X = εXηX, used in the definition of composition of two natural transformation
s, the parentheses around εη serve to indicate that the indexing by X is applied to the composition εη, and not just its last component η.
are frequently surrounded by brackets: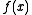
. It is common to omit the parentheses around the argument when there is little chance of ambiguity, thus: 
.
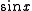brackets are used to specify the coordinates of a point: (2,3) denotes the point with x-coordinate 2 and y-coordinate 3.
The inner product of two vectors is commonly written as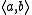
, but the notation (a, b) is also used.
. The notation[a, c) is used to indicate an interval from a to c that is inclusive of a but exclusive of c. That is, [5, 12) would be the set of all real numbers between 5 and 12, including 5 but not 12. The numbers may come as close as they like to 12, including 11.999 and so forth (with any finite number of 9s), but 12.0 is not included. In Europe, the notation [5,12[ is also used for this.
The endpoint adjoining the square bracket is known as closed, while the endpoint adjoining the parenthesis is known as open. If both types of brackets are the same, the entire interval may be referred to as closed or open as appropriate. Whenever infinity
or negative infinity is used as an endpoint in the case of intervals on the real number line, it is always considered open and adjoined to a parenthesis. The endpoint can be closed when considering intervals on the extended real number line
.
Angle brackets are used in group theory
to write group presentations, and to denote the subgroup generated by a collection of elements.
is commonly written between large round or square brackets:
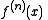
stands for the n-th derivative of function f, applied to argument x. So, for example, if f(x) = exp(λx), f(n)(x) = λnexp(λx). This is to be contrasted with fn(x) = f(f(...(f(x))...)), the n-fold application of f to argument x.
defined by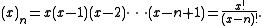
Confusingly, the same notation may be encountered as representing the rising factorial, also called "Pochhammer symbol
". Another notation for the same is x(n). It can be defined by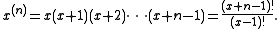
, angle brackets are also used as part of Dirac
's formalism, bra-ket notation
, to note vectors from the dual space
s of the bra
and the ket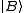 
.
In statistical mechanics, angle brackets denote ensemble or time average.
and ring theory
, square brackets are used to denote the commutator
. In group theory, the commutator[ g,h] is commonly defined as g−1h−1gh. In ring theory, the commutator [ a,b] is defined as ab − ba. Furthermore, in ring theory, braces are used to denote the anticommutator
where {a,b} is defined as ab + ba.
The Lie bracket of a Lie algebra
is a binary operation
denoted by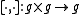
. By using the commutator as a Lie bracket, every associative algebra can be turned into a Lie algebra. There are many different forms of Lie bracket, in particular the Lie derivative
and the Jacobi-Lie bracket.
, which rounds
a real number down to the next integer.
However the floor and ceiling functions are usually typeset with left and right square brackets where the upper (for floor function) or lower (for ceiling function) horizontal bars are missing, as in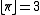
or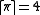 
.
Curly brackets, as in , may denote the fractional part
of a real number.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, various typographical forms of bracket
Bracket
Brackets are tall punctuation marks used in matched pairs within text, to set apart or interject other text. In the United States, "bracket" usually refers specifically to the "square" or "box" type.-List of types:...
s are frequently used in mathematical notation
Mathematical notation
Mathematical notation is a system of symbolic representations of mathematical objects and ideas. Mathematical notations are used in mathematics, the physical sciences, engineering, and economics...
such as parentheses ( ), square brackets [ ], curly brackets { }, and angle brackets
. In the typical use, a mathematical expression is enclosed between an "opening bracket" and a matching "closing bracket". Generally such bracketing denotes some form of grouping: in evaluating an expression containing a bracketed sub-expression, the operators in the sub-expression take precedence over those surrounding it. Additionally, there are several specific uses and meanings for the various brackets.Historically, other notations, such as the vinculum, were similarly used for grouping; in present-day use, these notations have all specific meanings. The earliest use of brackets to indicate aggregation (i.e. grouping) was suggested in 1608 by Christoforus Clavius and in 1629 by Albert Girard
Albert Girard
Albert Girard was a French-born mathematician. He studied at the University of Leiden. He "had early thoughts on the fundamental theorem of algebra" and gave the inductive definition for the Fibonacci numbers....
.
In the Z
Z notation
The Z notation , named after Zermelo–Fraenkel set theory, is a formal specification language used for describing and modelling computing systems. It is targeted at the clear specification of computer programs and computer-based systems in general.-History:...
formal specification
Formal specification
In computer science, a formal specification is a mathematical description of software or hardware that may be used to develop an implementation. It describes what the system should do, not how the system should do it...
language, curly braces denote a set and angle brackets denote a sequence.
Symbols for representing angle brackets
A variety of different symbols are used to represent angle brackets. In e-mail and other ASCIIASCII
The American Standard Code for Information Interchange is a character-encoding scheme based on the ordering of the English alphabet. ASCII codes represent text in computers, communications equipment, and other devices that use text...
text it is common to use the less-than (<) and greater-than (>) signs to represent angle brackets. Unicode
Unicode
Unicode is a computing industry standard for the consistent encoding, representation and handling of text expressed in most of the world's writing systems...
has three pairs of dedicated characters:
- U+2329 (〈) and U+232A (〉) (left/right-pointing angle bracket) which are deprecated
- U+27E8 (⟨) and U+27E9 (⟩) (mathematical left/right angle bracket)
- U+3008 (〈) and U+3009 (〉) (left/right angle bracket in Chinese punctuation)
In LaTeX
LaTeX
LaTeX is a document markup language and document preparation system for the TeX typesetting program. Within the typesetting system, its name is styled as . The term LaTeX refers only to the language in which documents are written, not to the editor used to write those documents. In order to...
the markup is \langle and \rangle:
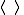.Algebra
In elementary algebraElementary algebra
Elementary algebra is a fundamental and relatively basic form of algebra taught to students who are presumed to have little or no formal knowledge of mathematics beyond arithmetic. It is typically taught in secondary school under the term algebra. The major difference between algebra and...
parentheses, , are used to specify the order of operations
Order of operations
In mathematics and computer programming, the order of operations is a rule used to clarify unambiguously which procedures should be performed first in a given mathematical expression....
, terms inside the bracket are evaluated first, hence 2×(3 + 4) is 14 and (2×3) + 4 is 10. This notation is extended to cover more general algebra
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
involving variables: for example
. Square brackets are also often used in place of a second set of parentheses when they are nested, to provide a visual distinction.Also in mathematical expressions in general, parentheses are used to indicate grouping (that is, which parts belong together) when necessary to avoid ambiguities, or for the sake of clarity. For example, in the formula (εη)X = εXηX, used in the definition of composition of two natural transformation
Natural transformation
In category theory, a branch of mathematics, a natural transformation provides a way of transforming one functor into another while respecting the internal structure of the categories involved. Hence, a natural transformation can be considered to be a "morphism of functors". Indeed this intuition...
s, the parentheses around εη serve to indicate that the indexing by X is applied to the composition εη, and not just its last component η.
Functions
The arguments to a functionFunction (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
are frequently surrounded by brackets:
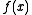. It is common to omit the parentheses around the argument when there is little chance of ambiguity, thus: 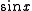.Coordinates and vectors
In the cartesian coordinate systemCartesian coordinate system
A Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
brackets are used to specify the coordinates of a point: (2,3) denotes the point with x-coordinate 2 and y-coordinate 3.
The inner product of two vectors is commonly written as
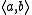, but the notation (a, b) is also used.Intervals
Both parentheses, , and square brackets, [ ], can also be used to denote an intervalInterval (mathematics)
In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
. The notation
The endpoint adjoining the square bracket is known as closed, while the endpoint adjoining the parenthesis is known as open. If both types of brackets are the same, the entire interval may be referred to as closed or open as appropriate. Whenever infinity
Infinity
Infinity is a concept in many fields, most predominantly mathematics and physics, that refers to a quantity without bound or end. People have developed various ideas throughout history about the nature of infinity...
or negative infinity is used as an endpoint in the case of intervals on the real number line, it is always considered open and adjoined to a parenthesis. The endpoint can be closed when considering intervals on the extended real number line
Extended real number line
In mathematics, the affinely extended real number system is obtained from the real number system R by adding two elements: +∞ and −∞ . The projective extended real number system adds a single object, ∞ and makes no distinction between "positive" or "negative" infinity...
.
Sets and groups
Curly brackets { } are used to identify the elements of a set: {a,b,c} denotes a set of three elements.Angle brackets are used in group theory
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
to write group presentations, and to denote the subgroup generated by a collection of elements.
Matrices
An explicitly given matrixMatrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
is commonly written between large round or square brackets:
Derivatives
The notation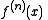stands for the n-th derivative of function f, applied to argument x. So, for example, if f(x) = exp(λx), f(n)(x) = λnexp(λx). This is to be contrasted with fn(x) = f(f(...(f(x))...)), the n-fold application of f to argument x.
Falling and rising factorial
The notation (x)n is used to denote the falling factorial, an n-th degree polynomialPolynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
defined by
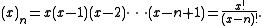
Confusingly, the same notation may be encountered as representing the rising factorial, also called "Pochhammer symbol
Pochhammer symbol
In mathematics, the Pochhammer symbol introduced by Leo August Pochhammer is the notation ', where is a non-negative integer. Depending on the context the Pochhammer symbol may represent either the rising factorial or the falling factorial as defined below. Care needs to be taken to check which...
". Another notation for the same is x(n). It can be defined by
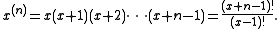
Quantum mechanics
In quantum mechanicsQuantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
, angle brackets are also used as part of Dirac
Paul Dirac
Paul Adrien Maurice Dirac, OM, FRS was an English theoretical physicist who made fundamental contributions to the early development of both quantum mechanics and quantum electrodynamics...
's formalism, bra-ket notation
Bra-ket notation
Bra-ket notation is a standard notation for describing quantum states in the theory of quantum mechanics composed of angle brackets and vertical bars. It can also be used to denote abstract vectors and linear functionals in mathematics...
, to note vectors from the dual space
Dual space
In mathematics, any vector space, V, has a corresponding dual vector space consisting of all linear functionals on V. Dual vector spaces defined on finite-dimensional vector spaces can be used for defining tensors which are studied in tensor algebra...
s of the bra
and the ket 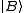.In statistical mechanics, angle brackets denote ensemble or time average.
Lie bracket and commutator
In group theoryGroup theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
and ring theory
Ring theory
In abstract algebra, ring theory is the study of rings—algebraic structures in which addition and multiplication are defined and have similar properties to those familiar from the integers...
, square brackets are used to denote the commutator
Commutator
In mathematics, the commutator gives an indication of the extent to which a certain binary operation fails to be commutative. There are different definitions used in group theory and ring theory.-Group theory:...
. In group theory, the commutator
Commutator
In mathematics, the commutator gives an indication of the extent to which a certain binary operation fails to be commutative. There are different definitions used in group theory and ring theory.-Group theory:...
where {a,b} is defined as ab + ba.
The Lie bracket of a Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
is a binary operation
Binary operation
In mathematics, a binary operation is a calculation involving two operands, in other words, an operation whose arity is two. Examples include the familiar arithmetic operations of addition, subtraction, multiplication and division....
denoted by
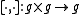. By using the commutator as a Lie bracket, every associative algebra can be turned into a Lie algebra. There are many different forms of Lie bracket, in particular the Lie derivativeLie derivative
In mathematics, the Lie derivative , named after Sophus Lie by Władysław Ślebodziński, evaluates the change of a vector field or more generally a tensor field, along the flow of another vector field...
and the Jacobi-Lie bracket.
Floor / Ceiling functions and fractional part
Square brackets, as in , are sometimes used to denote the floor functionFloor function
In mathematics and computer science, the floor and ceiling functions map a real number to the largest previous or the smallest following integer, respectively...
, which rounds
Rounding
Rounding a numerical value means replacing it by another value that is approximately equal but has a shorter, simpler, or more explicit representation; for example, replacing $23.4476 with $23.45, or the fraction 312/937 with 1/3, or the expression √2 with 1.414.Rounding is often done on purpose to...
a real number down to the next integer.
However the floor and ceiling functions are usually typeset with left and right square brackets where the upper (for floor function) or lower (for ceiling function) horizontal bars are missing, as in
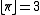or 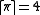.Curly brackets, as in , may denote the fractional part
Fractional part
All real numbers can be written in the form n + r where n is an integer and the remaining fractional part r is a nonnegative real number less than one...
of a real number.
Highest common factor
The notation (a, b) is sometimes used to denote the highest common factor of a and b. This may be extended to three or more arguments.See also
- Iverson bracket
- Algebraic bracketAlgebraic bracketIn mathematics, the algebraic bracket or Nijenhuis–Richardson bracket is a graded Lie algebra structure on the space of alternating multilinear forms of a vector space to itself, introduced by A. Nijenhuis and R. W. Richardson, Jr...
- Binomial coefficientBinomial coefficientIn mathematics, binomial coefficients are a family of positive integers that occur as coefficients in the binomial theorem. They are indexed by two nonnegative integers; the binomial coefficient indexed by n and k is usually written \tbinom nk , and it is the coefficient of the x k term in...
- Poisson bracketPoisson bracketIn mathematics and classical mechanics, the Poisson bracket is an important binary operation in Hamiltonian mechanics, playing a central role in Hamilton's equations of motion, which govern the time-evolution of a Hamiltonian dynamical system...
- Bracket polynomialBracket polynomialIn the mathematical field of knot theory, the bracket polynomial is a polynomial invariant of framed links. Although it is not an invariant of knots or links , a suitably "normalized" version yields the famous knot invariant called the Jones polynomial...
- Pochhammer symbolPochhammer symbolIn mathematics, the Pochhammer symbol introduced by Leo August Pochhammer is the notation ', where is a non-negative integer. Depending on the context the Pochhammer symbol may represent either the rising factorial or the falling factorial as defined below. Care needs to be taken to check which...
- Frölicher-Nijenhuis bracketFrölicher-Nijenhuis bracketIn mathematics, the Frölicher–Nijenhuis bracket is an extension of the Lie bracket of vector fields to vector-valued differential forms on a differentiable manifold...
- Nijenhuis-Richardson bracket
- Schouten-Nijenhuis bracketSchouten-Nijenhuis bracketIn differential geometry, the Schouten–Nijenhuis bracket, also known as the Schouten bracket, is a type of graded Lie bracket defined on multivector fields on a smooth manifold extending the Lie bracket of vector fields. There are two different versions, both rather confusingly called by the same...
- Dyck languageDyck languageIn the theory of formal languages of computer science, mathematics, and linguistics, the Dyck language is the language consisting of balanced strings of parentheses [ and ]. It is important in the parsing of expressions that must have a correctly nested sequence of parentheses, such as arithmetic...