In differential geometry, the Schouten–Nijenhuis bracket, also known as the Schouten bracket, is a type of graded Lie bracket

Graded Lie algebra

In mathematics, a graded Lie algebra is a Lie algebra endowed with a gradation which is compatible with the Lie bracket. In other words, a graded Lie algebra is a Lie algebra which is also a nonassociative graded algebra under the bracket operation. A choice of Cartan decomposition endows any...

 defined on multivector

Multivector

In multilinear algebra, a multivector or clif is an element of the exterior algebra on a vector space, \Lambda^* V. This algebra consists of linear combinations of simple k-vectors v_1\wedge\cdots\wedge v_k."Multivector" may mean either homogeneous elements In multilinear algebra, a multivector...

 fields

Vector field

In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...

 on a smooth manifold extending the Lie bracket of vector fields

Lie bracket of vector fields

In the mathematical field of differential topology, the Lie bracket of vector fields, Jacobi–Lie bracket, or commutator of vector fields is a bilinear differential operator which assigns, to any two vector fields X and Y on a smooth manifold M, a third vector field denoted [X, Y]...

. There are two different versions, both rather confusingly called by the same name. The most common version is defined on alternating multivector fields and makes them into a Gerstenhaber algebra, but there is also another version defined on symmetric multivector fields, which is more or less the same as the Poisson bracket on the cotangent bundle. It was discovered by Jan Arnoldus Schouten

Jan Arnoldus Schouten

Jan Arnoldus Schouten was a Dutch mathematician. He was an important contributor to the development of tensor calculus and was one of the founders of the Mathematisch Centrum in Amsterdam....

 (1940, 1953) and its properties were investigated by his student Albert Nijenhuis

Albert Nijenhuis

Albert Nijenhuis is a Dutch mathematician at the University of Washington and the University of Pennsylvania working on combinatorics and differential geometry, who introduced the Nijenhuis tensor , the Schouten-Nijenhuis bracket , the Frölicher-Nijenhuis bracket , and the Nijenhuis-Richardson...

 (1955). It is related to but not the same as the Nijenhuis–Richardson bracket and the Frölicher–Nijenhuis bracket.

Definition and properties

An alternating multivector field is a section of the exterior algebra

Exterior algebra

In mathematics, the exterior product or wedge product of vectors is an algebraic construction used in Euclidean geometry to study areas, volumes, and their higher-dimensional analogs...

 ∧^∗TM over the tangent bundle

Tangent bundle

In differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...

 of a manifold M. The alternating multivector fields form a graded supercommutative ring with the product of a and b written as ab (some authors use a∧b). This is dual to the usual algebra of differential forms Ω^∗M by the pairing on homogeneous elements:

The degree of a multivector A in ∧^pTM is defined to be |A| = p.

The skew symmetric Schouten–Nijenhuis bracket is the unique extension of the Lie bracket of vector fields to a graded bracket on the space of alternating multivector fields that makes the alternating multivector fields into a Gerstenhaber algebra.
It is given in terms of the Lie bracket of vector fields by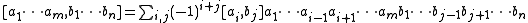
for vector fields a_i, b_j and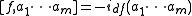
for vector fields a_i and smooth function f, where i_df is the common inner product operator.
It has the following properties.

• |ab| = |a| + |b| (The product has degree 0)
• |[a,b]| = |a| + |b| − 1 (The Schouten–Nijenhuis bracket has degree −1)
• (ab)c = a(bc), ab = (−1)^|a||b|ba (the product is associative and (super) commutative)
• [a, bc] = [a, b]c + (−1)^{|b|(|a| − 1)}b[a, c] (Poisson identity)
• [a,b] = −(−1)^{(|a| − 1)(|b| − 1)} [b,a] (Antisymmetry of Schouten–Nijenhuis bracket)
• a,b],c] = [a,[b,c − (−1)^{(|a| − 1)(|b| − 1)}[b,[a,c]] (Jacobi identity for Schouten–Nijenhuis bracket)
• If f and g are functions (multivectors homogeneous of degree 0), then [f,g] = 0.
• If a is a vector field, then [a,b] = L_ab is the usual Lie derivative
  Lie derivative
  In mathematics, the Lie derivative , named after Sophus Lie by Władysław Ślebodziński, evaluates the change of a vector field or more generally a tensor field, along the flow of another vector field...
  
   of the multivector field b along a, and in particular if a and b are vector fields then the Schouten–Nijenhuis bracket is the usual Lie bracket of vector fields
  Lie bracket of vector fields
  In the mathematical field of differential topology, the Lie bracket of vector fields, Jacobi–Lie bracket, or commutator of vector fields is a bilinear differential operator which assigns, to any two vector fields X and Y on a smooth manifold M, a third vector field denoted [X, Y]...
  
  .

The Schouten–Nijenhuis bracket makes the multivector fields into a Lie superalgebra if the grading
is changed to the one of opposite parity (so that the even and odd subspaces are switched), though
with this new grading it is no longer a supercommutative ring. Accordingly, the Jacobi identity may also be expressed in the symmetrical form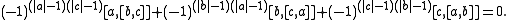

Generalizations

There is a common generalization of the Schouten–Nijenhuis bracket for alternating multivector fields and the Frölicher–Nijenhuis bracket due to Vinogradov (1990).

A version of the Schouten–Nijenhuis bracket can also be defined for symmetric multivector fields in a similar way. The symmetric multivector fields can be identified with functions on the cotangent space T^*(M) of M that are polynomial in the fiber, and under this identification the symmetric Schouten–Nijenhuis bracket corresponds to the Poisson bracket

Poisson bracket

In mathematics and classical mechanics, the Poisson bracket is an important binary operation in Hamiltonian mechanics, playing a central role in Hamilton's equations of motion, which govern the time-evolution of a Hamiltonian dynamical system...

 of functions on the symplectic manifold

Symplectic manifold

In mathematics, a symplectic manifold is a smooth manifold, M, equipped with a closed nondegenerate differential 2-form, ω, called the symplectic form. The study of symplectic manifolds is called symplectic geometry or symplectic topology...

 T^*(M).
There is a common generalization of the Schouten–Nijenhuis bracket for symmetric multivector fields and the Frölicher–Nijenhuis bracket due to Dubois-Violette and Peter W. Michor (1995).

External links

• Nicola Ciccoli Schouten–Nijenhuis bracket in notes on From Poisson to Quantum Geometry

The source of this article is wikipedia, the free encyclopedia.  The text of this article is licensed under the GFDL.