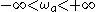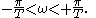Bilinear transform
Encyclopedia
The bilinear transform is used in digital signal processing
and discrete-time control theory
to transform continuous-time system representations to discrete-time and vice versa.
The bilinear transform is a special case of a conformal map
ping (namely, the Möbius transformation), often used to convert a transfer function
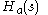of a linear
, time-invariant (LTI
) filter in the continuous
-time domain (often called an analog filter) to a transfer function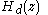
of a linear, shift-invariant filter in the discrete
-time domain (often called a digital filter
although there are analog filters constructed with switched capacitor
s that are discrete-time filters). It maps positions on the
axis, 
, in the s-plane to the unit circle
,
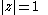, in the z-plane
. Other bilinear transforms can be used to warp the frequency response
of any discrete-time linear system (for example to approximate the non-linear frequency resolution of the human auditory system) and are implementable in the discrete domain by replacing a system's unit delays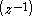
with first order all-pass filter
s.
The transform preserves stability
and maps every point of the frequency response
of the continuous-time filter,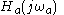
to a corresponding point in the frequency response of the discrete-time filter, 
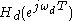although to a somewhat different frequency, as shown in the Frequency warping section below. This means that for every feature that one sees in the frequency response of the analog filter, there is a corresponding feature, with identical gain and phase shift, in the frequency response of the digital filter but, perhaps, at a somewhat different frequency. This is barely noticeable at low frequencies but is quite evident at frequencies close to the Nyquist frequency
.
), the result is precisely the Z transform of the discrete-time sequence with the substitution of
where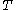
is the numerical integration
step size of the trapezoidal rule used in the bilinear transform derivation. The above bilinear approximation can be solved for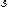
or a similar approximation for 
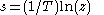can be performed.
The inverse of this mapping (and its first-order bilinear approximation) is
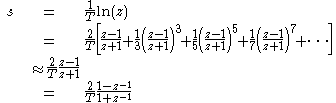
The bilinear transform essentially uses this first order approximation and substitutes into the continuous-time transfer function,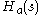
That is
if the poles of its transfer function fall in the left half of the complex
s-plane. A discrete-time causal filter is stable if the poles of its transfer function fall inside the unit circle
in the complex z-plane
. The bilinear transform maps the left half of the complex s-plane to the interior of the unit circle in the z-plane. Thus filters designed in the continuous-time domain that are stable are converted to filters in the discrete-time domain that preserve that stability.
Likewise, a continuous-time filter is minimum-phase if the zeros
of its transfer function fall in the left half of the complex s-plane. A discrete-time filter is minimum-phase if the zeros of its transfer function fall inside the unit circle in the complex z-plane. Then the same mapping property assures that continuous-time filters that are minimum-phase are converted to discrete-time filters that preserve that property of being minimum-phase.
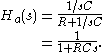
If we wish to implement this filter as a digital filter, we can apply the bilinear transform by substituting for
the formula above; after some reworking, we get the following filter representation:
The coefficients of the denominator are the 'feed-backward' coefficients and the coefficients of the numerator are the 'feed-forward' coefficients used to implement a real-time digital filter
.
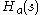is evaluated at 
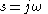which is on the 
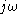axis. Likewise, to determine the frequency response of a discrete-time filter, the transfer function 
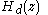is evaluated at 
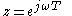which is on the unit circle, 
. When the actual frequency of 
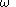is input to the discrete-time filter designed by use of the bilinear transform, it is desired to know at what frequency, 
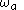, for the continuous-time filter that this 
is mapped to.
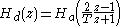
This shows that every point on the unit circle in the discrete-time filter z-plane,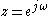
is mapped to a point on the 
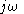axis on the continuous-time filter s-plane, 
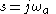. That is, the discrete-time to continuous-time frequency mapping of the bilinear transform is
and the inverse mapping is
The discrete-time filter behaves at frequency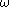
the same way that the continuous-time filter behaves at frequency 
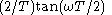. Specifically, the gain and phase shift that the discrete-time filter has at frequency 
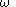is the same gain and phase shift that the continuous-time filter has at frequency 
. This means that every feature, every "bump" that is visible in the frequency response of the continuous-time filter is also visible in the discrete-time filter, but at a different frequency. For low frequencies (that is, when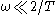 
or 
), 
.
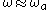One can see that the entire continuous frequency range
is mapped onto the fundamental frequency interval
The continuous-time filter frequency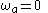
corresponds to the discrete-time filter frequency 
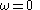and the continuous-time filter frequency 
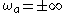correspond to the discrete-time filter frequency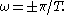 
One can also see that there is a nonlinear relationship between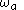
and 
This effect of the bilinear transform is called frequency warping. The continuous-time filter can be designed to compensate for this frequency warping by setting 
for every frequency specification that the designer has control over (such as corner frequency or center frequency). This is called pre-warping the filter design.
The main advantage of the warping phenomenon is the absence of aliasing distortion of the frequency response characteristic, such as observed with Impulse invariance
. It is necessary, however, to compensate for the frequency warping by pre-warping the given frequency specifications of the continuous-time system. These pre-warped specifications may then be used in the bilinear transform to obtain the desired discrete-time system.
Digital signal processing
Digital signal processing is concerned with the representation of discrete time signals by a sequence of numbers or symbols and the processing of these signals. Digital signal processing and analog signal processing are subfields of signal processing...
and discrete-time control theory
Control theory
Control theory is an interdisciplinary branch of engineering and mathematics that deals with the behavior of dynamical systems. The desired output of a system is called the reference...
to transform continuous-time system representations to discrete-time and vice versa.
The bilinear transform is a special case of a conformal map
Conformal map
In mathematics, a conformal map is a function which preserves angles. In the most common case the function is between domains in the complex plane.More formally, a map,...
ping (namely, the Möbius transformation), often used to convert a transfer function
Transfer function
A transfer function is a mathematical representation, in terms of spatial or temporal frequency, of the relation between the input and output of a linear time-invariant system. With optical imaging devices, for example, it is the Fourier transform of the point spread function i.e...
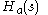of a linearLinear
In mathematics, a linear map or function f is a function which satisfies the following two properties:* Additivity : f = f + f...
, time-invariant (LTI
LTI system theory
Linear time-invariant system theory, commonly known as LTI system theory, comes from applied mathematics and has direct applications in NMR spectroscopy, seismology, circuits, signal processing, control theory, and other technical areas. It investigates the response of a linear and time-invariant...
) filter in the continuous
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
-time domain (often called an analog filter) to a transfer function
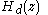of a linear, shift-invariant filter in the discreteDiscrete signal
A discrete signal or discrete-time signal is a time series consisting of a sequence of qualities...
-time domain (often called a digital filter
Digital filter
In electronics, computer science and mathematics, a digital filter is a system that performs mathematical operations on a sampled, discrete-time signal to reduce or enhance certain aspects of that signal. This is in contrast to the other major type of electronic filter, the analog filter, which is...
although there are analog filters constructed with switched capacitor
Switched capacitor
A switched capacitor is an electronic circuit element used for discrete time signal processing. It works by moving charges into and out of capacitors when switches are opened and closed. Usually, non-overlapping signals are used to control the switches, so that not all switches are closed...
s that are discrete-time filters). It maps positions on the
axis, , in the s-plane to the unit circleUnit circle
In mathematics, a unit circle is a circle with a radius of one. Frequently, especially in trigonometry, "the" unit circle is the circle of radius one centered at the origin in the Cartesian coordinate system in the Euclidean plane...
,
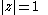, in the z-planeComplex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
. Other bilinear transforms can be used to warp the frequency response
Frequency response
Frequency response is the quantitative measure of the output spectrum of a system or device in response to a stimulus, and is used to characterize the dynamics of the system. It is a measure of magnitude and phase of the output as a function of frequency, in comparison to the input...
of any discrete-time linear system (for example to approximate the non-linear frequency resolution of the human auditory system) and are implementable in the discrete domain by replacing a system's unit delays
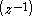with first order all-pass filterAll-pass filter
An all-pass filter is a signal processing filter that passes all frequencies equally, but changes the phase relationship between various frequencies. It does this by varying its propagation delay with frequency...
s.
The transform preserves stability
BIBO stability
In electrical engineering, specifically signal processing and control theory, BIBO stability is a form of stability for linear signals and systems that take inputs. BIBO stands for Bounded-Input Bounded-Output...
and maps every point of the frequency response
Frequency response
Frequency response is the quantitative measure of the output spectrum of a system or device in response to a stimulus, and is used to characterize the dynamics of the system. It is a measure of magnitude and phase of the output as a function of frequency, in comparison to the input...
of the continuous-time filter,
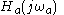to a corresponding point in the frequency response of the discrete-time filter, 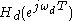although to a somewhat different frequency, as shown in the Frequency warping section below. This means that for every feature that one sees in the frequency response of the analog filter, there is a corresponding feature, with identical gain and phase shift, in the frequency response of the digital filter but, perhaps, at a somewhat different frequency. This is barely noticeable at low frequencies but is quite evident at frequencies close to the Nyquist frequencyNyquist frequency
The Nyquist frequency, named after the Swedish-American engineer Harry Nyquist or the Nyquist–Shannon sampling theorem, is half the sampling frequency of a discrete signal processing system...
.
Discrete-time approximation
The bilinear transform is a first-order approximation of the natural logarithm function that is an exact mapping of the z-plane to the s-plane. When the Laplace transform is performed on a discrete-time signal (with each element of the discrete-time sequence attached to a correspondingly delayed unit impulseDirac delta function
The Dirac delta function, or δ function, is a generalized function depending on a real parameter such that it is zero for all values of the parameter except when the parameter is zero, and its integral over the parameter from −∞ to ∞ is equal to one. It was introduced by theoretical...
), the result is precisely the Z transform of the discrete-time sequence with the substitution of
where
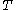is the numerical integrationNumerical integration
In numerical analysis, numerical integration constitutes a broad family of algorithms for calculating the numerical value of a definite integral, and by extension, the term is also sometimes used to describe the numerical solution of differential equations. This article focuses on calculation of...
step size of the trapezoidal rule used in the bilinear transform derivation. The above bilinear approximation can be solved for
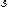or a similar approximation for 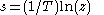can be performed.The inverse of this mapping (and its first-order bilinear approximation) is
The bilinear transform essentially uses this first order approximation and substitutes into the continuous-time transfer function,
That is
Stability and minimum-phase property preserved
A continuous-time causal filter is stableBIBO stability
In electrical engineering, specifically signal processing and control theory, BIBO stability is a form of stability for linear signals and systems that take inputs. BIBO stands for Bounded-Input Bounded-Output...
if the poles of its transfer function fall in the left half of the complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s-plane. A discrete-time causal filter is stable if the poles of its transfer function fall inside the unit circle
Unit circle
In mathematics, a unit circle is a circle with a radius of one. Frequently, especially in trigonometry, "the" unit circle is the circle of radius one centered at the origin in the Cartesian coordinate system in the Euclidean plane...
in the complex z-plane
Complex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
. The bilinear transform maps the left half of the complex s-plane to the interior of the unit circle in the z-plane. Thus filters designed in the continuous-time domain that are stable are converted to filters in the discrete-time domain that preserve that stability.
Likewise, a continuous-time filter is minimum-phase if the zeros
Zero (complex analysis)
In complex analysis, a zero of a holomorphic function f is a complex number a such that f = 0.-Multiplicity of a zero:A complex number a is a simple zero of f, or a zero of multiplicity 1 of f, if f can be written asf=g\,where g is a holomorphic function g such that g is not zero.Generally, the...
of its transfer function fall in the left half of the complex s-plane. A discrete-time filter is minimum-phase if the zeros of its transfer function fall inside the unit circle in the complex z-plane. Then the same mapping property assures that continuous-time filters that are minimum-phase are converted to discrete-time filters that preserve that property of being minimum-phase.
Example
As an example take a simple low-pass RC filter. This continuous-time filter has a transfer functionIf we wish to implement this filter as a digital filter, we can apply the bilinear transform by substituting for
the formula above; after some reworking, we get the following filter representation: |
 |
 |
|
 |
|
 |
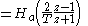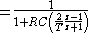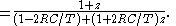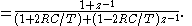The coefficients of the denominator are the 'feed-backward' coefficients and the coefficients of the numerator are the 'feed-forward' coefficients used to implement a real-time digital filter
Digital filter
In electronics, computer science and mathematics, a digital filter is a system that performs mathematical operations on a sampled, discrete-time signal to reduce or enhance certain aspects of that signal. This is in contrast to the other major type of electronic filter, the analog filter, which is...
.
Frequency warping
To determine the frequency response of a continuous-time filter, the transfer functionTransfer function
A transfer function is a mathematical representation, in terms of spatial or temporal frequency, of the relation between the input and output of a linear time-invariant system. With optical imaging devices, for example, it is the Fourier transform of the point spread function i.e...
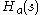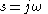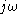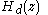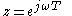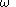is evaluated at which is on the axis. Likewise, to determine the frequency response of a discrete-time filter, the transfer function is evaluated at which is on the unit circle, . When the actual frequency of is input to the discrete-time filter designed by use of the bilinear transform, it is desired to know at what frequency, 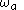, for the continuous-time filter that this is mapped to. |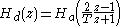
 |
 |
|
 |
|
 |
|
 |
|
 |
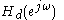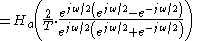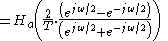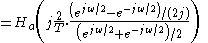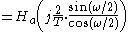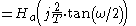This shows that every point on the unit circle in the discrete-time filter z-plane,
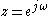is mapped to a point on the 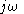axis on the continuous-time filter s-plane, 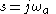. That is, the discrete-time to continuous-time frequency mapping of the bilinear transform isand the inverse mapping is
The discrete-time filter behaves at frequency
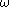the same way that the continuous-time filter behaves at frequency 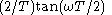. Specifically, the gain and phase shift that the discrete-time filter has at frequency 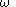is the same gain and phase shift that the continuous-time filter has at frequency . This means that every feature, every "bump" that is visible in the frequency response of the continuous-time filter is also visible in the discrete-time filter, but at a different frequency. For low frequencies (that is, when 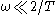or ), 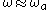.One can see that the entire continuous frequency range
is mapped onto the fundamental frequency interval
The continuous-time filter frequency
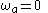corresponds to the discrete-time filter frequency 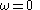and the continuous-time filter frequency 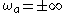correspond to the discrete-time filter frequency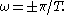 One can also see that there is a nonlinear relationship between
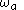and This effect of the bilinear transform is called frequency warping. The continuous-time filter can be designed to compensate for this frequency warping by setting for every frequency specification that the designer has control over (such as corner frequency or center frequency). This is called pre-warping the filter design.The main advantage of the warping phenomenon is the absence of aliasing distortion of the frequency response characteristic, such as observed with Impulse invariance
Impulse invariance
Impulse invariance is a technique for designing discrete-time infinite-impulse-response filters from continuous-time filters in which the impulse response of the continuous-time system is sampled to produce the impulse response of the discrete-time system...
. It is necessary, however, to compensate for the frequency warping by pre-warping the given frequency specifications of the continuous-time system. These pre-warped specifications may then be used in the bilinear transform to obtain the desired discrete-time system.