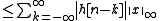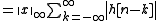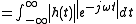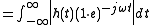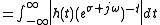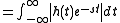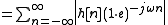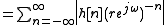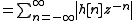BIBO stability
Encyclopedia
In electrical engineering
, specifically signal processing
and control theory
, BIBO stability is a form of stability for linear
signals and systems that take inputs. BIBO stands for Bounded-Input Bounded-Output. If a system is BIBO stable, then the output will be bounded for every input to the system that is bounded.
A signal is bounded if there is a finite value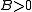 such that the signal magnitude never exceeds
such that the signal magnitude never exceeds  , that is
, that is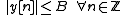 for discrete-time signals, or
for discrete-time signals, or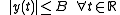 for continuous-time signals.
for continuous-time signals.
linear time invariant (LTI)
system, the condition for BIBO stability is that the impulse response
be absolutely integrable, i.e., its L1 norm
exist.

LTI system, the condition for BIBO stability is that the impulse response
be absolutely summable, i.e., its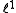 norm
norm
exist.
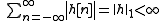
time LTI system with impulse response
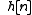 the relationship between the input
the relationship between the input 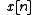 and the output
and the output 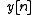 is
is
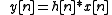
where denotes convolution
denotes convolution
.
Then it follows by the definition of convolution
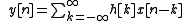
Let be the maximum value of
be the maximum value of 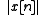 , i.e., the supremum norm
, i.e., the supremum norm
.
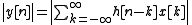
If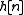 is absolutely summable, then
is absolutely summable, then  and
and
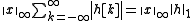
So if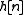 is absolutely summable and
is absolutely summable and  is bounded, then
is bounded, then  is bounded as well because
is bounded as well because  .
.
The proof for continuous-time follows the same arguments.
and continuous-time system
, the condition for stability is that the region of convergence (ROC) of the Laplace transform includes the imaginary axis
. When the system is causal
, the ROC is the open region to the right of a vertical line whose abscissa
is the real part of the "largest pole", or the pole that has the greatest real part of any pole in the system. The real part of the largest pole defining the ROC is called the abscissa of convergence. Therefore, all poles of the system must be in the strict left half of the s-plane for BIBO stability.
This stability condition can be derived from the above time-domain condition as follows :
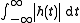
where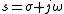 and
and 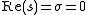 .
.
The region of convergence must therefore include the imaginary axis
.
and discrete time system
, the condition for stability is that the region of convergence (ROC) of the z-transform
includes the unit circle
. When the system is causal
, the ROC is the open region outside a circle whose radius is the magnitude of the pole with largest magnitude. Therefore, all poles of the system must be inside the unit circle
in the z-plane for BIBO stability.
This stability condition can be derived in a similar fashion to the continuous-time derivation:

where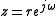 and
and  .
.
The region of convergence must therefore include the unit circle
.
Electrical engineering
Electrical engineering is a field of engineering that generally deals with the study and application of electricity, electronics and electromagnetism. The field first became an identifiable occupation in the late nineteenth century after commercialization of the electric telegraph and electrical...
, specifically signal processing
Signal processing
Signal processing is an area of systems engineering, electrical engineering and applied mathematics that deals with operations on or analysis of signals, in either discrete or continuous time...
and control theory
Control theory
Control theory is an interdisciplinary branch of engineering and mathematics that deals with the behavior of dynamical systems. The desired output of a system is called the reference...
, BIBO stability is a form of stability for linear
Linear system
A linear system is a mathematical model of a system based on the use of a linear operator.Linear systems typically exhibit features and properties that are much simpler than the general, nonlinear case....
signals and systems that take inputs. BIBO stands for Bounded-Input Bounded-Output. If a system is BIBO stable, then the output will be bounded for every input to the system that is bounded.
A signal is bounded if there is a finite value
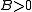 such that the signal magnitude never exceeds
such that the signal magnitude never exceeds  , that is
, that is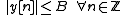 for discrete-time signals, or
for discrete-time signals, or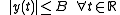 for continuous-time signals.
for continuous-time signals.Continuous-time necessary and sufficient condition
For a continuous timeContinuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
linear time invariant (LTI)
LTI system theory
Linear time-invariant system theory, commonly known as LTI system theory, comes from applied mathematics and has direct applications in NMR spectroscopy, seismology, circuits, signal processing, control theory, and other technical areas. It investigates the response of a linear and time-invariant...
system, the condition for BIBO stability is that the impulse response
Impulse response
In signal processing, the impulse response, or impulse response function , of a dynamic system is its output when presented with a brief input signal, called an impulse. More generally, an impulse response refers to the reaction of any dynamic system in response to some external change...
be absolutely integrable, i.e., its L1 norm
Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
exist.

Discrete-time sufficient condition
For a discrete timeDiscrete time
Discrete time is the discontinuity of a function's time domain that results from sampling a variable at a finite interval. For example, consider a newspaper that reports the price of crude oil once every day at 6:00AM. The newspaper is described as sampling the cost at a frequency of once per 24...
LTI system, the condition for BIBO stability is that the impulse response
Impulse response
In signal processing, the impulse response, or impulse response function , of a dynamic system is its output when presented with a brief input signal, called an impulse. More generally, an impulse response refers to the reaction of any dynamic system in response to some external change...
be absolutely summable, i.e., its
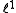 norm
normLp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
exist.
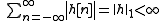
Proof of sufficiency
Given a discreteDiscrete mathematics
Discrete mathematics is the study of mathematical structures that are fundamentally discrete rather than continuous. In contrast to real numbers that have the property of varying "smoothly", the objects studied in discrete mathematics – such as integers, graphs, and statements in logic – do not...
time LTI system with impulse response
Impulse response
In signal processing, the impulse response, or impulse response function , of a dynamic system is its output when presented with a brief input signal, called an impulse. More generally, an impulse response refers to the reaction of any dynamic system in response to some external change...
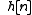 the relationship between the input
the relationship between the input 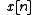 and the output
and the output 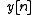 is
is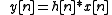
where
 denotes convolution
denotes convolutionConvolution
In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
.
Then it follows by the definition of convolution
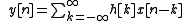
Let
 be the maximum value of
be the maximum value of 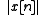 , i.e., the supremum norm
, i.e., the supremum normLp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
.
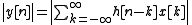
-
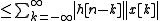 (by the triangle inequalityTriangle inequalityIn mathematics, the triangle inequality states that for any triangle, the sum of the lengths of any two sides must be greater than or equal to the length of the remaining side ....
(by the triangle inequalityTriangle inequalityIn mathematics, the triangle inequality states that for any triangle, the sum of the lengths of any two sides must be greater than or equal to the length of the remaining side ....
)
If
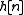 is absolutely summable, then
is absolutely summable, then  and
and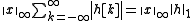
So if
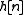 is absolutely summable and
is absolutely summable and  is bounded, then
is bounded, then  is bounded as well because
is bounded as well because  .
.The proof for continuous-time follows the same arguments.
Continuous-time signals
For a rationalRational function
In mathematics, a rational function is any function which can be written as the ratio of two polynomial functions. Neither the coefficients of the polynomials nor the values taken by the function are necessarily rational.-Definitions:...
and continuous-time system
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
, the condition for stability is that the region of convergence (ROC) of the Laplace transform includes the imaginary axis
Complex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
. When the system is causal
Causal system
A causal system is a system where the output depends on past/current inputs but not future inputs i.e...
, the ROC is the open region to the right of a vertical line whose abscissa
Abscissa
In mathematics, abscissa refers to that element of an ordered pair which is plotted on the horizontal axis of a two-dimensional Cartesian coordinate system, as opposed to the ordinate...
is the real part of the "largest pole", or the pole that has the greatest real part of any pole in the system. The real part of the largest pole defining the ROC is called the abscissa of convergence. Therefore, all poles of the system must be in the strict left half of the s-plane for BIBO stability.
This stability condition can be derived from the above time-domain condition as follows :
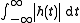
where
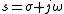 and
and 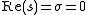 .
.The region of convergence must therefore include the imaginary axis
Complex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
.
Discrete-time signals
For a rationalRational function
In mathematics, a rational function is any function which can be written as the ratio of two polynomial functions. Neither the coefficients of the polynomials nor the values taken by the function are necessarily rational.-Definitions:...
and discrete time system
Discrete signal
A discrete signal or discrete-time signal is a time series consisting of a sequence of qualities...
, the condition for stability is that the region of convergence (ROC) of the z-transform
Z-transform
In mathematics and signal processing, the Z-transform converts a discrete time-domain signal, which is a sequence of real or complex numbers, into a complex frequency-domain representation....
includes the unit circle
Unit circle
In mathematics, a unit circle is a circle with a radius of one. Frequently, especially in trigonometry, "the" unit circle is the circle of radius one centered at the origin in the Cartesian coordinate system in the Euclidean plane...
. When the system is causal
Causal system
A causal system is a system where the output depends on past/current inputs but not future inputs i.e...
, the ROC is the open region outside a circle whose radius is the magnitude of the pole with largest magnitude. Therefore, all poles of the system must be inside the unit circle
Unit circle
In mathematics, a unit circle is a circle with a radius of one. Frequently, especially in trigonometry, "the" unit circle is the circle of radius one centered at the origin in the Cartesian coordinate system in the Euclidean plane...
in the z-plane for BIBO stability.
This stability condition can be derived in a similar fashion to the continuous-time derivation:

where
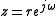 and
and  .
.The region of convergence must therefore include the unit circle
Unit circle
In mathematics, a unit circle is a circle with a radius of one. Frequently, especially in trigonometry, "the" unit circle is the circle of radius one centered at the origin in the Cartesian coordinate system in the Euclidean plane...
.
See also
- LTI system theoryLTI system theoryLinear time-invariant system theory, commonly known as LTI system theory, comes from applied mathematics and has direct applications in NMR spectroscopy, seismology, circuits, signal processing, control theory, and other technical areas. It investigates the response of a linear and time-invariant...
- Finite impulse response (FIR) filterFinite impulse responseA finite impulse response filter is a type of a signal processing filter whose impulse response is of finite duration, because it settles to zero in finite time. This is in contrast to infinite impulse response filters, which have internal feedback and may continue to respond indefinitely...
- Infinite impulse response (IIR) filterInfinite impulse responseInfinite impulse response is a property of signal processing systems. Systems with this property are known as IIR systems or, when dealing with filter systems, as IIR filters. IIR systems have an impulse response function that is non-zero over an infinite length of time...
- Nyquist plotNyquist plotA Nyquist plot is a parametric plot of a transfer function used in automatic control and signal processing. The most common use of Nyquist plots is for assessing the stability of a system with feedback. In Cartesian coordinates, the real part of the transfer function is plotted on the X axis. The...
- Routh-Hurwitz stability criterionRouth-Hurwitz stability criterionThe Routh–Hurwitz stability criterion is a necessary and sufficient method to establish the stability of a single-input, single-output , linear time invariant control system. More generally, given a polynomial, some calculations using only the coefficients of that polynomial can lead to the...
- Bode plot
- Phase marginPhase marginIn electronic amplifiers, phase margin is the difference between the phase, measured in degrees, of an amplifier's output signal and 180°, as a function of frequency. The PM is taken as positive at frequencies below where the open-loop phase first crosses 180°, i.e. the signal becomes inverted,...
- Root locus methodRoot locusRoot locus analysis is a graphical method for examining how the roots of a system change with variation of a certain system parameter, commonly the gain of a feedback system. This is a technique used in the field of control systems developed by Walter R...
Further reading
- Gordon E. Carlson Signal and Linear Systems Analysis with Matlab second edition, Wiley, 1998, ISBN 0-471-12465-6
- John G. Proakis and Dimitris G. Manolakis Digital Signal Processing Principals, Algorithms and Applications third edition, Prentice Hall, 1996, ISBN 0-13-373762-4
- D. Ronald Fannin, William H. Tranter, and Rodger E. Ziemer Signals & Systems Continuous and Discrete fourth edition, Prentice Hall, 1998, ISBN 0-13-496456-X
- Proof of the necessary conditions for BIBO stability.