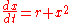
Saddle-node bifurcation
Encyclopedia
In the mathematical
area of bifurcation theory
a saddle-node bifurcation, tangential bifurcation or fold bifurcation is a local bifurcation in which two fixed point
s (or equilibria) of a dynamical system
collide and annihilate each other. The term 'saddle-node bifurcation' is most often used in reference to continuous dynamical systems. In discrete dynamical systems, the same bifurcation is often instead called a fold bifurcation. Another name is blue skies bifurcation in reference to the sudden creation of two fixed points.
If the phase space is one-dimensional, one of the equilibrium points is unstable (the saddle), while the other is stable (the node).
The normal form of a saddle-node bifurcation is:
Here is the state variable and
is the state variable and  is the bifurcation parameter.
is the bifurcation parameter.
A saddle-node bifurcation occurs in the consumer equation (see transcritical bifurcation
) if the consumption term is changed from to
to 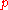 , that is the consumption rate is constant and not in proportion to resource
, that is the consumption rate is constant and not in proportion to resource  .
.
Saddle-node bifurcations may be associated with hysteresis loops
and catastrophes
.
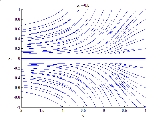
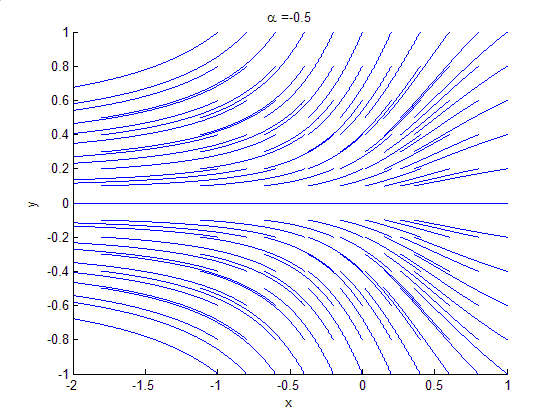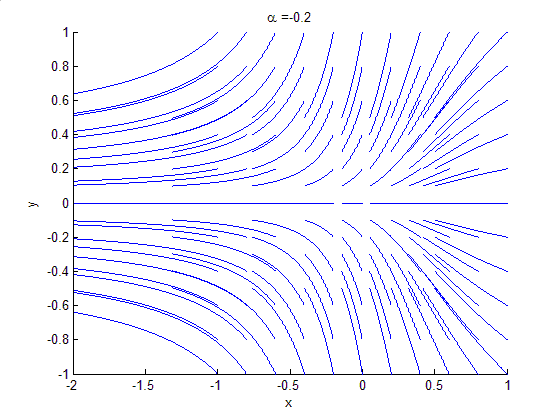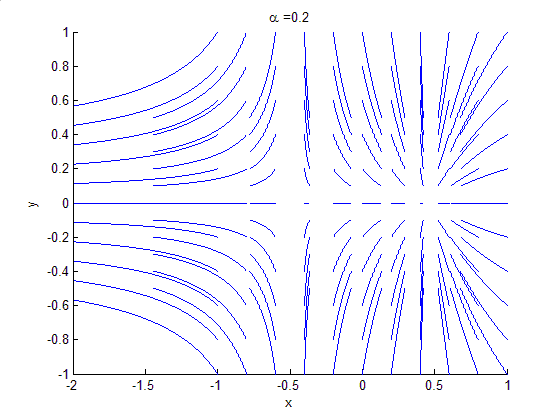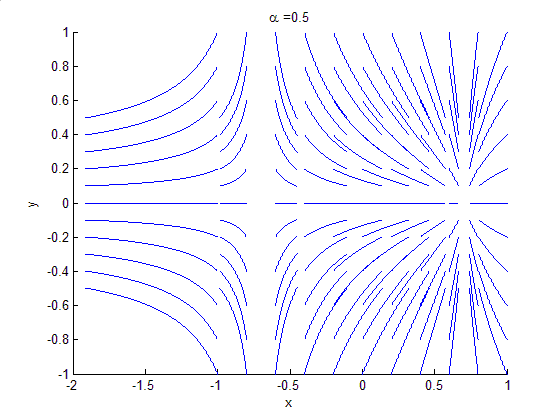 An example of a saddle-node bifurcation in two-dimensions occurs in the two-dimensional dynamical system:
An example of a saddle-node bifurcation in two-dimensions occurs in the two-dimensional dynamical system:
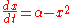

As can be seen by the animation obtained by plotting phase portraits by varying the parameter ,
,
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
area of bifurcation theory
Bifurcation theory
Bifurcation theory is the mathematical study of changes in the qualitative or topological structure of a given family, such as the integral curves of a family of vector fields, and the solutions of a family of differential equations...
a saddle-node bifurcation, tangential bifurcation or fold bifurcation is a local bifurcation in which two fixed point
Fixed point (mathematics)
In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...
s (or equilibria) of a dynamical system
Dynamical system
A dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
collide and annihilate each other. The term 'saddle-node bifurcation' is most often used in reference to continuous dynamical systems. In discrete dynamical systems, the same bifurcation is often instead called a fold bifurcation. Another name is blue skies bifurcation in reference to the sudden creation of two fixed points.
If the phase space is one-dimensional, one of the equilibrium points is unstable (the saddle), while the other is stable (the node).
The normal form of a saddle-node bifurcation is:
Here
 is the state variable and
is the state variable and  is the bifurcation parameter.
is the bifurcation parameter.
- If
 there are two equilibrium points, a stable equilibrium point at
there are two equilibrium points, a stable equilibrium point at  and an unstable one at
and an unstable one at  .
. - At
 (the bifurcation point) there is exactly one equilibrium point. At this point the fixed point is no longer hyperbolic. In this case the fixed point is called a saddle-node fixed point.
(the bifurcation point) there is exactly one equilibrium point. At this point the fixed point is no longer hyperbolic. In this case the fixed point is called a saddle-node fixed point. - If
 there are no equilibrium points.
there are no equilibrium points.
A saddle-node bifurcation occurs in the consumer equation (see transcritical bifurcation
Transcritical bifurcation
In bifurcation theory, a field within mathematics, a transcritical bifurcation is a particular kind of local bifurcation, meaning that it is characterized by an equilibrium having an eigenvalue whose real part passes through zero....
) if the consumption term is changed from
 to
to 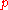 , that is the consumption rate is constant and not in proportion to resource
, that is the consumption rate is constant and not in proportion to resource  .
.Saddle-node bifurcations may be associated with hysteresis loops
Hysteresis
Hysteresis is the dependence of a system not just on its current environment but also on its past. This dependence arises because the system can be in more than one internal state. To predict its future evolution, either its internal state or its history must be known. If a given input alternately...
and catastrophes
Catastrophe theory
In mathematics, catastrophe theory is a branch of bifurcation theory in the study of dynamical systems; it is also a particular special case of more general singularity theory in geometry....
.
Example

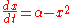

As can be seen by the animation obtained by plotting phase portraits by varying the parameter
 ,
,- When
 is negative, there are no equilibrium points.
is negative, there are no equilibrium points. - When
 , there is a saddle-node point.
, there is a saddle-node point. - When
 is positive, there are two equilibrium points: that is, one saddle pointSaddle pointIn mathematics, a saddle point is a point in the domain of a function that is a stationary point but not a local extremum. The name derives from the fact that in two dimensions the surface resembles a saddle that curves up in one direction, and curves down in a different direction...
is positive, there are two equilibrium points: that is, one saddle pointSaddle pointIn mathematics, a saddle point is a point in the domain of a function that is a stationary point but not a local extremum. The name derives from the fact that in two dimensions the surface resembles a saddle that curves up in one direction, and curves down in a different direction...
and one node (either an attractor or a repellor),.
See also
- Pitchfork bifurcationPitchfork bifurcationIn bifurcation theory, a field within mathematics, a pitchfork bifurcation is a particular type of local bifurcation. Pitchfork bifurcations, like Hopf bifurcations have two types - supercritical or subcritical....
- Transcritical bifurcationTranscritical bifurcationIn bifurcation theory, a field within mathematics, a transcritical bifurcation is a particular kind of local bifurcation, meaning that it is characterized by an equilibrium having an eigenvalue whose real part passes through zero....
- Hopf bifurcationHopf bifurcationIn the mathematical theory of bifurcations, a Hopf or Poincaré–Andronov–Hopf bifurcation, named after Henri Poincaré, Eberhard Hopf, and Aleksandr Andronov, is a local bifurcation in which a fixed point of a dynamical system loses stability as a pair of complex conjugate eigenvalues of...
- Saddle pointSaddle pointIn mathematics, a saddle point is a point in the domain of a function that is a stationary point but not a local extremum. The name derives from the fact that in two dimensions the surface resembles a saddle that curves up in one direction, and curves down in a different direction...