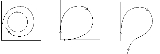
Homoclinic bifurcation
Encyclopedia
In mathematics
, a homoclinic bifurcation is a global bifurcation which often occurs when a periodic orbit collides with a saddle point
.
The image below shows a phase portrait before, at, and after a homoclinic bifurcation in 2D. The periodic orbit grows until it collides with the saddle point. At the bifurcation point the period of the periodic orbit has grown to infinity and it has become a homoclinic orbit
. After the bifurcation there is no longer a periodic orbit.
Homoclinic bifurcations can occur supercritically or subcritically. The variant above is the "small" or "type I" homoclinic bifurcation.
In 2D there is also the "big" or "type II" homoclinic bifurcation in which the homoclinic orbit "traps" the other ends of the unstable and stable manifolds of the saddle. In three or more dimensions, higher codimension bifurcations can occur, producing complicated, possibly chaotic
dynamics.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a homoclinic bifurcation is a global bifurcation which often occurs when a periodic orbit collides with a saddle point
Saddle point
In mathematics, a saddle point is a point in the domain of a function that is a stationary point but not a local extremum. The name derives from the fact that in two dimensions the surface resembles a saddle that curves up in one direction, and curves down in a different direction...
.
The image below shows a phase portrait before, at, and after a homoclinic bifurcation in 2D. The periodic orbit grows until it collides with the saddle point. At the bifurcation point the period of the periodic orbit has grown to infinity and it has become a homoclinic orbit
Homoclinic orbit
In mathematics, a homoclinic orbit is a trajectory of a flow of a dynamical system which joins a saddle equilibrium point to itself. More precisely, a homoclinic orbit lies in the intersection of the stable manifold and the unstable manifold of an equilibrium.Homoclinic orbits and homoclinic points...
. After the bifurcation there is no longer a periodic orbit.
In 2D there is also the "big" or "type II" homoclinic bifurcation in which the homoclinic orbit "traps" the other ends of the unstable and stable manifolds of the saddle. In three or more dimensions, higher codimension bifurcations can occur, producing complicated, possibly chaotic
Chaos theory
Chaos theory is a field of study in mathematics, with applications in several disciplines including physics, economics, biology, and philosophy. Chaos theory studies the behavior of dynamical systems that are highly sensitive to initial conditions, an effect which is popularly referred to as the...
dynamics.