
Bertrand's theorem
Encyclopedia
In classical mechanics
, Bertrand's theorem states that only two types of central force potential
s produce stable, closed orbits
: (1) an inverse-square central force such as the gravitational or electrostatic potential
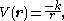
and (2) the radial harmonic oscillator potential
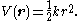
orbits, which are naturally closed orbits
. The only requirement is that the central force exactly equals the centripetal force requirement
, which determines the required angular velocity for a given circular radius. Non-central forces (i.e., those that depend on the angular variables as well as the radius) are ignored here, since they do not produce circular orbits in general.
The equation of motion for the radius of a particle
of a particle
of mass moving in a central potential
moving in a central potential 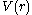 is given by Lagrange's equations
is given by Lagrange's equations
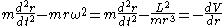
where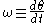 and the angular momentum
and the angular momentum
 is conserved. For illustration, the first term on the left-hand side is zero for circular orbits, and the applied inwards force
is conserved. For illustration, the first term on the left-hand side is zero for circular orbits, and the applied inwards force 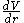 equals the centripetal force requirement
equals the centripetal force requirement
 , as expected.
, as expected.
The definition of angular momentum
allows a change of independent variable from to
to 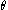
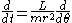
giving the new equation of motion that is independent of time
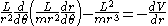
This equation becomes quasilinear on making the change of variables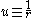 and multiplying both sides by
and multiplying both sides by  (see also Binet equation
(see also Binet equation
)

given an appropriate initial velocity. However, if some radial velocity is introduced, these orbits need not be stable (i.e., remain in orbit indefinitely) nor closed (repeatedly returning to exactly the same path). Here we show that stable, exactly closed orbits can be produced only with an inverse-square force or radial harmonic oscillator potential (a necessary condition
). In the following sections, we show that those force laws do produce stable, exactly closed orbits
(a sufficient condition
).
Define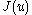 as
as
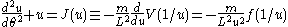
where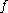 represents the radial force. The criterion for perfectly circular
represents the radial force. The criterion for perfectly circular
motion at a radius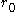 is that the first term on the left-hand side be zero
is that the first term on the left-hand side be zero
where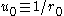 .
.
The next step is to consider the equation for under small perturbations
under small perturbations
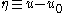 from perfectly circular orbits. On the right-hand side, the
from perfectly circular orbits. On the right-hand side, the 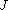 function can be expanded in a standard Taylor series
function can be expanded in a standard Taylor series
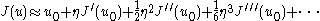
Substituting this expansion into the equation for and subtracting the constant terms yields
and subtracting the constant terms yields
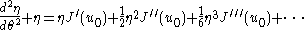
which can be written as
where is a constant.
is a constant. 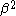 must be non-negative; otherwise, the radius of the orbit would vary exponentially away from its initial radius. (The solution
must be non-negative; otherwise, the radius of the orbit would vary exponentially away from its initial radius. (The solution  corresponds to a perfectly circular orbit.) If the right-hand side may be neglected (i.e., for small perturbations), the solutions are
corresponds to a perfectly circular orbit.) If the right-hand side may be neglected (i.e., for small perturbations), the solutions are
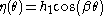
where the amplitude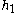 is a constant of integration. For the orbits to be closed,
is a constant of integration. For the orbits to be closed,  must be a rational number
must be a rational number
. What's more, it must be the same rational number for all radii, since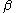 cannot change continuously; the rational number
cannot change continuously; the rational number
s are totally disconnected
from one another. Using the definition of along with equation (1),
along with equation (1),
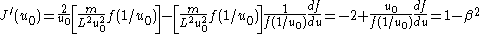
where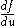 is evaluated at
is evaluated at 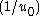 . Since this must hold for any value of
. Since this must hold for any value of  ,
,
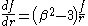
which implies that the force must follow a power law
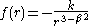
Hence,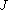 must have the general form
must have the general form
For more general deviations from circularity (i.e., when we cannot neglect the higher order terms in the Taylor expansion of ),
),  may be expanded in a Fourier series, e.g.,
may be expanded in a Fourier series, e.g.,
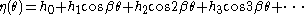
We substitute this into equation (2) and equate the coefficients belonging to the same frequency, keeping only the lowest order terms. As we show below,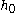 and
and 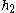 are smaller than
are smaller than 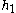 , being of order
, being of order 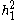 .
. 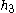 , and all further coefficients, are at least of order
, and all further coefficients, are at least of order 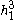 . This makes sense since
. This makes sense since 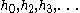 must all vanish faster than
must all vanish faster than 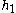 as a circular orbit is approached.
as a circular orbit is approached.
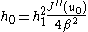
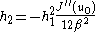
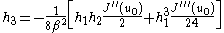
From the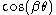 term, we get
term, we get
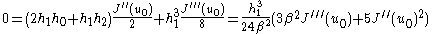
where in the last step we substituted in the values of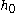 and
and 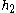 .
.
Using equations (3) and (1), we can calculate the second and third derivatives of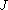 evaluated at
evaluated at 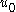 ,
,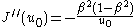

Substituting these values into the last equation yields the main result of Bertrand's theorem
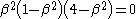
Hence, the only potential
s that can produce stable, closed, non-circular orbits are the inverse-square force law (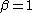 ) and the radial harmonic oscillator potential (
) and the radial harmonic oscillator potential (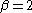 ). The solution
). The solution 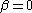 corresponds to perfectly circular orbits, as noted above.
corresponds to perfectly circular orbits, as noted above.
, the potential
can be written
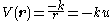
The orbit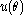 can be derived from the general equation
can be derived from the general equation
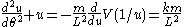
whose solution is the constant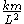 plus a simple sinusoid
plus a simple sinusoid

where (the eccentricity) and
(the eccentricity) and 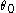 (the phase offset) are constants of integration.
(the phase offset) are constants of integration.
This is the general formula for a conic section
that has one focus at the origin;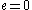 corresponds to a circle
corresponds to a circle
, corresponds to an ellipse,
corresponds to an ellipse, 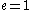 corresponds to a parabola
corresponds to a parabola
, and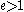 corresponds to a hyperbola
corresponds to a hyperbola
. The eccentricity is related to the total energy
is related to the total energy
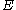 (cf. the Laplace–Runge–Lenz vector)
(cf. the Laplace–Runge–Lenz vector)
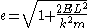
Comparing these formulae shows that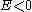 corresponds to an ellipse,
corresponds to an ellipse,  corresponds to a parabola
corresponds to a parabola
, and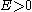 corresponds to a hyperbola
corresponds to a hyperbola
. In particular,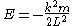 for perfectly circular
for perfectly circular
orbits.
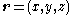 . The potential energy can be written
. The potential energy can be written
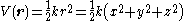
The equation of motion for a particle of mass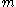 is given by three independent Lagrange's equations
is given by three independent Lagrange's equations
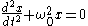
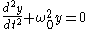

where the constant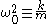 must be positive (i.e.,
must be positive (i.e., 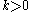 ) to ensure bounded, closed orbits; otherwise, the particle will fly off to infinity
) to ensure bounded, closed orbits; otherwise, the particle will fly off to infinity
. The solutions of these simple harmonic oscillator equations are all similar
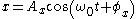
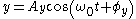
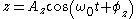
where the positive constants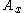 ,
, 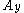 and
and 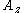 represent the amplitudes of the oscillations and the angles
represent the amplitudes of the oscillations and the angles 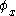 ,
, 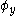 and
and 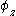 represent their phases. The resulting orbit
represent their phases. The resulting orbit
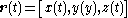 is closed because it repeats exactly after a period
is closed because it repeats exactly after a period
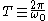
The system is also stable because small perturbations in the amplitudes and phases cause correspondingly small changes in the overall orbit.
Classical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
, Bertrand's theorem states that only two types of central force potential
Potential
*In linguistics, the potential mood*The mathematical study of potentials is known as potential theory; it is the study of harmonic functions on manifolds...
s produce stable, closed orbits
Orbit (dynamics)
In mathematics, in the study of dynamical systems, an orbit is a collection of points related by the evolution function of the dynamical system. The orbit is a subset of the phase space and the set of all orbits is a partition of the phase space, that is different orbits do not intersect in the...
: (1) an inverse-square central force such as the gravitational or electrostatic potential
Electrostatics
Electrostatics is the branch of physics that deals with the phenomena and properties of stationary or slow-moving electric charges....
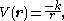
and (2) the radial harmonic oscillator potential
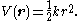
General preliminaries
All attractive central forces can produce circularCircle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
orbits, which are naturally closed orbits
Orbit (dynamics)
In mathematics, in the study of dynamical systems, an orbit is a collection of points related by the evolution function of the dynamical system. The orbit is a subset of the phase space and the set of all orbits is a partition of the phase space, that is different orbits do not intersect in the...
. The only requirement is that the central force exactly equals the centripetal force requirement
Centripetal force
Centripetal force is a force that makes a body follow a curved path: it is always directed orthogonal to the velocity of the body, toward the instantaneous center of curvature of the path. The mathematical description was derived in 1659 by Dutch physicist Christiaan Huygens...
, which determines the required angular velocity for a given circular radius. Non-central forces (i.e., those that depend on the angular variables as well as the radius) are ignored here, since they do not produce circular orbits in general.
The equation of motion for the radius
 of a particle
of a particleof mass
 moving in a central potential
moving in a central potential 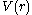 is given by Lagrange's equations
is given by Lagrange's equationsEuler-Lagrange equation
In calculus of variations, the Euler–Lagrange equation, Euler's equation, or Lagrange's equation, is a differential equation whose solutions are the functions for which a given functional is stationary...
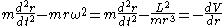
where
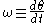 and the angular momentum
and the angular momentumAngular momentum
In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
 is conserved. For illustration, the first term on the left-hand side is zero for circular orbits, and the applied inwards force
is conserved. For illustration, the first term on the left-hand side is zero for circular orbits, and the applied inwards force 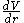 equals the centripetal force requirement
equals the centripetal force requirementCentripetal force
Centripetal force is a force that makes a body follow a curved path: it is always directed orthogonal to the velocity of the body, toward the instantaneous center of curvature of the path. The mathematical description was derived in 1659 by Dutch physicist Christiaan Huygens...
 , as expected.
, as expected.The definition of angular momentum
Angular momentum
In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
allows a change of independent variable from
 to
to 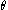
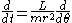
giving the new equation of motion that is independent of time
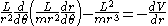
This equation becomes quasilinear on making the change of variables
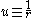 and multiplying both sides by
and multiplying both sides by  (see also Binet equation
(see also Binet equationBinet equation
The Binet equation, derived by Jacques Philippe Marie Binet, provides the form of a central force given the shape of the orbital motion in plane polar coordinates. The equation can also be used to derive the shape of the orbit for a given force law, but this usually involves the solution to a...
)

Bertrand's theorem
As noted above, all central forces can produce circular orbitsOrbit (dynamics)
In mathematics, in the study of dynamical systems, an orbit is a collection of points related by the evolution function of the dynamical system. The orbit is a subset of the phase space and the set of all orbits is a partition of the phase space, that is different orbits do not intersect in the...
given an appropriate initial velocity. However, if some radial velocity is introduced, these orbits need not be stable (i.e., remain in orbit indefinitely) nor closed (repeatedly returning to exactly the same path). Here we show that stable, exactly closed orbits can be produced only with an inverse-square force or radial harmonic oscillator potential (a necessary condition
Necessary and sufficient conditions
In logic, the words necessity and sufficiency refer to the implicational relationships between statements. The assertion that one statement is a necessary and sufficient condition of another means that the former statement is true if and only if the latter is true.-Definitions:A necessary condition...
). In the following sections, we show that those force laws do produce stable, exactly closed orbits
Orbit (dynamics)
In mathematics, in the study of dynamical systems, an orbit is a collection of points related by the evolution function of the dynamical system. The orbit is a subset of the phase space and the set of all orbits is a partition of the phase space, that is different orbits do not intersect in the...
(a sufficient condition
Necessary and sufficient conditions
In logic, the words necessity and sufficiency refer to the implicational relationships between statements. The assertion that one statement is a necessary and sufficient condition of another means that the former statement is true if and only if the latter is true.-Definitions:A necessary condition...
).
Define
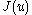 as
as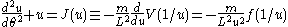
where
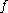 represents the radial force. The criterion for perfectly circular
represents the radial force. The criterion for perfectly circularCircle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
motion at a radius
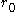 is that the first term on the left-hand side be zero
is that the first term on the left-hand side be zerowhere
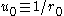 .
.The next step is to consider the equation for
 under small perturbations
under small perturbationsPerturbation theory
Perturbation theory comprises mathematical methods that are used to find an approximate solution to a problem which cannot be solved exactly, by starting from the exact solution of a related problem...
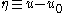 from perfectly circular orbits. On the right-hand side, the
from perfectly circular orbits. On the right-hand side, the 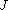 function can be expanded in a standard Taylor series
function can be expanded in a standard Taylor seriesTaylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
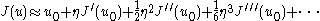
Substituting this expansion into the equation for
 and subtracting the constant terms yields
and subtracting the constant terms yields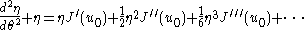
which can be written as
where
 is a constant.
is a constant. 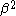 must be non-negative; otherwise, the radius of the orbit would vary exponentially away from its initial radius. (The solution
must be non-negative; otherwise, the radius of the orbit would vary exponentially away from its initial radius. (The solution  corresponds to a perfectly circular orbit.) If the right-hand side may be neglected (i.e., for small perturbations), the solutions are
corresponds to a perfectly circular orbit.) If the right-hand side may be neglected (i.e., for small perturbations), the solutions are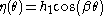
where the amplitude
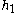 is a constant of integration. For the orbits to be closed,
is a constant of integration. For the orbits to be closed,  must be a rational number
must be a rational numberRational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
. What's more, it must be the same rational number for all radii, since
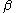 cannot change continuously; the rational number
cannot change continuously; the rational numberRational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s are totally disconnected
Totally disconnected space
In topology and related branches of mathematics, a totally disconnected space is a topological space that is maximally disconnected, in the sense that it has no non-trivial connected subsets...
from one another. Using the definition of
 along with equation (1),
along with equation (1),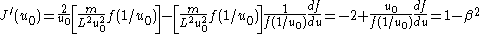
where
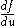 is evaluated at
is evaluated at 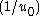 . Since this must hold for any value of
. Since this must hold for any value of  ,
,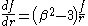
which implies that the force must follow a power law
Power law
A power law is a special kind of mathematical relationship between two quantities. When the frequency of an event varies as a power of some attribute of that event , the frequency is said to follow a power law. For instance, the number of cities having a certain population size is found to vary...
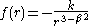
Hence,
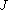 must have the general form
must have the general formFor more general deviations from circularity (i.e., when we cannot neglect the higher order terms in the Taylor expansion of
 ),
),  may be expanded in a Fourier series, e.g.,
may be expanded in a Fourier series, e.g.,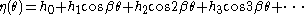
We substitute this into equation (2) and equate the coefficients belonging to the same frequency, keeping only the lowest order terms. As we show below,
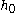 and
and 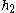 are smaller than
are smaller than 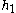 , being of order
, being of order 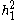 .
. 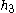 , and all further coefficients, are at least of order
, and all further coefficients, are at least of order 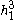 . This makes sense since
. This makes sense since 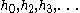 must all vanish faster than
must all vanish faster than 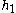 as a circular orbit is approached.
as a circular orbit is approached.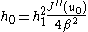
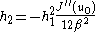
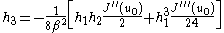
From the
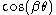 term, we get
term, we get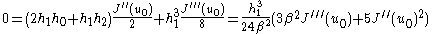
where in the last step we substituted in the values of
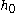 and
and 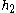 .
.Using equations (3) and (1), we can calculate the second and third derivatives of
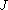 evaluated at
evaluated at 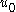 ,
,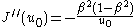

Substituting these values into the last equation yields the main result of Bertrand's theorem
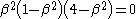
Hence, the only potential
Potential
*In linguistics, the potential mood*The mathematical study of potentials is known as potential theory; it is the study of harmonic functions on manifolds...
s that can produce stable, closed, non-circular orbits are the inverse-square force law (
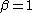 ) and the radial harmonic oscillator potential (
) and the radial harmonic oscillator potential (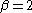 ). The solution
). The solution 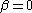 corresponds to perfectly circular orbits, as noted above.
corresponds to perfectly circular orbits, as noted above.Inverse-square force (Kepler problem)
For an inverse-square force law such as the gravitational or electrostatic potentialElectrostatics
Electrostatics is the branch of physics that deals with the phenomena and properties of stationary or slow-moving electric charges....
, the potential
Potential
*In linguistics, the potential mood*The mathematical study of potentials is known as potential theory; it is the study of harmonic functions on manifolds...
can be written
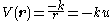
The orbit
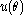 can be derived from the general equation
can be derived from the general equation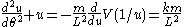
whose solution is the constant
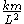 plus a simple sinusoid
plus a simple sinusoid
where
 (the eccentricity) and
(the eccentricity) and 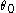 (the phase offset) are constants of integration.
(the phase offset) are constants of integration.This is the general formula for a conic section
Conic section
In mathematics, a conic section is a curve obtained by intersecting a cone with a plane. In analytic geometry, a conic may be defined as a plane algebraic curve of degree 2...
that has one focus at the origin;
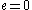 corresponds to a circle
corresponds to a circleCircle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
,
 corresponds to an ellipse,
corresponds to an ellipse, 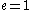 corresponds to a parabola
corresponds to a parabolaParabola
In mathematics, the parabola is a conic section, the intersection of a right circular conical surface and a plane parallel to a generating straight line of that surface...
, and
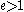 corresponds to a hyperbola
corresponds to a hyperbolaHyperbola
In mathematics a hyperbola is a curve, specifically a smooth curve that lies in a plane, which can be defined either by its geometric properties or by the kinds of equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, which are mirror...
. The eccentricity
 is related to the total energy
is related to the total energyEnergy
In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
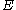 (cf. the Laplace–Runge–Lenz vector)
(cf. the Laplace–Runge–Lenz vector)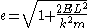
Comparing these formulae shows that
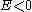 corresponds to an ellipse,
corresponds to an ellipse,  corresponds to a parabola
corresponds to a parabolaParabola
In mathematics, the parabola is a conic section, the intersection of a right circular conical surface and a plane parallel to a generating straight line of that surface...
, and
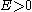 corresponds to a hyperbola
corresponds to a hyperbolaHyperbola
In mathematics a hyperbola is a curve, specifically a smooth curve that lies in a plane, which can be defined either by its geometric properties or by the kinds of equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, which are mirror...
. In particular,
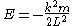 for perfectly circular
for perfectly circularCircle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
orbits.
Radial harmonic oscillator
To solve for the orbit under a radial harmonic oscillator potential, it's easier to work in components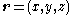 . The potential energy can be written
. The potential energy can be written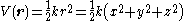
The equation of motion for a particle of mass
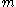 is given by three independent Lagrange's equations
is given by three independent Lagrange's equationsEuler-Lagrange equation
In calculus of variations, the Euler–Lagrange equation, Euler's equation, or Lagrange's equation, is a differential equation whose solutions are the functions for which a given functional is stationary...
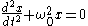
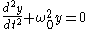

where the constant
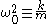 must be positive (i.e.,
must be positive (i.e., 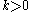 ) to ensure bounded, closed orbits; otherwise, the particle will fly off to infinity
) to ensure bounded, closed orbits; otherwise, the particle will fly off to infinityInfinity
Infinity is a concept in many fields, most predominantly mathematics and physics, that refers to a quantity without bound or end. People have developed various ideas throughout history about the nature of infinity...
. The solutions of these simple harmonic oscillator equations are all similar
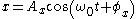
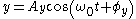
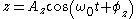
where the positive constants
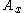 ,
, 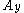 and
and 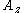 represent the amplitudes of the oscillations and the angles
represent the amplitudes of the oscillations and the angles 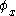 ,
, 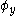 and
and 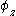 represent their phases. The resulting orbit
represent their phases. The resulting orbit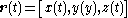 is closed because it repeats exactly after a period
is closed because it repeats exactly after a period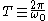
The system is also stable because small perturbations in the amplitudes and phases cause correspondingly small changes in the overall orbit.
Further reading
- Goldstein H. (1980) Classical Mechanics, 2nd. ed., Addison-Wesley. ISBN 0-201-02918-9
- :lt:Bertrano teorema Bertrano teorema (lietuviškai)

