Circular segment
Encyclopedia
In geometry
, a circular segment is an area of a circle
informally defined as an area which is "cut off" from the rest of the circle by a secant
or a chord
. The circle segment constitutes the part between the secant and an arc, excluding the circle's center. This is commonly known as Meglio's Area.
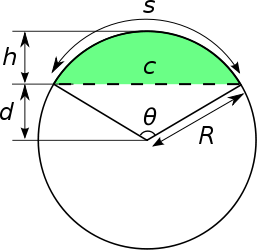 Let R be the radius
Let R be the radius
of the circle
, θ is the central angle in radians, α is the central angle in degrees, c the chord length
, s the arc length, h the height
of the segment, and d the height of the triangular
portion.
of the circular segment is equal to the area of the circular sector
minus the area of the triangular portion.

It should be noted that theta in this equation is in radians. For theta in degrees the following modification should be added:

This method can also be used to find the angle ½ of the segment, by measuring the angle between the two above mentioned rulers.
of the segment, by measuring the angle between the two above mentioned rulers.
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, a circular segment is an area of a circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
informally defined as an area which is "cut off" from the rest of the circle by a secant
Secant line
A secant line of a curve is a line that intersects two points on the curve. The word secant comes from the Latin secare, to cut.It can be used to approximate the tangent to a curve, at some point P...
or a chord
Chord (geometry)
A chord of a circle is a geometric line segment whose endpoints both lie on the circumference of the circle.A secant or a secant line is the line extension of a chord. More generally, a chord is a line segment joining two points on any curve, such as but not limited to an ellipse...
. The circle segment constitutes the part between the secant and an arc, excluding the circle's center. This is commonly known as Meglio's Area.
Formulas

Radius
In classical geometry, a radius of a circle or sphere is any line segment from its center to its perimeter. By extension, the radius of a circle or sphere is the length of any such segment, which is half the diameter. If the object does not have an obvious center, the term may refer to its...
of the circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
, θ is the central angle in radians, α is the central angle in degrees, c the chord length
Length
In geometric measurements, length most commonly refers to the longest dimension of an object.In certain contexts, the term "length" is reserved for a certain dimension of an object along which the length is measured. For example it is possible to cut a length of a wire which is shorter than wire...
, s the arc length, h the height
Height
Height is the measurement of vertical distance, but has two meanings in common use. It can either indicate how "tall" something is, or how "high up" it is. For example "The height of the building is 50 m" or "The height of the airplane is 10,000 m"...
of the segment, and d the height of the triangular
Triangle
A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
portion.
- The radius is

- The arc length is

- The chord length is

- The height is

- The angle is

Area
The areaArea
Area is a quantity that expresses the extent of a two-dimensional surface or shape in the plane. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat...
of the circular segment is equal to the area of the circular sector
Circular sector
A circular sector or circle sector, is the portion of a disk enclosed by two radii and an arc, where the smaller area is known as the minor sector and the larger being the major sector. In the diagram, θ is the central angle in radians, r the radius of the circle, and L is the arc length of the...
minus the area of the triangular portion.

It should be noted that theta in this equation is in radians. For theta in degrees the following modification should be added:

Radius
A way of approaching the radius of a Circular segment with only the chord and height of the segment is the Pietrow-Vollema Radius method. This method uses the constant length of the radius of a circle as a way of finding it. One can find the radius by recreating the shape of the included picture, with two or three rulers. Meaning that the first ruler is set to zero on point C, and the other on point B. Then by crossing the rulers one can find the exact point of intersection where both of the rulers have back the same length. Thus the radius of the circle.This method can also be used to find the angle ½
 of the segment, by measuring the angle between the two above mentioned rulers.
of the segment, by measuring the angle between the two above mentioned rulers.See also
- Circular sectorCircular sectorA circular sector or circle sector, is the portion of a disk enclosed by two radii and an arc, where the smaller area is known as the minor sector and the larger being the major sector. In the diagram, θ is the central angle in radians, r the radius of the circle, and L is the arc length of the...
- ArcArc (geometry)In geometry, an arc is a closed segment of a differentiable curve in the two-dimensional plane; for example, a circular arc is a segment of the circumference of a circle...
- Conic sectionConic sectionIn mathematics, a conic section is a curve obtained by intersecting a cone with a plane. In analytic geometry, a conic may be defined as a plane algebraic curve of degree 2...
- Cross sectionCross section (geometry)In geometry, a cross-section is the intersection of a figure in 2-dimensional space with a line, or of a body in 3-dimensional space with a plane, etc...
External links
- Definition of a circular segment With interactive animation
- Formulae for area of a circular segment With interactive animation

