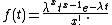Telescoping series
Encyclopedia
In mathematics
, a telescoping series is a series
whose partial sums eventually only have a fixed number of terms after cancellation. Such a technique is also known as the method of differences.
For example, the series
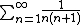
simplifies as
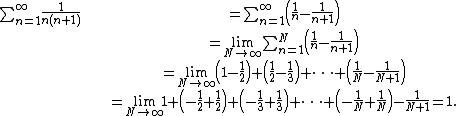
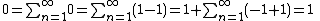
is not correct because this regrouping of terms is invalid unless the individual terms converge to 0; see Grandi's series. The way to avoid this error is to find the sum of the first N terms first and then take the limit as N approaches infinity:
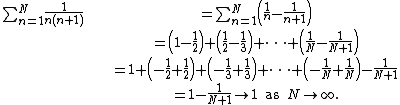
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a telescoping series is a series
Series (mathematics)
A series is the sum of the terms of a sequence. Finite sequences and series have defined first and last terms, whereas infinite sequences and series continue indefinitely....
whose partial sums eventually only have a fixed number of terms after cancellation. Such a technique is also known as the method of differences.
For example, the series
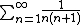
simplifies as
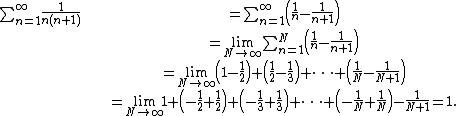
A pitfall
Although telescoping can be a useful technique, there are pitfalls to watch out for: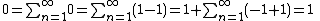
is not correct because this regrouping of terms is invalid unless the individual terms converge to 0; see Grandi's series. The way to avoid this error is to find the sum of the first N terms first and then take the limit as N approaches infinity:
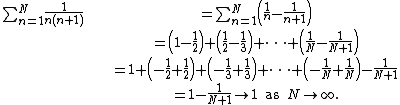
More examples
- Many trigonometric functionTrigonometric functionIn mathematics, the trigonometric functions are functions of an angle. They are used to relate the angles of a triangle to the lengths of the sides of a triangle...
s also admit representation as a difference, which allows telescopic cancelling between the consecutive terms.
-

- Some sums of the form
- where f and g are polynomial functions whose quotient may be broken up into partial fractionPartial fractionIn algebra, the partial fraction decomposition or partial fraction expansion is a procedure used to reduce the degree of either the numerator or the denominator of a rational function ....
s, will fail to admit summationSummationSummation is the operation of adding a sequence of numbers; the result is their sum or total. If numbers are added sequentially from left to right, any intermediate result is a partial sum, prefix sum, or running total of the summation. The numbers to be summed may be integers, rational numbers,...
by this method. In particular, we have
-
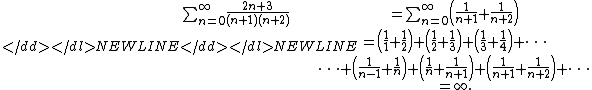
- The problem is that the terms do not cancel.
- Let k be a positive integer. Then
- where Hk is the kth harmonic number. All of the terms after 1/(k − 1) cancel.
An application in probability theory
In probability theoryProbability theoryProbability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, a Poisson processPoisson processA Poisson process, named after the French mathematician Siméon-Denis Poisson , is a stochastic process in which events occur continuously and independently of one another...
is a stochastic process of which the simplest case involves "occurrences" at random times, the waiting time until the next occurrence having a memorylessMemorylessnessIn probability and statistics, memorylessness is a property of certain probability distributions: the exponential distributions of non-negative real numbers and the geometric distributions of non-negative integers....
exponential distributionExponential distributionIn probability theory and statistics, the exponential distribution is a family of continuous probability distributions. It describes the time between events in a Poisson process, i.e...
, and the number of "occurrences" in any time interval having a Poisson distributionPoisson distributionIn probability theory and statistics, the Poisson distribution is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time and/or space if these events occur with a known average rate and independently of the time since...
whose expected value is proportional to the length of the time interval. Let Xt be the number of "occurrences" before time t, and let Tx be the waiting time until the xth "occurrence". We seek the probability density functionProbability density functionIn probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
of the random variableRandom variableIn probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
Tx. We use the probability mass functionProbability mass functionIn probability theory and statistics, a probability mass function is a function that gives the probability that a discrete random variable is exactly equal to some value...
for the Poisson distribution, which tells us that
where λ is the average number of occurrences in any time interval of length 1. Observe that the event [Xt ≥ x] is the same as the event [Tx ≤ t], and thus they have the same probability. The density function we seek is therefore
-
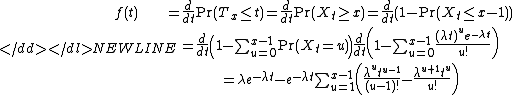
The sum telescopes, leaving
Other applications
For other applications, see:
- Grandi's series;
- Proof that the sum of the reciprocals of the primes diverges, where one of the proofs uses a telescoping sum;
- Order statisticOrder statisticIn statistics, the kth order statistic of a statistical sample is equal to its kth-smallest value. Together with rank statistics, order statistics are among the most fundamental tools in non-parametric statistics and inference....
, where a telescoping sum occurs in the derivation of a probability density function; - Lefschetz fixed-point theoremLefschetz fixed-point theoremIn mathematics, the Lefschetz fixed-point theorem is a formula that counts the fixed points of a continuous mapping from a compact topological space X to itself by means of traces of the induced mappings on the homology groups of X...
, where a telescoping sum arises in algebraic topologyAlgebraic topologyAlgebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
; - Homology theoryHomology theoryIn mathematics, homology theory is the axiomatic study of the intuitive geometric idea of homology of cycles on topological spaces. It can be broadly defined as the study of homology theories on topological spaces.-The general idea:...
, again in algebraic topology; - Eilenberg–Mazur swindleEilenberg–Mazur swindleIn mathematics, the Eilenberg–Mazur swindle, named after Samuel Eilenberg and Barry Mazur, is a method of proof that involves paradoxical properties of infinite sums. In geometric topology it was introduced by and is often called the Mazur swindle...
, where a telescoping sum of knots occurs.
-