
Geometric phase
Encyclopedia
In classical
and quantum mechanics
, the geometric phase, Pancharatnam–Berry phase (named after S. Pancharatnam
and Sir Michael Berry), Pancharatnam phase or most commonly Berry phase, is a phase
acquired over
the course of a cycle, when the system is subjected to cyclic adiabatic processes, which results from the geometrical properties of the parameter space
of the Hamiltonian
. The phenomenon was first discovered in 1956, and rediscovered in 1984. It can be seen in the Aharonov–Bohm effect and in the conical intersection
of potential energy surface
s. In the case of the Aharonov–Bohm effect, the adiabatic parameter is the magnetic field
inside the solenoid
, and cyclic means that the difference involved in measuring the effect by interference corresponds to a closed loop, in the usual way (see below). In the case of the conical intersection, the adiabatic parameters are the molecular coordinates
. Apart from quantum mechanics, it arises in a variety of other wave
systems, such as classical optics
. As a rule of thumb, it occurs whenever there are at least two parameters affecting a wave,
in the vicinity of some sort of singularity or some sort of hole in the topology.
Waves are characterized by amplitude
and phase
, and both may vary as a function of those parameters. The Berry phase occurs when both parameters are changed simultaneously but very slowly (adiabatically), and eventually brought back to the initial configuration. In quantum mechanics, this could e.g. involve rotations but also translations of particles, which are apparently undone at the end. Intuitively one expects that the waves in the system return to the initial state, as characterized by the amplitudes and phases (and accounting for the passage of time). However, if the parameter excursions correspond to a cyclic loop instead of a self-retracing back-and-forth variation, then it is possible that the initial and final states differ in their phases. This phase difference is the Berry phase, and its occurrence typically indicates that the system's parameter dependence is singular
(undefined) for some combination of parameters.
To measure
the Berry phase in a wave system, an interference experiment
is required. The Foucault pendulum
is an example from classical mechanics
that is sometimes used to illustrate the Berry phase. This mechanics analogue of the Berry phase is known as the Hannay angle
.
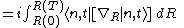
. An easy explanation in terms of geometric phases is given by von Bergmann and von Bergmann:
In summary, there are no inertial forces that could make the pendulum precess. Thus the orientation of the pendulum undergoes parallel transport
along the path of fixed latitude. By the Gauss–Bonnet theorem
the phase shift is given by the enclosed solid angle.
. Suppose the fiber traces out some path in space and the light exits the fiber in the same direction as it entered. Then compare the initial and final polarizations. In semiclassical approximation the fiber functions as a waveguide
and the momentum of the light is at all times tangent to the fiber. The polarization can be thought of as an orientation perpendicular to the momentum. As the fiber traces out its path, the momentum vector of the light traces out a path on the sphere in momentum space. The path is closed since initial and final directions of the light coincide, and the polarization is a vector tangent to the sphere. Going to momentum space is equivalent to taking the Gauss map
. There are no forces that could make the polarization turn, just the constraint to remain tangent to the sphere. Thus the polarization undergoes parallel transport and the phase shift is given by the enclosed solid angle (times the spin, which in case of light is 1).
The stochastic pump effect can be interpreted in terms of a geometric phase in evolution of the moment generating function of stochastic currents.
 matrix" defined by
matrix" defined by
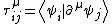
where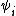 is the adiabatic electronic wave function, depending on the nuclear parameters
is the adiabatic electronic wave function, depending on the nuclear parameters 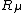 . The nonadiabatic coupling can be used to define a loop integral, analogous to the a Wigner loop (1974) in field theory, developed independently for molecular framework by M. Baer (1975, 1980, 2000). Given a closed loop
. The nonadiabatic coupling can be used to define a loop integral, analogous to the a Wigner loop (1974) in field theory, developed independently for molecular framework by M. Baer (1975, 1980, 2000). Given a closed loop 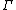 , parameterized by
, parameterized by 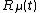 where
where 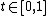 is a parameter and
is a parameter and  . The D-matrix is given by:
. The D-matrix is given by:
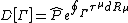
(here,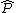 is a path ordering symbol). It can be shown that once
is a path ordering symbol). It can be shown that once  is large enough (i.e. a sufficient number of electronic states is considered) this matrix is diagonal with the diagonal elements equal to
is large enough (i.e. a sufficient number of electronic states is considered) this matrix is diagonal with the diagonal elements equal to  where
where 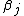 are the Berry phases associated with the loop for the
are the Berry phases associated with the loop for the 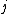 adiabatic electronic state.
adiabatic electronic state.
For time-reversal symmetrical electronic Hamiltonians the Berry phase reflects the number of conical intersections encircled by the loop. More accurately:
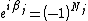
where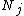 is the number of conical intersections involving the adiabatic state
is the number of conical intersections involving the adiabatic state  encircled by the loop
encircled by the loop 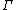 .
.
An alternative to the D-matrix approach would be a direct calculation of the Pancharatnam phase. This is especially useful if one is interested only in the Berry phases of a single adiabatic state. In this approach, one takes a number of points
of points 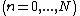 along the loop
along the loop 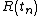 with
with 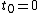 and
and 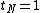 then using only the jth adiabatic states
then using only the jth adiabatic states 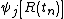 computes the Pancharatnam product of overlaps:
computes the Pancharatnam product of overlaps:
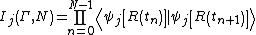
In the limit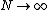 one has (See Ryb & Baer 2004 for explanation and some applications):
one has (See Ryb & Baer 2004 for explanation and some applications):
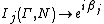
Classical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
and quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
, the geometric phase, Pancharatnam–Berry phase (named after S. Pancharatnam
S. Pancharatnam
Shivaramakrishnan Pancharatnam was an Indian physicist who did significant work in the field of optics. He is noted for his discovery of a type of geometric phase known as Pancharatnam phase for polarized beams passing through crystals....
and Sir Michael Berry), Pancharatnam phase or most commonly Berry phase, is a phase
Phase (waves)
Phase in waves is the fraction of a wave cycle which has elapsed relative to an arbitrary point.-Formula:The phase of an oscillation or wave refers to a sinusoidal function such as the following:...
acquired over
the course of a cycle, when the system is subjected to cyclic adiabatic processes, which results from the geometrical properties of the parameter space
Parameter space
In science, a parameter space is the set of values of parameters encountered in a particular mathematical model. Often the parameters are inputs of a function, in which case the technical term for the parameter space is domain of a function....
of the Hamiltonian
Hamiltonian (quantum mechanics)
In quantum mechanics, the Hamiltonian H, also Ȟ or Ĥ, is the operator corresponding to the total energy of the system. Its spectrum is the set of possible outcomes when one measures the total energy of a system...
. The phenomenon was first discovered in 1956, and rediscovered in 1984. It can be seen in the Aharonov–Bohm effect and in the conical intersection
Conical intersection
In quantum chemistry, a conical intersection of two potential energy surfaces of the same spatial and spin symmetries is the set of molecular geometry points where the two potential energy surfaces are degenerate . Conical intersections are ubiquitous in both trivial and non-trivial chemical...
of potential energy surface
Potential energy surface
A potential energy surface is generally used within the adiabatic or Born–Oppenheimer approximation in quantum mechanics and statistical mechanics to model chemical reactions and interactions in simple chemical and physical systems...
s. In the case of the Aharonov–Bohm effect, the adiabatic parameter is the magnetic field
Magnetic field
A magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;...
inside the solenoid
Solenoid
A solenoid is a coil wound into a tightly packed helix. In physics, the term solenoid refers to a long, thin loop of wire, often wrapped around a metallic core, which produces a magnetic field when an electric current is passed through it. Solenoids are important because they can create...
, and cyclic means that the difference involved in measuring the effect by interference corresponds to a closed loop, in the usual way (see below). In the case of the conical intersection, the adiabatic parameters are the molecular coordinates
Molecular geometry
Molecular geometry or molecular structure is the three-dimensional arrangement of the atoms that constitute a molecule. It determines several properties of a substance including its reactivity, polarity, phase of matter, color, magnetism, and biological activity.- Molecular geometry determination...
. Apart from quantum mechanics, it arises in a variety of other wave
Wave
In physics, a wave is a disturbance that travels through space and time, accompanied by the transfer of energy.Waves travel and the wave motion transfers energy from one point to another, often with no permanent displacement of the particles of the medium—that is, with little or no associated mass...
systems, such as classical optics
Optics
Optics is the branch of physics which involves the behavior and properties of light, including its interactions with matter and the construction of instruments that use or detect it. Optics usually describes the behavior of visible, ultraviolet, and infrared light...
. As a rule of thumb, it occurs whenever there are at least two parameters affecting a wave,
in the vicinity of some sort of singularity or some sort of hole in the topology.
Waves are characterized by amplitude
Amplitude
Amplitude is the magnitude of change in the oscillating variable with each oscillation within an oscillating system. For example, sound waves in air are oscillations in atmospheric pressure and their amplitudes are proportional to the change in pressure during one oscillation...
and phase
Phase (waves)
Phase in waves is the fraction of a wave cycle which has elapsed relative to an arbitrary point.-Formula:The phase of an oscillation or wave refers to a sinusoidal function such as the following:...
, and both may vary as a function of those parameters. The Berry phase occurs when both parameters are changed simultaneously but very slowly (adiabatically), and eventually brought back to the initial configuration. In quantum mechanics, this could e.g. involve rotations but also translations of particles, which are apparently undone at the end. Intuitively one expects that the waves in the system return to the initial state, as characterized by the amplitudes and phases (and accounting for the passage of time). However, if the parameter excursions correspond to a cyclic loop instead of a self-retracing back-and-forth variation, then it is possible that the initial and final states differ in their phases. This phase difference is the Berry phase, and its occurrence typically indicates that the system's parameter dependence is singular
Mathematical singularity
In mathematics, a singularity is in general a point at which a given mathematical object is not defined, or a point of an exceptional set where it fails to be well-behaved in some particular way, such as differentiability...
(undefined) for some combination of parameters.
To measure
Measurement
Measurement is the process or the result of determining the ratio of a physical quantity, such as a length, time, temperature etc., to a unit of measurement, such as the metre, second or degree Celsius...
the Berry phase in a wave system, an interference experiment
Experiment
An experiment is a methodical procedure carried out with the goal of verifying, falsifying, or establishing the validity of a hypothesis. Experiments vary greatly in their goal and scale, but always rely on repeatable procedure and logical analysis of the results...
is required. The Foucault pendulum
Foucault pendulum
The Foucault pendulum , or Foucault's pendulum, named after the French physicist Léon Foucault, is a simple device conceived as an experiment to demonstrate the rotation of the Earth. While it had long been known that the Earth rotated, the introduction of the Foucault pendulum in 1851 was the...
is an example from classical mechanics
Classical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
that is sometimes used to illustrate the Berry phase. This mechanics analogue of the Berry phase is known as the Hannay angle
Hannay angle
In classical mechanics, the Hannay angle is a mechanics analogue of the Berry phase. It was named after John Hannay of the University of Bristol, UK.-Example:...
.
Theory
In general the geometric phase is given by: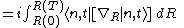
The Foucault pendulum
One of the easiest examples is the Foucault pendulumFoucault pendulum
The Foucault pendulum , or Foucault's pendulum, named after the French physicist Léon Foucault, is a simple device conceived as an experiment to demonstrate the rotation of the Earth. While it had long been known that the Earth rotated, the introduction of the Foucault pendulum in 1851 was the...
. An easy explanation in terms of geometric phases is given by von Bergmann and von Bergmann:
- How does the pendulum precess when it is taken around a general path C? For transport along the equator, the pendulum will not precess. [...] Now if C is made up of geodesicGeodesicIn mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...
segments, the precession will all come from the angles where the segments of the geodesics meet; the total precession is equal to the net deficit angle which in turn equals the solid angleSolid angleThe solid angle, Ω, is the two-dimensional angle in three-dimensional space that an object subtends at a point. It is a measure of how large that object appears to an observer looking from that point...
enclosed by C modulo 2π. Finally, we can approximate any loop by a sequence of geodesic segments, so the most general result (on or off the surface of the sphere) is that the net precession is equal to the enclosed solid angle.
In summary, there are no inertial forces that could make the pendulum precess. Thus the orientation of the pendulum undergoes parallel transport
Parallel transport
In geometry, parallel transport is a way of transporting geometrical data along smooth curves in a manifold. If the manifold is equipped with an affine connection , then this connection allows one to transport vectors of the manifold along curves so that they stay parallel with respect to the...
along the path of fixed latitude. By the Gauss–Bonnet theorem
Gauss–Bonnet theorem
The Gauss–Bonnet theorem or Gauss–Bonnet formula in differential geometry is an important statement about surfaces which connects their geometry to their topology...
the phase shift is given by the enclosed solid angle.
Polarized light in an optical fiber
A second example is linearly polarized light entering a single-mode optical fiberSingle-mode optical fiber
In fiber-optic communication, a single-mode optical fiber is an optical fiber designed to carry only a single ray of light . Modes are the possible solutions of the Helmholtz equation for waves, which is obtained by combining Maxwell's equations and the boundary conditions...
. Suppose the fiber traces out some path in space and the light exits the fiber in the same direction as it entered. Then compare the initial and final polarizations. In semiclassical approximation the fiber functions as a waveguide
Waveguide
A waveguide is a structure which guides waves, such as electromagnetic waves or sound waves. There are different types of waveguides for each type of wave...
and the momentum of the light is at all times tangent to the fiber. The polarization can be thought of as an orientation perpendicular to the momentum. As the fiber traces out its path, the momentum vector of the light traces out a path on the sphere in momentum space. The path is closed since initial and final directions of the light coincide, and the polarization is a vector tangent to the sphere. Going to momentum space is equivalent to taking the Gauss map
Gauss map
In differential geometry, the Gauss map maps a surface in Euclidean space R3 to the unit sphere S2. Namely, given a surface X lying in R3, the Gauss map is a continuous map N: X → S2 such that N is a unit vector orthogonal to X at p, namely the normal vector to X at p.The Gauss map can be defined...
. There are no forces that could make the polarization turn, just the constraint to remain tangent to the sphere. Thus the polarization undergoes parallel transport and the phase shift is given by the enclosed solid angle (times the spin, which in case of light is 1).
Stochastic pump effect
A stochastic pump is a classical stochastic system that responds with nonzero, on average, currents to periodic changes of parameters.The stochastic pump effect can be interpreted in terms of a geometric phase in evolution of the moment generating function of stochastic currents.
Exposing Berry/Pancharatnam phases in molecular adiabatic potential surface intersections
There are several ways to compute the Berry phase in molecules within the Born Oppenheimer framework. One way is through the "non-adiabatic coupling matrix" defined by
matrix" defined by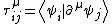
where
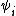 is the adiabatic electronic wave function, depending on the nuclear parameters
is the adiabatic electronic wave function, depending on the nuclear parameters 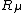 . The nonadiabatic coupling can be used to define a loop integral, analogous to the a Wigner loop (1974) in field theory, developed independently for molecular framework by M. Baer (1975, 1980, 2000). Given a closed loop
. The nonadiabatic coupling can be used to define a loop integral, analogous to the a Wigner loop (1974) in field theory, developed independently for molecular framework by M. Baer (1975, 1980, 2000). Given a closed loop 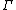 , parameterized by
, parameterized by 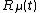 where
where 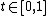 is a parameter and
is a parameter and  . The D-matrix is given by:
. The D-matrix is given by: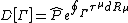
(here,
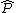 is a path ordering symbol). It can be shown that once
is a path ordering symbol). It can be shown that once  is large enough (i.e. a sufficient number of electronic states is considered) this matrix is diagonal with the diagonal elements equal to
is large enough (i.e. a sufficient number of electronic states is considered) this matrix is diagonal with the diagonal elements equal to  where
where 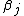 are the Berry phases associated with the loop for the
are the Berry phases associated with the loop for the 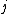 adiabatic electronic state.
adiabatic electronic state.For time-reversal symmetrical electronic Hamiltonians the Berry phase reflects the number of conical intersections encircled by the loop. More accurately:
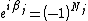
where
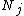 is the number of conical intersections involving the adiabatic state
is the number of conical intersections involving the adiabatic state  encircled by the loop
encircled by the loop 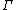 .
.An alternative to the D-matrix approach would be a direct calculation of the Pancharatnam phase. This is especially useful if one is interested only in the Berry phases of a single adiabatic state. In this approach, one takes a number
 of points
of points 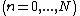 along the loop
along the loop 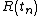 with
with 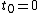 and
and 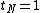 then using only the jth adiabatic states
then using only the jth adiabatic states 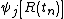 computes the Pancharatnam product of overlaps:
computes the Pancharatnam product of overlaps: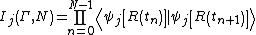
In the limit
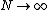 one has (See Ryb & Baer 2004 for explanation and some applications):
one has (See Ryb & Baer 2004 for explanation and some applications):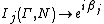
See also
- For the connection to mathematics, see curvature tensorCurvature tensorIn differential geometry, the term curvature tensor may refer to:* the Riemann curvature tensor of a Riemannian manifold — see also Curvature of Riemannian manifolds;* the curvature of an affine connection or covariant derivative ;...
, - Aharonov–Bohm effect,
- Conical intersectionConical intersectionIn quantum chemistry, a conical intersection of two potential energy surfaces of the same spatial and spin symmetries is the set of molecular geometry points where the two potential energy surfaces are degenerate . Conical intersections are ubiquitous in both trivial and non-trivial chemical...
s of potential energy surfacePotential energy surfaceA potential energy surface is generally used within the adiabatic or Born–Oppenheimer approximation in quantum mechanics and statistical mechanics to model chemical reactions and interactions in simple chemical and physical systems...
s. - Chern classChern classIn mathematics, in particular in algebraic topology and differential geometry, the Chern classes are characteristic classes associated to complex vector bundles.Chern classes were introduced by .-Basic idea and motivation:...
- Wilson loopWilson loopIn gauge theory, a Wilson loop is a gauge-invariant observable obtained from the holonomy of the gauge connection around a given loop...
- Winding numberWinding numberIn mathematics, the winding number of a closed curve in the plane around a given point is an integer representing the total number of times that curve travels counterclockwise around the point...
- Hannay angleHannay angleIn classical mechanics, the Hannay angle is a mechanics analogue of the Berry phase. It was named after John Hannay of the University of Bristol, UK.-Example:...

