One hundred million is the natural number

Natural number

In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...

 following 99999999 and preceding 100000001.

List of numbers – Integers 10000000 10000000 (number) Ten million is the natural number following 9999999 and preceding 10000001.In scientific notation, it is written as 107.In South Asia, it is known as the Crore.- Selected 8-digit numbers :*10077696 = 69...  100000000 1000000000 1000000000 (number) 1,000,000,000 is the natural number following 999,999,999 and preceding 1,000,000,001.In scientific notation, it is written as 109....
Cardinal Cardinal number In mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite...	One hundred million
Ordinal Ordinal number In set theory, an ordinal number, or just ordinal, is the order type of a well-ordered set. They are usually identified with hereditarily transitive sets. Ordinals are an extension of the natural numbers different from integers and from cardinals...	One hundred millionth
Factorization Factorization In mathematics, factorization or factoring is the decomposition of an object into a product of other objects, or factors, which when multiplied together give the original...	28 · 58
Binary Binary numeral system The binary numeral system, or base-2 number system, represents numeric values using two symbols, 0 and 1. More specifically, the usual base-2 system is a positional notation with a radix of 2...	101111101011110000100000000
Hexadecimal Hexadecimal In mathematics and computer science, hexadecimal is a positional numeral system with a radix, or base, of 16. It uses sixteen distinct symbols, most often the symbols 0–9 to represent values zero to nine, and A, B, C, D, E, F to represent values ten to fifteen...	5F5E100

In scientific notation

Scientific notation

Scientific notation is a way of writing numbers that are too large or too small to be conveniently written in standard decimal notation. Scientific notation has a number of useful properties and is commonly used in calculators and by scientists, mathematicians, doctors, and engineers.In scientific...

, it is written as 10⁸.

East Asian languages treat 100,000,000 as a counting unit, significant as the square of a myriad

Myriad

Myriad , "numberlesscountless, infinite", is a classical Greek word for the number 10,000. In modern English, the word refers to an unspecified large quantity.-History and usage:...

, also a counting unit. In Chinese, Japanese, and Korean respectively it is yì (億) (or wànwàn [萬萬] in ancient texts), oku (億), and eok (억/億). These languages do not have single words for a thousand to the second, third, fifth power, etc.)

Selected 9-digit numbers (100000001–999999999)

• 102334155 – Fibonacci number
  Fibonacci number
  In mathematics, the Fibonacci numbers are the numbers in the following integer sequence:0,\;1,\;1,\;2,\;3,\;5,\;8,\;13,\;21,\;34,\;55,\;89,\;144,\; \ldots\; ....
  
  
• 107890609 – Wedderburn-Etherington number
  Wedderburn-Etherington number
  In graph theory, the Wedderburn–Etherington numbers, named for Ivor Malcolm Haddon Etherington and Joseph Wedderburn, count how many weak binary trees can be constructed: that is, the number of trees for which each graph vertex is adjacent to no more than three other such vertices, for a...
  
  
• 111111111 – repunit
  Repunit
  In recreational mathematics, a repunit is a number like 11, 111, or 1111 that contains only the digit 1. The term stands for repeated unit and was coined in 1966 by Albert H. Beiler...
  
  , square root of 12345678987654321
• 111111113 – Chen prime
  Chen prime
  A prime number p is called a Chen prime if p + 2 is either a prime or a product of two primes. The even number 2p + 2 therefore satisfies Chen's theorem....
  
  , Sophie Germain prime
  Sophie Germain prime
  In number theory, a prime number p is a Sophie Germain prime if 2p + 1 is also prime. For example, 23 is a Sophie Germain prime because it is a prime and 2 × 23 + 1 = 47, and 47 is also a prime number...
  
  , cousin prime
  Cousin prime
  In mathematics, cousin primes are prime numbers that differ by four; compare this with twin primes, pairs of prime numbers that differ by two, and sexy primes, pairs of prime numbers that differ by six....
  
  .
• 123456789 – smallest zeroless base 10 pandigital number
  Pandigital number
  In mathematics, a pandigital number is an integer that in a given base has among its significant digits each digit used in the base at least once. For example, 1223334444555567890 is a pandigital number in base 10...
  
  
• 129140163 = 3¹⁷
• 129644790 – Catalan number
  Catalan number
  In combinatorial mathematics, the Catalan numbers form a sequence of natural numbers that occur in various counting problems, often involvingrecursively defined objects...
  
  
• 134217728 = 2²⁷
• 139854276 – the smallest pandigital square
• 142547559 – Motzkin number
  Motzkin number
  In mathematics, a Motzkin number for a given number n is the number of different ways of drawing non-intersecting chords on a circle between n points. The Motzkin numbers have very diverse applications in geometry, combinatorics and number theory...
  
  
• 165580141 – Fibonacci number
  Fibonacci number
  In mathematics, the Fibonacci numbers are the numbers in the following integer sequence:0,\;1,\;1,\;2,\;3,\;5,\;8,\;13,\;21,\;34,\;55,\;89,\;144,\; \ldots\; ....
  
  
• 179424673 – 10000000th prime number
  Prime number
  A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
  
  
• 190899322 – Bell number
  Bell number
  In combinatorics, the nth Bell number, named after Eric Temple Bell, is the number of partitions of a set with n members, or equivalently, the number of equivalence relations on it...
  
  
• 214358881 = 11⁸
• 222222222 – repdigit
  Repdigit
  In recreational mathematics, a repdigit is a natural number composed of repeated instances of the same digit, most often in the decimal numeral system....
  
  
• 222222227 – safe prime
  Safe prime
  A safe prime is a prime number of the form 2p + 1, where p is also a prime. The first few safe primes are...
  
  
• 225058681 – Pell number
  Pell number
  In mathematics, the Pell numbers are an infinite sequence of integers that have been known since ancient times, the denominators of the closest rational approximations to the square root of 2. This sequence of approximations begins 1/1, 3/2, 7/5, 17/12, and 41/29, so the sequence of Pell numbers...
  
  
• 225331713 – self-descriptive number
  Self-descriptive number
  A self-descriptive number is an integer m that in a given base b is b-digits long in which each digit d at position n counts how many instances of digit n are in m.For example, in base 10, the number 6210001000 is self-descriptive because of the following...
  
   in base 9
• 244140625 = 5¹¹
• 253450711 – Wedderburn-Etherington number
• 267914296 – Fibonacci number
  Fibonacci number
  In mathematics, the Fibonacci numbers are the numbers in the following integer sequence:0,\;1,\;1,\;2,\;3,\;5,\;8,\;13,\;21,\;34,\;55,\;89,\;144,\; \ldots\; ....
  
  
• 268402687 – Carol number
• 268435456 = 2²⁸
• 268468223 – Kynea number
• 272400600 – the number of terms of the harmonic series
  Harmonic series (mathematics)
  In mathematics, the harmonic series is the divergent infinite series:Its name derives from the concept of overtones, or harmonics in music: the wavelengths of the overtones of a vibrating string are 1/2, 1/3, 1/4, etc., of the string's fundamental wavelength...
  
   required to pass 20
• 275305224 – the number of magic square
  Magic square
  In recreational mathematics, a magic square of order n is an arrangement of n2 numbers, usually distinct integers, in a square, such that the n numbers in all rows, all columns, and both diagonals sum to the same constant. A normal magic square contains the integers from 1 to n2...
  
  s of order 5, excluding rotations and reflections
• 282475249 = 7¹⁰
• 333333333 – repdigit
• 367567200 – colossally abundant number
  Colossally abundant number
  In mathematics, a colossally abundant number is a natural number that, in some rigorous sense, has a lot of divisors...
  
  
• 381654729 – the only polydivisible number
  Polydivisible number
  In mathematics a polydivisible number is a number with digits abcde... that has the following properties :# Its first digit a is not 0.# The number formed by its first two digits ab is a multiple of 2....
  
   that is also a zeroless pandigital number
  Pandigital number
  In mathematics, a pandigital number is an integer that in a given base has among its significant digits each digit used in the base at least once. For example, 1223334444555567890 is a pandigital number in base 10...
  
  
• 387420489 = 3¹⁸, 9⁹ and in tetration
  Tetration
  In mathematics, tetration is an iterated exponential and is the next hyper operator after exponentiation. The word tetration was coined by English mathematician Reuben Louis Goodstein from tetra- and iteration. Tetration is used for the notation of very large numbers...
  
   notation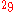
• 400763223 – Motzkin number
• 433494437 – Fibonacci number
  Fibonacci number
  In mathematics, the Fibonacci numbers are the numbers in the following integer sequence:0,\;1,\;1,\;2,\;3,\;5,\;8,\;13,\;21,\;34,\;55,\;89,\;144,\; \ldots\; ....
  
  
• 442386619 – alternating factorial
  Alternating factorial
  In mathematics, an alternating factorial is the absolute value of the alternating sum of the first n factorials.This is the same as their sum, with the odd-indexed factorials multiplied by −1 if n is even, and the even-indexed factorials multiplied by −1 if n is odd, resulting in an...
  
  
• 444444444 – repdigit
  Repdigit
  In recreational mathematics, a repdigit is a natural number composed of repeated instances of the same digit, most often in the decimal numeral system....
  
  
• 477638700 – Catalan number
• 479001599 – factorial prime
  Factorial prime
  A factorial prime is a prime number that is one less or one more than a factorial . The first few factorial primes are:n! − 1 is prime for :n! + 1 is prime for :...
  
  
• 479001600 = 12!
• 536870912 = 2²⁹
• 543339720 – Pell number
• 554999445 – 9-digit analogue to Kaprekar constant
• 555555555 – repdigit
  Repdigit
  In recreational mathematics, a repdigit is a natural number composed of repeated instances of the same digit, most often in the decimal numeral system....
  
  
• 596572387 – Wedderburn-Etherington number
• 666666666 – repdigit
  Repdigit
  In recreational mathematics, a repdigit is a natural number composed of repeated instances of the same digit, most often in the decimal numeral system....
  
  
• 701408733 – Fibonacci number
  Fibonacci number
  In mathematics, the Fibonacci numbers are the numbers in the following integer sequence:0,\;1,\;1,\;2,\;3,\;5,\;8,\;13,\;21,\;34,\;55,\;89,\;144,\; \ldots\; ....
  
  
• 715827883 – Wagstaff prime
• 777777777 – repdigit
  Repdigit
  In recreational mathematics, a repdigit is a natural number composed of repeated instances of the same digit, most often in the decimal numeral system....
  
  
• 815730721 = 13⁸
• 888888888 – repdigit
  Repdigit
  In recreational mathematics, a repdigit is a natural number composed of repeated instances of the same digit, most often in the decimal numeral system....
  
  
• 906150257 – smallest counterexample to the Polya conjecture
  Pólya conjecture
  In number theory, the Pólya conjecture stated that 'most' of the natural numbers less than any given number have an odd number of prime factors. The conjecture was posited by the Hungarian mathematician George Pólya in 1919, and proved false in 1958...
  
  
• 987654321 – largest zeroless pandigital number
• 999999937 – largest 9-digit prime
• 999999999 – repdigit
  Repdigit
  In recreational mathematics, a repdigit is a natural number composed of repeated instances of the same digit, most often in the decimal numeral system....