Repunit
Encyclopedia
In recreational mathematics
, a repunit is a number
like 11, 111, or 1111 that contains only the digit 1. The term stands for repeated unit and was coined in 1966 by Albert H. Beiler. A repunit prime is a repunit that is also a prime number
.
Thus, the number Rn(b) consists of n copies of the digit 1 in base b representation. The first two repunits base b for n=1 and n=2 are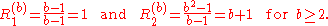
In particular, the decimal
(base-10) repunits that are often referred to as simply repunits are defined as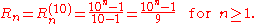
Thus, the number Rn = Rn(10) consists of n copies of the digit 1 in base 10 representation. The sequence of repunits base 10 starts with
Similarly, the repunits base 2 are defined as
Thus, the number Rn(2) consists of n copies of the digit 1 in base 2 representation. In fact, the base-2 repunits are the well-respected Mersenne number
s Mn = 2n − 1.
of such numbers.
It is easy to show that if n is divisible by a, then Rn(b) is divisible by Ra(b):
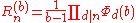
where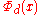
is the 
cyclotomic polynomial
and d ranges over the divisors of n. For p prime,
, which has the expected form of a repunit when x is substituted with b.
For example, 9 is divisible by 3, and thus R9 is divisible by R3—in fact, 111111111 = 111 · 1001001. The corresponding cyclotomic polynomials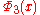
and 
are 
and 
respectively. Thus, for Rn to be prime n must necessarily be prime.
But it is not sufficient for n to be prime; for example, R3 = 111 = 3 · 37 is not prime. Except for this case of R3, p can only divide Rn for prime n if p = 2kn + 1 for some k.
. On April 3, 2007 Harvey Dubner
(who also found R49081) announced that R109297 is a probable prime. He later announced there are no others from R86453 to R200000. On July 15, 2007 Maksym Voznyy announced R270343 to be probably prime, along with his intent to search to 400000. As of September 2010, all further candidates up to R1300000 have been tested, but no new probable primes have been found so far.
It has been conjectured that there are infinitely many repunit primes and they seem to occur roughly as often as the prime number theorem
would predict: the exponent of the Nth repunit prime is generally around a fixed multiple of the exponent of the (N-1)th.
The prime repunits are a trivial subset of the permutable prime
s, i.e., primes that remain prime after any permutation
of their digits.
s.
corresponding to
of
). 
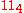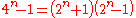, and 3 always divides 
when n is odd and 
when n is even. For n greater than 2, both 
and 
are greater than 3, so removing the factor of 3 still leaves two factors greater than 1, so the number cannot be prime.
) repunit primes are
corresponding to
of
corresponding to
of
corresponding to
of
or base-9
repunit prime is 73
(
). 
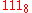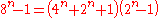, and 7 divides 
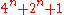when n is not divisible by 3 and 
when n is a multiple of 3. 
, and 2 always divides both 
and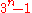 
.
s are for
of
The first three of these in decimal are
It was found very early on that for any prime p greater than 5, the period
of the decimal expansion of 1/p is equal to the length of the smallest repunit number that is divisible by p. Tables of the period of reciprocal of primes up to 60,000 had been published by 1860 and permitted the factorization
by such mathematicians as Reuschle of all repunits up to R16 and many larger ones. By 1880, even R17 had been factored and it is curious that, though Édouard Lucas
showed no prime below three million had period nineteen, there was no attempt to test any repunit for primality until early in the twentieth century. The American mathematician Oscar Hoppe proved R19 to be prime in 1916 and Lehmer and Kraitchik independently found R23 to be prime in 1929.
Further advances in the study of repunits did not occur until the 1960s, when computers allowed many new factors of repunits to be found and the gaps in earlier tables of prime periods corrected. R317 was found to be a probable prime
circa 1966 and was proved prime eleven years later, when R1031 was shown to be the only further possible prime repunit with fewer than ten thousand digits. It was proven prime in 1986, but searches for further prime repunits in the following decade consistently failed. However, there was a major side-development in the field of generalized repunits, which produced a large number of new primes and probable primes.
Since 1999, four further probably prime repunits have been found, but it is unlikely that any of them will be proven prime in the foreseeable future because of their huge size.
The Cunningham project
endeavours to document the integer factorizations of (among other numbers) the repunits to base 2, 3, 5, 6, 7, 10, 11, and 12.
Recreational mathematics
Recreational mathematics is an umbrella term, referring to mathematical puzzles and mathematical games.Not all problems in this field require a knowledge of advanced mathematics, and thus, recreational mathematics often attracts the curiosity of non-mathematicians, and inspires their further study...
, a repunit is a number
Number
A number is a mathematical object used to count and measure. In mathematics, the definition of number has been extended over the years to include such numbers as zero, negative numbers, rational numbers, irrational numbers, and complex numbers....
like 11, 111, or 1111 that contains only the digit 1. The term stands for repeated unit and was coined in 1966 by Albert H. Beiler. A repunit prime is a repunit that is also a prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
.
Definition
The base-b repunits are defined asThus, the number Rn(b) consists of n copies of the digit 1 in base b representation. The first two repunits base b for n=1 and n=2 are
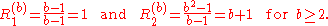
In particular, the decimal
Decimal
The decimal numeral system has ten as its base. It is the numerical base most widely used by modern civilizations....
(base-10) repunits that are often referred to as simply repunits are defined as
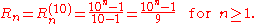
Thus, the number Rn = Rn(10) consists of n copies of the digit 1 in base 10 representation. The sequence of repunits base 10 starts with
- 1, 1111 (number)11 is the natural number following 10 and preceding 12.Eleven is the first number which cannot be counted with a human's eight fingers and two thumbs additively. In English, it is the smallest positive integer requiring three syllables and the largest prime number with a single-morpheme name...
, 111111 (number)111 is the natural number following 110 and preceding 112. It is the lowest positive integer requiring six syllables to name in American English, or seven syllables in Canadian and British English...
, 1111, ... .
Similarly, the repunits base 2 are defined as
Thus, the number Rn(2) consists of n copies of the digit 1 in base 2 representation. In fact, the base-2 repunits are the well-respected Mersenne number
Mersenne prime
In mathematics, a Mersenne number, named after Marin Mersenne , is a positive integer that is one less than a power of two: M_p=2^p-1.\,...
s Mn = 2n − 1.
Properties
- Any repunit in any base having a composite number of digits is necessarily composite. Only repunits (in any base) having a prime number of digits might be prime (necessary but not sufficient condition). For example,
- R35(b) = 11111111111111111111111111111111111 = 11111 × 1000010000100001000010000100001 = 1111111 × 10000001000000100000010000001,
- since 35 = 7 × 5 = 5 × 7. This repunit factorization does not depend on the base b in which the repunit is expressed.
- Any positive multiple of the repunit Rn(b) contains at least n nonzero digits in base b.
- The only known numbers that are repunits with at least 3 digits in more than one base simultaneously are 31 (111 in base 5, 11111 in base 2) and 8191 (111 in base 90, 1111111111111 in base 2). The Goormaghtigh conjectureGoormaghtigh conjectureIn mathematics, the Goormaghtigh conjecture is a conjecture in number theory named for the Belgian mathematician René Goormaghtigh. The conjecture is that the only non-trivial integer solutions of the exponential Diophantine equation...
says there are only these two cases.
- It is easy to prove that given n, such that n is not exactly divisible by 2 or p, there exists a repunit in base 2p that is a multiple of n.
Factorization of decimal repunits
|
|
Repunit primes
The definition of repunits was motivated by recreational mathematicians looking for prime factorsInteger factorization
In number theory, integer factorization or prime factorization is the decomposition of a composite number into smaller non-trivial divisors, which when multiplied together equal the original integer....
of such numbers.
It is easy to show that if n is divisible by a, then Rn(b) is divisible by Ra(b):
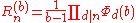
where
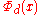is the cyclotomic polynomialCyclotomic polynomial
In algebra, the nth cyclotomic polynomial, for any positive integer n, is the monic polynomial:\Phi_n = \prod_\omega \,where the product is over all nth primitive roots of unity ω in a field, i.e...
and d ranges over the divisors of n. For p prime,
, which has the expected form of a repunit when x is substituted with b.For example, 9 is divisible by 3, and thus R9 is divisible by R3—in fact, 111111111 = 111 · 1001001. The corresponding cyclotomic polynomials
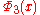and are and respectively. Thus, for Rn to be prime n must necessarily be prime.But it is not sufficient for n to be prime; for example, R3 = 111 = 3 · 37 is not prime. Except for this case of R3, p can only divide Rn for prime n if p = 2kn + 1 for some k.
Decimal repunit primes
Rn is prime for n = 2, 19, 23, 317, 1031,... (sequence A004023 in OEIS). R49081 and R86453 are probably primeProbable prime
In number theory, a probable prime is an integer that satisfies a specific condition also satisfied by all prime numbers. Different types of probable primes have different specific conditions...
. On April 3, 2007 Harvey Dubner
Harvey Dubner
Harvey Dubner is a semi-retired engineer living in New Jersey, noted for his contributions to finding large prime numbers. In 1984, he and his son Robert collaborated in developing the 'Dubner cruncher', a board which used a commercial finite impulse response filter chip to speed up dramatically...
(who also found R49081) announced that R109297 is a probable prime. He later announced there are no others from R86453 to R200000. On July 15, 2007 Maksym Voznyy announced R270343 to be probably prime, along with his intent to search to 400000. As of September 2010, all further candidates up to R1300000 have been tested, but no new probable primes have been found so far.
It has been conjectured that there are infinitely many repunit primes and they seem to occur roughly as often as the prime number theorem
Prime number theorem
In number theory, the prime number theorem describes the asymptotic distribution of the prime numbers. The prime number theorem gives a general description of how the primes are distributed amongst the positive integers....
would predict: the exponent of the Nth repunit prime is generally around a fixed multiple of the exponent of the (N-1)th.
The prime repunits are a trivial subset of the permutable prime
Permutable prime
A permutable prime is a prime number, which, in a given base, can have its digits' positions switched through any permutation and still spell a prime number. H. E...
s, i.e., primes that remain prime after any permutation
Permutation
In mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
of their digits.
Base-2 repunit primes
Base-2 repunit primes are called Mersenne primeMersenne prime
In mathematics, a Mersenne number, named after Marin Mersenne , is a positive integer that is one less than a power of two: M_p=2^p-1.\,...
s.
Base-3 repunit primes
The first few base-3 repunit primes are- 13, 1093, 797161, 3754733257489862401973357979128773, 6957596529882152968992225251835887181478451547013, ... ,
corresponding to
of
- 3, 7, 13, 71, 103, ... .
Base-4 repunit primes
The only base-4 repunit prime is 5 (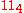). 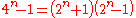, and 3 always divides when n is odd and when n is even. For n greater than 2, both and are greater than 3, so removing the factor of 3 still leaves two factors greater than 1, so the number cannot be prime.Base 5 repunit primes
The first few base-5 (quinaryQuinary
Quinary is a numeral system with five as the base. A possible origination of a quinary system is that there are five fingers on either hand. The base five is stated from 0-4...
) repunit primes are
- 31, 19531, 12207031, 305175781, 177635683940025046467781066894531,
corresponding to
of
- 3, 7, 11, 13, 47, ... .
Base 6 repunit primes
The first few base-6 repunit primes are- 7, 43, 55987, 7369130657357778596659, 3546245297457217493590449191748546458005595187661976371, ...,
corresponding to
of
- 2, 3, 7, 29, 71, ...
Base 7 repunit primes
The first few base 7 repunit primes are- 2801, 16148168401, 85053461164796801949539541639542805770666392330682673302530819774105141531698707146930307290253537320447270457,
138502212710103408700774381033135503926663324993317631729227790657325163310341833227775945426052637092067324133850503035623601
corresponding to
of
- 5, 13, 131, 149, ...
Base 8 and 9 repunit primes
The only base-8Octal
The octal numeral system, or oct for short, is the base-8 number system, and uses the digits 0 to 7. Numerals can be made from binary numerals by grouping consecutive binary digits into groups of three...
or base-9
Nonary
Nonary is a base- numeral system, typically using the digits 0-8, but not the digit 9.The first few numbers in nonary and decimal are:Nonary 1 2 3 4 5 6 7 81011121314Decimal 1 2 3 4 5 6 7 8 910111213The...
repunit prime is 73
73 (number)
73 is the natural number following 72 and preceding 74. In English, it is the smallest integer with twelve letters in its spelled out name.- In mathematics :...
(
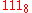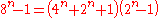). , and 7 divides 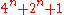when n is not divisible by 3 and when n is a multiple of 3. , and 2 always divides both and 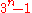.Base 20 (vigesimal) repunit primes
The only known vigesimal (base 20) repunit primes or probable primeProbable prime
In number theory, a probable prime is an integer that satisfies a specific condition also satisfied by all prime numbers. Different types of probable primes have different specific conditions...
s are for
of
- 3, 11, 17, 1487, 31013, 48859, 61403
The first three of these in decimal are
- 421, 10778947368421 and 689852631578947368421
History
Although they were not then known by that name, repunits in base 10 were studied by many mathematicians during the nineteenth century in an effort to work out and predict the cyclic patterns of recurring decimals.It was found very early on that for any prime p greater than 5, the period
Repeating decimal
In arithmetic, a decimal representation of a real number is called a repeating decimal if at some point it becomes periodic, that is, if there is some finite sequence of digits that is repeated indefinitely...
of the decimal expansion of 1/p is equal to the length of the smallest repunit number that is divisible by p. Tables of the period of reciprocal of primes up to 60,000 had been published by 1860 and permitted the factorization
Integer factorization
In number theory, integer factorization or prime factorization is the decomposition of a composite number into smaller non-trivial divisors, which when multiplied together equal the original integer....
by such mathematicians as Reuschle of all repunits up to R16 and many larger ones. By 1880, even R17 had been factored and it is curious that, though Édouard Lucas
Edouard Lucas
François Édouard Anatole Lucas was a French mathematician. Lucas is known for his study of the Fibonacci sequence. The related Lucas sequences and Lucas numbers are named after him.-Biography:...
showed no prime below three million had period nineteen, there was no attempt to test any repunit for primality until early in the twentieth century. The American mathematician Oscar Hoppe proved R19 to be prime in 1916 and Lehmer and Kraitchik independently found R23 to be prime in 1929.
Further advances in the study of repunits did not occur until the 1960s, when computers allowed many new factors of repunits to be found and the gaps in earlier tables of prime periods corrected. R317 was found to be a probable prime
Probable prime
In number theory, a probable prime is an integer that satisfies a specific condition also satisfied by all prime numbers. Different types of probable primes have different specific conditions...
circa 1966 and was proved prime eleven years later, when R1031 was shown to be the only further possible prime repunit with fewer than ten thousand digits. It was proven prime in 1986, but searches for further prime repunits in the following decade consistently failed. However, there was a major side-development in the field of generalized repunits, which produced a large number of new primes and probable primes.
Since 1999, four further probably prime repunits have been found, but it is unlikely that any of them will be proven prime in the foreseeable future because of their huge size.
The Cunningham project
Cunningham project
The Cunningham project aims to find factors of large numbers of the formb^n \pm 1for b = 2, 3, 5, 6, 7, 10, 11, 12 and large exponents n. The project is named after Allan Joseph Champneys Cunningham, who published the first version of the table together with Herbert J. Woodall in 1925...
endeavours to document the integer factorizations of (among other numbers) the repunits to base 2, 3, 5, 6, 7, 10, 11, and 12.
See also
- RepdigitRepdigitIn recreational mathematics, a repdigit is a natural number composed of repeated instances of the same digit, most often in the decimal numeral system....
- Recurring decimal
- All one polynomialAll one polynomialAn all one polynomial is a polynomial used in finite fields, specifically GF . The AOP is a 1-equally spaced polynomial.An AOP of degree m has all terms from xm to x0 with coefficients of 1, and can be written as...
- Another generalization - Goormaghtigh conjectureGoormaghtigh conjectureIn mathematics, the Goormaghtigh conjecture is a conjecture in number theory named for the Belgian mathematician René Goormaghtigh. The conjecture is that the only non-trivial integer solutions of the exponential Diophantine equation...
Web sites
- The main tables of the Cunningham project.
- Repunit at The Prime Pages by Chris Caldwell.
- Repunits and their prime factors at World!Of Numbers.
- Prime generalized repunits of at least 1000 decimal digits by Andy Steward
- Repunit Primes Project Giovanni Di Maria's repunit primes page.
- The Repunit Primes Project
- Factorizations of 11...11 (Repunit) by Makoto Kamada
Books
- S. Yates, Repunits and repetends. ISBN 0-9608652-0-9.
- A. Beiler, Recreations in the theory of numbers. ISBN 0-486-21096-0. Chapter 11, of course.
- Paulo RibenboimPaulo RibenboimPaulo Ribenboim is a mathematician who specializes in number theory. Ribenboim was born in Recife, Brazil, and has lived in Canada since 1962. He has authored 13 books and 120 articles...
, The New Book Of Prime Number Records. ISBN 0-387-94457-5.